代码随想录算法训练营第十七天| 110 平衡二叉树 257 二叉树的所有路径 404 左子叶之和
目录
110 平衡二叉树
求深度:前序遍历
求高度:后序遍历
递归
class Solution {
public boolean isBalanced(TreeNode root) {
if(traversal(root) == -1)return false;
return true;
}
//后序遍历求高度
private int traversal(TreeNode root){
if(root == null)return 0;
int left = traversal(root.left);
if(left == -1)return -1;
int right = traversal(root.right);
if(right == -1)return -1;
if(Math.abs(left - right) > 1)return -1;
return 1 + Math.max(left,right);//返回整个子树的最大值
}
}时间复杂度O(n)
空间复杂度O(n)
迭代
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
while (root!= null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
TreeNode cur = stack.peek();
// 右结点为null或已经遍历过
if (cur.right == null || cur.right == pre) {
// 比较左右子树的高度差,输出
if (Math.abs(getHeight(cur.left) - getHeight(cur.right)) > 1) {
return false;
}
stack.pop();
pre = cur;
root = null;// 当前结点下,没有要遍历的结点了
} else {
root = cur.right;// 右结点还没遍历,遍历右结点
}
}
return true;
}
public int getHeight(TreeNode root) {
if(root == null)return 0;
Deque<TreeNode>st = new LinkedList<>();
int depth = 0;
st.offer(root);
while(!st.isEmpty()){
int siz = st.size();
depth++;
for(int i = 0;i < siz;i++){
TreeNode cur = st.poll();
if(cur.left != null)st.offer(cur.left);
if(cur.right != null)st.offer(cur.right);
}
}
return depth;
}
}时间复杂度O(n^2)
空间复杂度O(n^2)
257 二叉树的所有路径
递归
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String>res = new ArrayList<>();
List<Integer>nums = new ArrayList<>();
traversal(root,res,nums);
return res;
}
private void traversal(TreeNode root,List<String>res,List<Integer>nums){
//前序遍历 中左右
nums.add(root.val);
//达到子节点,将结果加入到res中
if(root.left == null && root.right == null){
StringBuilder sb = new StringBuilder();
for(int i = 0;i < nums.size() - 1;i++){
sb.append(nums.get(i)).append("->");
}
sb.append(nums.get(nums.size() - 1));
res.add(sb.toString());
return;
}
//左
if(root.left != null){
traversal(root.left,res,nums);//递归
nums.remove(nums.size() - 1);//回溯
}
//右
if(root.right != null){
traversal(root.right,res,nums);
nums.remove(nums.size() - 1);
}
}
}时间复杂度O(n^2)
空间复杂度O(n^2)
迭代
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String>res = new ArrayList<>();
if(root == null)return res;
Deque<Object>st = new LinkedList<>();
st.push(root);
st.push(root.val + "");
while(!st.isEmpty()){
String str = (String)st.poll();
TreeNode cur = (TreeNode)st.poll();
if(cur.left == null && cur.right == null){
res.add(str);
continue;
}
if(cur.left != null){
st.push(cur.left);
st.push(str + "->" + cur.left.val);
}
if(cur.right != null){
st.push(cur.right);
st.push(str + "->" + cur.right.val);
}
}
return res;
}
}时间复杂度O(n^2)
空间复杂度O(n^2)
404 左子叶之和
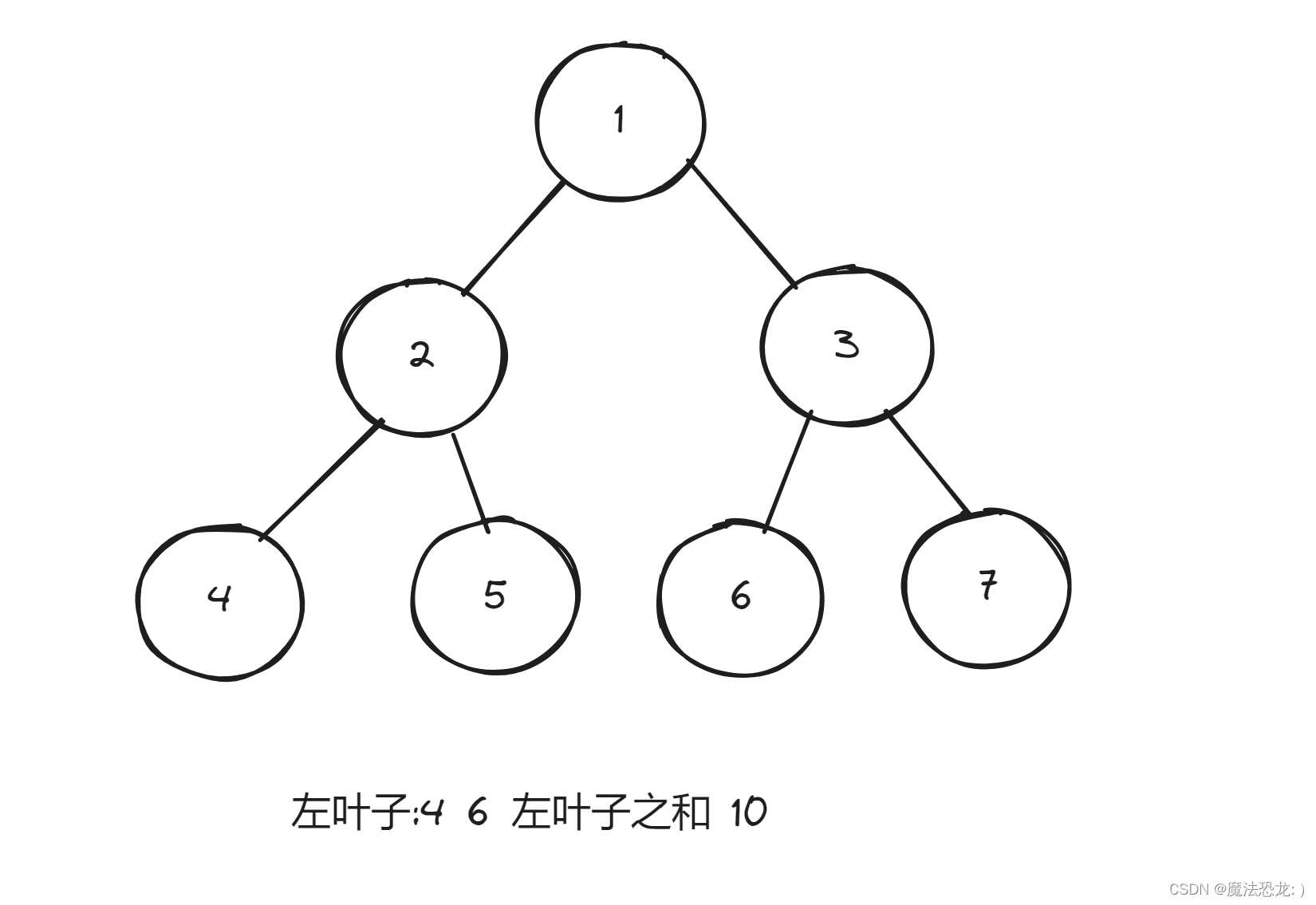
递归
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
return traversal(root);
}
private int traversal(TreeNode root){
if(root == null)return 0;
if(root.left == null && root.right == null)return 0;
int sum = 0;
if(root.left != null && root.left.left == null && root.left.right == null)sum += root.left.val;//如果该子树下有左叶子节点,将其val加入到sum中
sum += traversal(root.left);//加上其左子树下的左叶子之和
sum += traversal(root.right);//加上其右子树下的左叶子节点之和
return sum;
}
}时间复杂度O(n)
空间复杂度O(n)为所开栈空间的大小,最坏情况下二叉树呈链状,此时为O(n)
迭代
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if(root == null)return 0;
Deque<TreeNode>st = new LinkedList<>();
st.push(root);
int res = 0;
while(!st.isEmpty()){
TreeNode node = st.pop();
if(node.left != null && node.left.left == null && node.left.right == null)res += node.left.val;
if(node.right != null)st.add(node.right);
if(node.left != null)st.add(node.left);
}
return res;
}
}时间复杂度O(n)
空间复杂度O(n)
层序遍历迭代法
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if(root == null)return 0;
Deque<TreeNode>st = new LinkedList<>();
st.push(root);
int res = 0;
while(!st.isEmpty()){
int siz = st.size();
for(int i = 0;i < siz;i++){
TreeNode node = st.poll();
if(node.left != null){
st.push(node.left);
if(node.left.left == null && node.left.right == null)res += node.left.val;
}
if(node.right != null){
st.push(node.right);
}
}
}
return res;
}
}时间复杂度O(n)
空间复杂度O(n)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号