进制转换

二进制转十进制

• 二进制的每一位都遵循“逢二进一”的规律，每个位上允许出现的数字仅有 “0/1”，每遇到 2 就要进一位。
• 从个位向左，每一个位上的位权值依次为：\(2^0,2^1,2^2,\dots,2^i\)。位权值是指该位上一个数字“1”所代表的数值。
  例如：\(1001_2=1\times 2^0 + 1\times 2^3=9_{10},110_2=1\times 2^1+1\times 2^2=6_{10}\)

R进制转十进制

• R进制的每一位都遵循“逢R进一”的规律，每个位上允许出现的数字有 “\(0\sim R-1\)” 共 \(R\) 个，每遇到 \(R\) 就要进一位。
• 从个位向左，每一个位上的位权值依次为：\(R^0,R^1,R^2,\dots,R^i\)。
  例如：\(1001_R=1\times R^0 + 1\times R^3,110_2=1\times R^1+1\times R^2\)
  \(312_5=2\times 5^0 + 1\times 5^1 + 3\times 5^2=2+5+75=82_{10}\)

十进制转二进制

短除法口诀：除二倒取余，直到商为零，即不断拿当前的商去除以 2，得到的余数依次记下，直到商为 0 时，倒着将之前得到的余数自右向左写出。

十进制转R进制

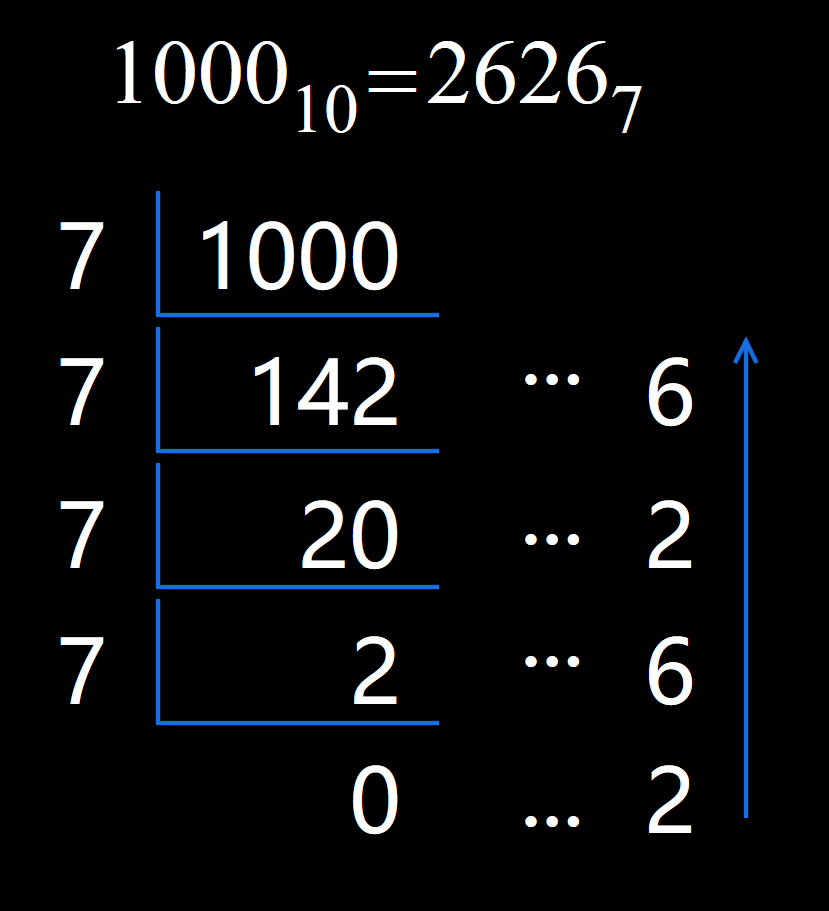
短除法口诀：除R倒取余，直到商为零，即不断拿当前的商去除以 R，得到的余数依次记下，直到商为 0 时，倒着将之前得到的余数自右向左写出。

二进制与八进制、十六进制之间的转换

1. 二进制和八进制
   由于八进制每个位上的数字可以为 “\(0\sim 7\)”，与三个二进制位表示的数字刚好相等(\(000_2=0_8,001_2=1_8,\dots,111_2=7_8\))。因此一个八进制位可以直接等价为三个二进制位。

• 二进制转成八进制
  将二进制从右向左，每 3 个位一组，转成对应的八进制数，若最后不够 3 个位，用 0 填充即可。
• 八进制转成二进制
  直接将每个位转为 3 个二进制位即可。
  例如：\(61_8=110001_2,1001101_2=115_8\)

2. 二进制和十六进制
   由于十六进制每个位上的数字可以为 “\(0\sim 15\)”，与四个二进制位表示的数字刚好相等(\(0000_2=0_{16},0001_2=1_{16},\dots,1111_2=15_{16}???\))，但是等等 \(15_{16}=1\times 16^1+5\times 16^0=21_{10}\)？？？。

仔细想想，原因应该是：\(15_{10}\) 应该只占十六进制的一个位！！！

而 \(10_{10}\sim 15_{10}\) 都是两位十进制数，我们没有对应用一个阿拉伯数字表示这几个数的方法！

所以，当一个进制数大于 10 时，我们无法仅用阿拉伯数字来表示这种进制一个位上的所有大于 9 的数字了。

解决方案是：我们借用 A~Z 的大写字母来做对应，\(A:10,B:11,C:12,D:13,E:14,F:15,\dots,Z:35\)，这样，十六进制上每个位的 16 个数字就可以写成：0~9,A~F，因此一个十六进制位可以直接等价为四个二进制位。

• 二进制转成十六进制
  将二进制从右向左，每 4 个位一组，转成对应的十六进制数，若最后不够 4 个位，用 0 填充即可。
• 十六进制转成二进制
  直接将每个位转为 4 个二进制位即可。

例如：\(6C_{16}=1101100_2,1001101_2=4D_{16}\)

3. 八进制与十六进制
   八进制与十六进制没有好的方法可以直接互相转换，通常需要先将它们转为二进制，再转为对应的八进制、十六进制。