数组
1、如何存储 n 个数
输入 n 个数,把这 n 个数按某种顺序输出。
#include <cstdio>
int main() {
//3 个数按序输出
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
printf("%d %d %d", a, b, c);
return 0;
}
当输入的数据量非常巨大时(比如:几百万),我们是无法挨个进行变量命名的。这个时候,我们需要给这一组数整体命名,然后具体每个数,给排一个编号即可。例如:当需要输入 100 位同学的语文成绩时,我们可以给这一组数起一个统一的名字,叫 score。具体的每位同学的成绩,根据班级序号进行排列即可,若小郁同学在班里的序号为 39,他的语文成绩为 98 分,则 score[39] = 98;
score[39] = 98;//score就叫做数组,score[39]代表小郁同学的语文分数
score[22] = 99;//score[22]代表小孟同学的语文分数
2、数组的声明
和变量一样,一个数组的所有元素都只能是一个相同的数据类型,比如,都为 int,或者都为 char。声明的时候,在名字后面要用一对中括号,里面填写这个数组要包含的数据个数。
int score[100];//声明一个语文分数的数组,共可以存储 100 个数据,编号为 0 ~ 99
注意:编号是从 0 开始的,最大编号比声明的数据个数要少 1。
类似的,我们还可以声明其他类型的数组
//声明了一个可以存储 55 个 double 类型数据的数组,编号为 0 ~ 54
double len[55];
//声明了一个可以存储 70 个 char 类型数据的数组,编号为 0 ~ 69
char ch[70];


多维数组在内存中存储时,根据不同的处理器架构,分为行优先存储与列优先存储两种方式:
- 相邻两个元素是同一行的,称为“行优先”;
- 相邻两个元素是同一列的,称为“列优先”。
我们日常使用的电脑,均为行优先存储。
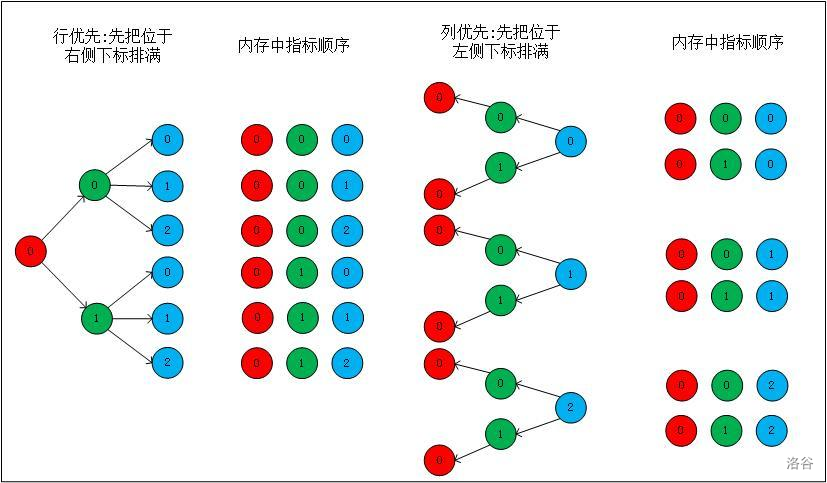
上图中,红色点为第一维,绿色点为第二维,蓝色点为第三维。
3、数组的输入、输出
数组由于数据量通常巨大,因此需要借助 for 循环来完成输入、输出,以及其他对数组中某些元素的处理任务。
#include <cstdio>
int main() {
//10 个数按序输出
int a[10];
//使用数组,我们可以借助循环变量 i,来对数组的第 i 个数进行输入、输出及其他操作
for (int i = 0; i < 10; ++i)
scanf("%d", &a[i]);
for (int i = 0; i < 10; ++i)
printf("%d ", a[i]);
return 0;
}
通常,题目中要求输入的数量都是万级为单位的,这时候,我们需要把数组声明到 main 函数的外面,作为“全局变量”。“全局变量”才可以声明 50 万 以上级别的数组,最大不要超过 2000万。
#include <cstdio>
//const int 是声明一个不能改变的常量 N,它在这个程序里永远都是 10 万
const int N = 1e5;
int a[N];
int main() {
//先输入一个正整数 n,接着连续输入 n 个数
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++i)
scanf("%d", &a[i]);
//将这 n 个数按输入顺序依次输出
for (int i = 0; i < n; ++i)
printf("%d ", a[i]);
return 0;
}
数组名
在定义数组之后,根据数组中元素的类型及个数,在内存中分配一段连续存储单元用于存放数组中的各个元素。
数组定义后,数组名表示该数组所分配连续内存空间中第一个单元的地址,即首地址。
数组定义后,数组名的值是一个地址,不可以被修改。

数组定义后,只能引用单个的数组元素,而不能一次引用整个数组,数组名单独出现的时候,仅仅代表首地址。
1e5 就是\(1\times {10^5}\)
与 int 型数组一样,不论数组类型是什么样的,下标始终是整型数。
#include <cstdio>
const int N = 1e3;
double a[N];
int main() {
//先输入一个正整数 n,接着连续输入 n 个数
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++i)
//scanf("%lf", a + i); a数组里的第 i 个元素的地址
scanf("%lf", &a[i]);
//将这 n 个数按输入顺序依次输出
for (int i = 0; i < n; ++i)
printf("%.3f ", a[i]);
return 0;
}
两个数组整体赋值函数
memset()函数:逐个字节地给数组赋值,需要
#include <cstring>fill()函数:逐个元素地给数组赋值,需要
#include <algorithm>
bool vis[107];// 每个元素占 1 个字节
char a[107];// 每个元素占 1 个字节
int b[107];// 每个元素占 4 个字节
double c[107];// 每个元素占 8 个字节
| 语句 | 作用 |
|---|---|
memset(vis, true, sizeof vis); |
给数组 vis 每个元素都赋值为 true |
memset(vis, true, 3); |
for (int i = 0; i < 3; ++i) vis[i] = true; |
memset(a, 'a', sizeof a); |
给数组 a 每个元素都赋值为 'a' |
memset(a, -1, sizeof a); |
给数组 a 的每个元素的每个字节赋值为 -1(-1的补码为 \(11111111_2\)) |
memset(b, 0, sizeof b); |
给数组 a 的每个元素的每个字节赋值为 0 |
memset(b, 0x7F, sizeof b); |
给数组 a 的每个元素赋值约为21亿,表示正无穷 INF,不可用于加法,会溢出 |
memset(b, 0x3F, sizeof b); |
给数组 a 的每个元素赋值约为10亿,也表示正无穷 INF,可用于加法,不会溢出 |
memset(b, 0x80, sizeof b); |
给数组 a 的每个元素赋值约为-21亿,表示负无穷 INF,不可用于加法,会溢出 |
memset(b, 0xC0, sizeof b); |
给数组 a 的每个元素赋值约为-10亿,也表示负无穷 INF,可用于加法,不会溢出 |
memset(c, 0x7F, sizeof c); |
给数组 a 的每个元素赋值约为\(10^{306}\),表示正无穷 INF,可用于加法,不会溢出 |
memset(c, 0xFE, sizeof c); |
给数组 a 的每个元素赋值约为\(-10^{303}\),表示负无穷 INF,可用于加法,不会溢出 |
fill(a, a+10, 4); |
for (int i = 0; i < 10; ++i) a[i] = 4; |
全局变量、static变量与局部变量

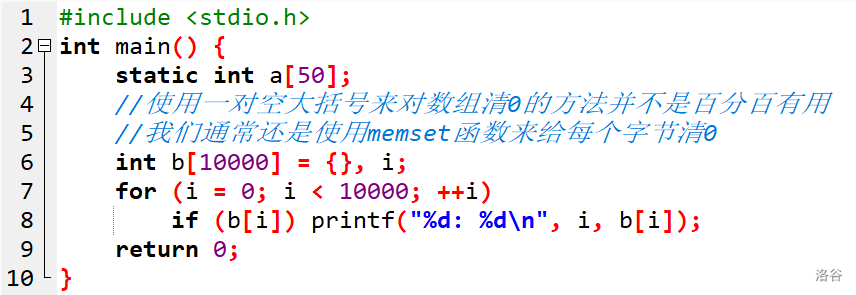

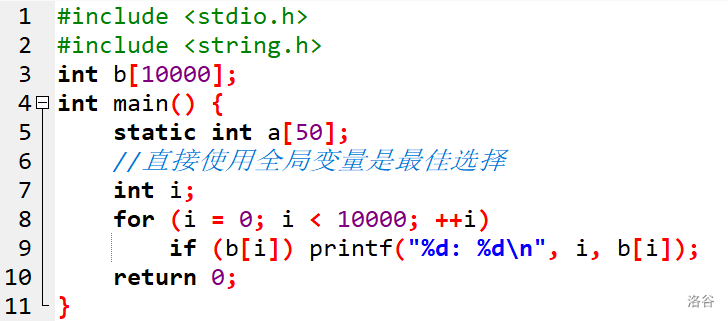
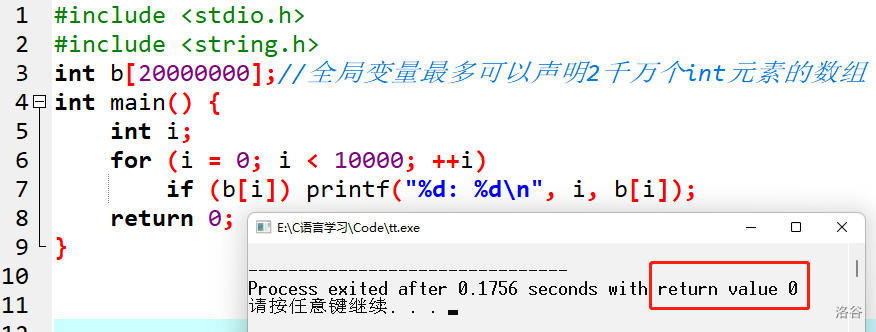
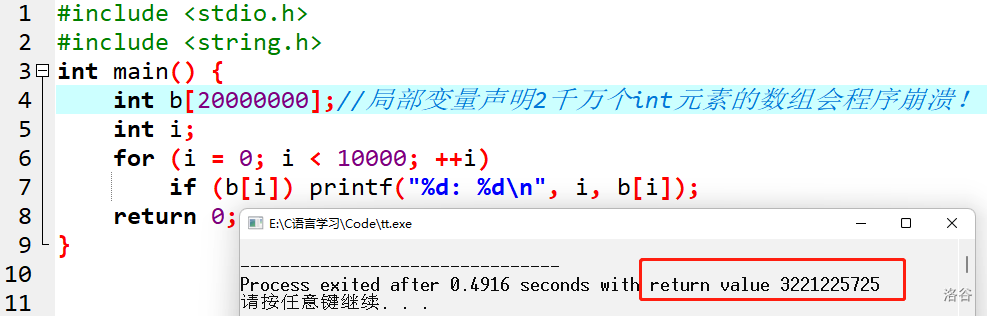
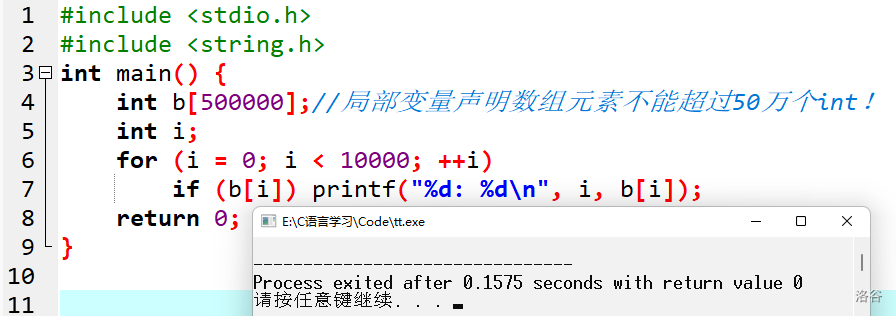
4、标记数组(桶)的应用
在有些题目中,我们需要对一些状态进行标记,我们称之为“标记数组”。
用数组中每个下标的位置当作一个桶标记,用来存储与下标号对应含义的数据。
-
应用1:
标记一个数是否出现,
v[2]=1表示标记 2 在数列中出现过,v[5]=0标记 5 没在数列之中; -
应用2:
标记一个数出现的次数,
v[2]=6表示 2 出现了 6 次。(常用) -
应用3:
标记一个数的前后关系,例如:
nx[i]表示i后面出现的数的下标。
注意:
- 作为下标的数字必须是非负整数!
- 下标是数列中的数字,而非它们的位置!
- 标记数组的大小取决于数列中的数值的取值范围,而不是数列中的数字个数!
点击查看代码
#include <stdio.h>
int a[10007];
int main () {
int L, M, ct = 0, s, t, i;
scanf("%d%d", &L, &M);
while (M--) {// 循环M次
scanf("%d%d", &s, &t);
// i从s变到t,每次加1
for (i = s; i <= t; ++i) {
a[i] = 1;//标记第i个位置的树被移走了
}
}
for (i = 0; i <= L; ++i) {
if (a[i] == 0) {// 如果第i个位置的树没被移走,ct加1
++ct;
}
}
printf("%d", ct);
return 0;
}
点击查看代码
#include <stdio.h>
#include <math.h>
int a[3007];
int main () {
int n, last, x, i, d;// diff
scanf("%d%d", &n, &last);
for (i = 2; i <= n; ++i) {
scanf("%d", &x);
d = abs(x - last);
if (!d || d>=n || a[d]) {
puts("Not jolly");
return 0;
}
a[d] = 1;
last = x;
}
puts("Jolly");
return 0;
}
点击查看代码
#include <stdio.h>
int a[10007];
int main () {
int n, i, x, mn = 10000, mx = 0;
scanf("%d", &n);
for (i = 1; i <= n; ++i) {
// 标记数组的输入方式
// 输入的数值作为下标使用
scanf("%d", &x);
if (mn > x) mn = x;
if (mx < x) mx = x;
a[x] = 1;
}
// 标记数组统计结果时,循环的方式不是1~n
// 而是整个数列的取值范围
for (i = mn; i <= mx; ++i) {
if (a[i]) {
// 标记数组的下标才是数列的值,而不是a[i]
printf("%d ", i);
}
}
return 0;
}
前缀和
已知给定的 n 个整数,求任意的第 x 个数到第 y 个数的和。
例如:
第一行输入两个整数 \(n\)(输入的数的个数:\(1\le n \le 10^6\)),\(m\)(询问次数,\(1\le m \le 10^6\))
第二行连续输入 \(n\) 个数(所有的数均在 \(int\) 范围内)
接下来 \(m\) 行,每行输入两个整数 \(x\) 和 \(y\),代表一次询问,第 x 个数到第 y 个数的和。
5 3
9 1 2 0 6
2 4
1 3
2 5
3
12
9
声明一个前缀和数组
s[N]在输入
a[i]的同时,计算前缀和s[i] = s[i-1] + a[i];求第
x个元素到第y个元素的区间和:s[y] - s[x-1];
#include <cstdio>
const int N = 1e6 + 7;
int a[N], n, m, x, y;
long long s[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
scanf("%d", a + i);
s[i] = s[i-1] + a[i];
}
for (int i = 1; i <= m; ++i) {
scanf("%d%d", &x, &y);
printf("%lld\n", s[y]-s[x-1]);
}
return 0;
}
记录的意义在于:可以去掉大量的重复工作,使速度得到巨大的提升!
记录本身不应该占用过大的工作量
6、差分
- 差分算法介绍
现有一个有 11 个元素的整型数组 d,所有元素都为 0。下面我们来看 2 步操作(从1号下标开始存储数据):
| d[0] | d[1] | d[2] | d[3] | d[4] | d[5] | d[6] | d[7] | d[8] | d[9] | d[10] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
(1)给 d[3] 加上 2
d[3] = 2;
(2)求 d 数组的前缀和
for (int i = 1; i <= 10; ++i)
d[i] += d[i-1];
这时候,d 数组变成了这样
| d[0] | d[1] | d[2] | d[3] | d[4] | d[5] | d[6] | d[7] | d[8] | d[9] | d[10] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
以上两个操作合到一起,实现了将数组中从第3个往后的所有元素均赋值为 2 的效果。
由上可见,一个全 0 的数组,只需要给起点的元素加上一个值,即如同“记录”下——对该起点到终点的所有元素统一加上这个值。不过真正的修改,需要通过求前缀和来实现。
注意:数组的初值为 0 非常重要!
那么,如何实现修改一个区间内(不再是到数组最后元素)的值呢?例如,将 d 数组的 [5, 8] 的元素都加上 3,怎么办?
这时候,我们实际上需要做两次刚才的操作:
(1)给 d[5] 加上 3
| d[0] | d[1] | d[2] | d[3] | d[4] | d[5] | d[6] | d[7] | d[8] | d[9] | d[10] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 |
(2)给 d[9] 加上 -3
| d[0] | d[1] | d[2] | d[3] | d[4] | d[5] | d[6] | d[7] | d[8] | d[9] | d[10] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | -3 | 0 |
(3)求 d 数组的前缀和(前缀和一定要在最后做)
| d[0] | d[1] | d[2] | d[3] | d[4] | d[5] | d[6] | d[7] | d[8] | d[9] | d[10] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 3 | 3 | 3 | 3 | 0 | 0 |
我们做 2 次记录:先将 5~最后 的所有元素都加上 3,再将 9~最后 的所有元素都加上 -3。这样,9~最后 的所有元素 +3 和 -3 就抵消了,相当于没变。最终,我们成功实现了将 [5, 8] 的元素全部加上 3。
如果我们把每个区间都挨个加一遍,那么最多需要 \(10^6\times 10^6=10^{12}\)次操作,就会 \(TLE\)。
那么,能否把所有的区间操作合并到一起,只执行一遍呢?当然可以
1. 将每个区间要做的操作快速地记录下来;
2. 统一对区间执行一次求前缀和操作。
以上就是刚才演示的 d 数组的 2 步操作。由于 d 数组要求初值必须为 0,所以,我们不能在原数组上直接进行操作,需要再单独声明一个 d 数组,求完前缀和之后,再将其与原数组对应位置相加即可。
#include <cstdio>
typedef long long LL;//注意取值范围,需要用long long
const int N = 1e6 + 7;
LL a[N], d[N];
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%lld", a+i);
for (int i = 1, x, y, z; i <= m; ++i) {
scanf("%d%d%d", &x, &y, &z);
d[x] += z, d[y+1] -= z;
}
for (int i = 1; i <= n; ++i) {
d[i] += d[i-1];
printf("%lld ", a[i] + d[i]);
}
return 0;
}
7.二维数组
二维数组通常被理解为数组的数组,例如:int a[5][3]; 可以看作是一个由 5 个一维数组(包含 3 个元素的数组)构成的另一个一维数组(包含 5 个元素的数组),其中,每个元素又是一个一维数组。
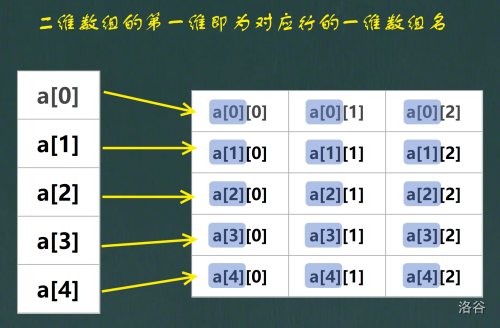

其中,所有的元素地址按从左到右,从上到下的顺序依次排列。
#include <iostream>
//内部的每个大括号代表对一行元素从左到右依次赋值
//如果元素数不够,后面的元素不赋值
int a[5][3] = {{1, 2}, {3, 4}, {5, 6, 7}, {8}, {9}};
int main() {
int *p = a[0];
for (int i = 0; i <= 14; ++i) printf("%d ", p[i]);
return 0;
}
//1 2 0 3 4 0 5 6 7 8 0 0 9 0 0
(1)int、double等数值类型的输入与输出
直接采用 2 层循环,外层对行循环,内层对列循环,枚举每个元素 [i][j] 进行赋值。
#include <iostream>
int a[5][3];
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]);//a[i]+j也可以
//输出需要注意换行和空格
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j)
printf("%d ", a[i][j]);
puts("");
}
return 0;
}
有时候,我们会使用如下的一个技巧:
我们都知道一对双引号内的内容会被看成一个字符串,也就是字符数组,只不过其中的内容是不可更改的。我们在输出的时候,可以利用这个特点。
#include <iostream>
int a[5][3];
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]);//a[i]+j也可以
//" \n"[0]代表空格," \n"[1]代表回车
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
printf("%d%c", a[i][j], " \n"[j==m]);
return 0;
}
(2)多行字符串输入
有时候,我们会遇到如下的输入:
输入的第一行包含一个整数 \(n(1\le n\le 1000)\) 和一个字符 \(c\),中间用一个空格隔开;
第二行起,连续输入 \(n\) 行只包含小写字符的长度在 50 以内的字符串。
3 y
abcd
efgh
ijkl
#include <iostream>
using std::cin;
const int N = 1007;
char a[N][57];
int main() {
int n;
char c;
cin >> n >> c;
for (int i = 1; i <= n; ++i) cin >> a[i];
//注意在输出的时候,"\n"比endl要快很多
for (int i = 1; i <= n; ++i) std::cout << a[i] << "\n";
return 0;
}
#include <iostream>
const int N = 1007;
char a[N][57];
int main() {
int n;
char c;
scanf("%d %c", &n, &c);
for (int i = 1; i <= n; ++i) scanf("%s", a[i]);
for (int i = 1; i <= n; ++i) printf("%s\n", a[i]);
return 0;
}
如果输入格式改成这样:
输入的第一行包含一个整数 \(n(1\le n\le 1000)\) 和一个字符 \(c\),中间用一个空格隔开;
第二行起,连续输入 \(n\) 行只包含小写字符和空格的长度为 \(n\) 的字符串。
5 y
ab cd
e fgh
ijk l
e fgh
ijk l
如果使用 scanf 进行读入,就容易出现问题:
#include <iostream>
const int N = 1007;
char a[N][N];
int main() {
int n;
char c;
scanf("%d %c", &n, &c);
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
scanf("%c", a[i] + j);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j)
printf("%c", a[i][j]);
puts("");
}
return 0;
}
/*
5 y
ab cd
e fgh
ijk l
e fgh
ab c
d
e f
gh
ij
k l
e
fgh
*/
造成上面结果的原因,正是循环里的 scanf("%c", a[i]+j);。它会把上一行的回车也作为输入存入二维数组之中,从而造成混乱的局面。
解决的方法:把字符作为字符数组输入。
#include <iostream>
const int N = 107;
char a[N][N];
int main() {
int n, i;
char c;
// %c 后面要把作为格式\n输入,方便下面scanf直接输入字符串
scanf("%d %c\n", &n, &c);
for (i = 0; i < n; ++i) {
scanf("%[^\n]", a[i]);
// 除了最后一行,每行后面都有一个换行符
if (i < n-1) getchar();
}
for (i = 0; i < n; ++i)
puts(a[i]);
}
#include <iostream>
using namespace std;
const int N = 1007;
char a[N][N];
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);//cin,cout加速
int n;
char c;
cin >> n >> c;
//多加一句cin.getline,将上一行的回车处理掉
cin.getline(a[0], N);
for (int i = 0; i < n; ++i)
cin.getline(a[i], N);
//注意在输出的时候,"\n"比endl要快很多
for (int i = 0; i < n; ++i)
cout << a[i] << "\n";
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号