字符串哈希

引例

题目描述

给定一个字符串 \(A\) 和一个字符串 \(B\)，求 \(B\) 在 \(A\) 中的出现次数。\(A\) 和 \(B\) 中的字符均为英语大写字母或小写字母。

\(A\) 中不同位置出现的 \(B\) 可重叠。

输入格式

输入共两行，分别是字符串 \(A\) 和字符串 \(B\)。

输出格式

输出一个整数，表示 \(B\) 在 \(A\) 中的出现次数。

样例输入

zyzyzyz
zyz

样例输出

3

数据范围与提示

\(1 \leq A, B\) 的长度 \(\leq 10 ^ 6\)，\(A\)、\(B\) 仅包含大小写字母。

暴力求解思路

逐一枚举 \(A\) 中的位置 \(i\) 作为 \(B\) 的起点，检查是否可以匹配，时间复杂度为 \(O(n^2)\)，显然会超时。

一、进制

通过对各种进制的观察，我们不难发现：

• 任意一个 \(R\) 进制的数，都可以看成是一个满足如下条件的字符串：
  • 每个位上都是 \([0, R-1]\) 之间的一个数字；
  • 两个字符串相等，当且仅当这两个字符串代表的 \(R\) 进制数相等。
• 判断两个字符串相等，需要一层循环，是 \(O(n)\) 的，而判断两个数相等，是 \(O(1)\) 的。
• 所有英文字母的取值范围都在 \(128\) 以内，因此，每个英文字母均可以看成是一个 \(R(R\ge 128)\) 进制数的基数值，任意一个字符串均可看作有一个或多个位的 \(R\) 进制数。

\[\begin{aligned} H("abcd") &= 97\cdot R^3+98\cdot R^2+99\cdot R+100 \\\\ H("ab") &= 97\cdot R+98 \\\\ H("cd") &= 99\cdot R+100=H(abcd)-H(ab)\cdot R^2 \end{aligned} \]

不难看出，在已知某个字符串的所有前缀的 \(R\) 进制数值的前提下，计算任意一个子串的 \(R\) 进制数值只需 \(O(1)\) 的时间（当然还需要预处理出 \(R^i\) 的值）。

至此，对于上面的题目，我们可以：

1. 把 \(B\) 转为一个 \(R\) 进制数 \(hb\)，时间复杂度为 \(O(n)\)。
2. 逐一枚举 \(A\) 中的位置 \(i\)，预处理出 \(A\) 的前 \(i\) 位构成的 \(R\) 进制数的数值 \(h[i]\)，时间复杂度为 \(O(n)\)。
3. 逐一枚举 \(A\) 中的位置 \(i\)，用 \(O(1)\) 的时间求出 \(A\) 中从第 \(i\) 个位开始的与 \(B\) 相同的一个字符串对应的 \(R\) 进制数 \(ha\)，检查是否满足 \(hb=ha\)。

按照这个思路，整个算法的时间复杂度就降到了 \(O(n)\)，可以通过了。

但是等等，这里好像有一个问题：由于 \(R\) 是大于等于 \(128\) 的数，\(R^i\) 很容易就会超出 \(int\) 甚至 \(long\ long\) 的取值范围，我们根本无法存储。而如果采用大整数来运算及存储，就得不偿失了。

那该怎么办呢？

我们遇到了一个取值范围远大于表示范围的对应问题，就如同关键字与位置下标的对应问题，要将取值范围非常大的一组数（字符串的 \(R\) 进制数值），尽量没有冲突地均匀存入一个空间有限的数组（基础变量类型的取值范围）中，这是标准的散列问题。

二、散列

设计这种散列函数一定要简单且快，通常采用经典的“除留余数法”，为了减少冲突，我们需要做 \(2\) 件事情：

• 要让余数的取值范围尽量大（采用最大的数据类型 unsigned long long，相当于模 \(2^{64}\)）。
• \(R\) 选取一个大于 \(128\) 的素数，例如：\(131,13331\) 等等。

\[\begin{aligned} H("abcd") &= 97\times 131^3+98\times 131^2+99\times 131+100\\\\ &=218064827+1681778+12969+100\\\\ &=219746605 \end{aligned} \]

那么，上面为什么没有去模 \(2^{64}\) 呢？因为 unsigned long long 本身恰好就是 \(64\) 位，它计算出来的结果本来就是只保留小于 \(2^{64}\) 的部分，这称作自然溢出。

好啦！到此为止，我们就完成了真个算法设计，看看代码吧！

#include <iostream>
#include <cstring>
using namespace std;
using ULL = unsigned long long;
const int N = 1e6 + 7, P = 131;
ULL sum[N], sa, pw[N];
char s[N];
int main() {
	scanf("%s", s + 1);
	pw[0] = 1;
	int len = strlen(s + 1);
	for (int i = 1; s[i]; ++i) {
		sum[i] = sum[i-1] * P + s[i];
		pw[i] = pw[i-1] * P;
	}
	scanf("%s", s + 1);
	int lena = strlen(s + 1), ans = 0;
	for (int i = 1; s[i]; ++i)
		sa = sa * P + s[i];
	for (int i = 1; i+lena-1 <= len; ++i) {
		ULL d = sum[i+lena-1] - sum[i-1]*pw[lena];
		if (d == sa) 
			++ans;
	}
	printf("%d", ans);
	return 0;
}

三、遗留问题

我们都知道散列一定会出现冲突的，理论上一定存在两个不同字符串的散列值相同，对策有两条：

• 仅用散列判断两个字符串不同，即若两个字符串的散列值不同，那它们一定是两个不同的字符串。
• 当两个字符串的散列值相同时，可以采用以下两种策略之一：
  • 双哈希，即再用另一个素数计算以下散列，看看是否相同。
  • 直接判断，即用循环比对一下字符串是否相同。

四、Border

字符串S中，既是S的前缀又是S的后缀的子串，称为S的Border。

一个字符串可以有多个Border，比如 aabaaba 的Border可以有：a, aaba, aabaaba（本身）。

特别的，S是自己的平凡Border，S的其余Border都称为它的非平凡Border。

这是字符串中的一个非常重要的概念，下面是关于Border的一些性质：

1. Border不具有二分性，不能通过二分的方法求最长的非平凡Border。

2. Border的传递性：Border的Border也是字符串的Border，求一个字符串所有的Border就是求字符串所有前缀的Border。

3. \(p\) 是S的周期等价于 \(|S|-p\) 是S的Border。

4. 对于回文串S的后缀 \(t\)，它是S的Border当且仅当它是回文串。

5. \(t\) 是字符串S的Border(\(S\le 2|t|\))，S是回文串当且仅当 \(t\) 是回文串。

证明：

S是回文，\(t\)当然也是回文。

\(t\) 是回文时，\(i\le \lfloor {s\over 2}\rfloor\) 时，

\[S[i]=S[|t|+1-i]=S[|t|+1-i+|S|-|t|]=S[|S|+1-i] \]

得证。

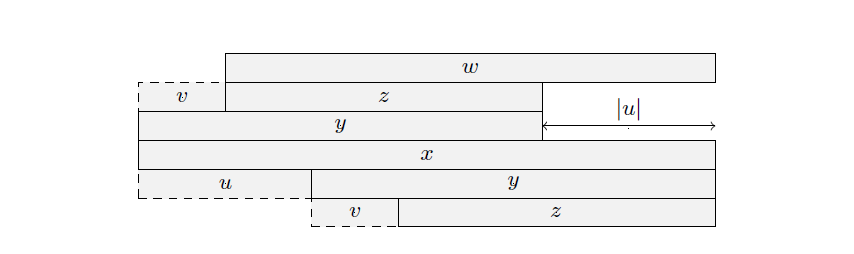
6. \(x\) 是一个回文串，\(y\) 是 \(x\) 的最长回文真后缀，\(z\) 是 \(y\) 的最长回文真后缀，令 \(u,v\) 分别为满足 \(x=uy,y=vz\) 的字符串，则有下面三条性质：

（1）\(|u|\ge |v|\)

（2）如果 \(|u|\gt|v|\)，那么 \(|u|\ge|z|\)

（3）如果 \(|u|=|v|\)，那么 \(u=v\)

证明：

（1）\(|u|=|x|-|y|\) 是\(x\)的最小周期，\(|v|=|y|-|z|\) 是 \(y\) 的最小周期。考虑反证法，假设\(|u|\lt|v|\)，因为 \(y\) 是 \(x\) 的后缀，所以 \(u\) 既是 \(x\) 的周期，也是 \(y\) 的周期，而 \(|v|\) 是 \(|y|\) 的最小周期，矛盾。所以 \(|u|\ge |v|\)。

（2）因为 \(y\) 是 \(x\) 的Border，所以 \(v\) 是 \(x\) 的前缀，设字符串 \(w\) 满足 \(x=vw\)，其中 \(z\) 是 \(w\) 的Border。考虑反证法，假设 \(|u|\le |z|\)，那么 \(|zu|\le 2|z|\)，所以由性质5，\(|w|\) 是回文串，由性质4，\(w\) 是 \(x\) 的Border，又因为 \(|u|\gt|v|\)，所以 \(|w|\gt|y|\)，矛盾。所以 \(|u|\gt|z|\)。

（3）\(u,v\) 都是 \(x\) 的前缀，\(|u|=|v|\)，所以 \(u=v\)。

7. S的所有回文后缀按照长度排序后，可以划分为 \(log|S|\) 段等差数列。

证明：

设 S 的所有回文后缀长度从小到大排序为 \(l_1,l_2,\dots,l_k\)。对于任意 \(2≤i≤k−1\)，若 \(l_i−l_{i−1}=l_{i+1}−l_i\)，则 \(l_{i−1},l_i,l_{i+1}\) 构成一个等差数列。否则 \(l_i−l_{i−1}≠l_{i+1}−l_i\)，由性质7，有 \(l_{i+1}−l_i>l_i−l_{i−1}\)，且 \(l_{i+1}−l_i>l_{i−1}\)，\(l_{i+1}>2l_{i−1}\)。因此，若相邻两对回文后缀的长度之差发生变化，那么这个最大长度一定会相对于最小长度翻一倍。显然，长度翻倍最多只会发生 \(O(log|S|)\) 次，也就是 S 的回文后缀长度可以划分成 \(log|s|\) 段等差数列。

该推论也可以通过使用弱周期引理，对 S 的最长回文后缀的所有 Border 按照长度 \(x\) 分类，\(x∈[2^0,2^1),[2^1,2^2),…,[2^k,n)\)，考虑这 \(log|S|\) 组内每组的最长 Border 进行证明。详细证明可以参考金策的《字符串算法选讲》和陈孙立的 2019 年 IOI 国家候选队论文《子串周期查询问题的相关算法及其应用》。

8. 非空回文字符串S如果存在一个回文后缀T，那么S的形式必然可以表示为YXYXY...XY的形式。这里X,Y为回文串，可以为空串。并且 \(|X|+|Y|=|S|-|T|,|Y|=|S|\mod |S|-|T|\)。

五、拓展问题

在字符串匹配问题中，经常需要求一个串在另一个串中的匹配次数，例如下面的题目：

题目描述

给定若干个长度 \(\le 10^6\) 的由可见字符构成的字符串，询问每个字符串最多是由多少个相同的子字符串重复连接而成的。如：ababab 则最多由 \(3\) 个 ab 连接而成。

输入格式

输入若干行，每行有一个字符串。

特别的，字符串可能为 . 即一个半角句号，此时输入结束。

样例输入

abcd
aaaa
ababab
.

样例输出

1
4
3

数据范围与提示

字符串长度 \(\le 10^6\)。

枚举思路

直接枚举前缀子串的长度（长度显然是总长度的一个因子），检查是否能够重复覆盖整个字符串，时间复杂度为 \(O(n^2)\)。

有没有一种办法，可以直接判断出一个前缀 \(a\) 是否可以通过重复连接构成原字符串 \(b\) 呢？

仔细观察下图，长为 12 的字符串，abcdefghiABCDEFGHI 都是 char 类型变量，各自代表对应位置的一个字符。

如果其前 \(9\) 个字符构成的前缀与最后 \(9\) 个字符构成的后缀能够匹配，即 abcdefghi=ABCDEFGHI，是否就说明整个字符串可以用前 \(3\) 个字符重复连接构成？

1	2	3	4	5	6	7	8	9	10	11	12
*	*	*	a	b	c	d	e	f	g	h	i
A	B	C	D	E	F	G	H	I	*	*	*

证明：
首先，对应位置的字符分别相等，即 abc=DEF
又由 abcdef=ABCDEF，可知 abc=ABC，
由此可得 abc=ABC=DEF=def，
同理，由 def=GHI, GHI=ghi 可得 abc=def=ghi，得证。

参考博文：

1. 最小回文划分

2. Border原理