前缀和与差分

前缀和

令 \(s[i]\) 为 \(a\) 数组前 \(i\) 个元素之和，称为 \(a\) 数组的前缀和。

求前缀和数组

利用 \(s[i]=s[i-1] + a[i]\) 的性质，使用一层循环更新每个位置的前缀和。

for (int i = 1; i <= n; ++i) {
    scanf("%d", a + i);
    s[i] = s[i-1] + a[i];
}

如果 \(a\) 数组的单个元素后续不再使用，我们可以仅使用 \(s\) 数组，录入 \(a[i]\) 时直接改为录入 \(s[i]\)

for (int i = 1; i <= n; ++i) {
    scanf("%d", s + i);
    s[i] += s[i-1];
}

前缀和的应用

1. 求区间和，例如 \(a_5+a_6+a_7+\dots +a_{11}\)，本来需要一层 \(for\) 循环累加求和，现在可以使用 \(s[11]-s[4]\) 直接计算得出，对于一般的 \(a_i+a_{i+1}+a_{i+2}+\dots+a_j\) 的和，可以使用以下公式：

   \[\sum_{k=i}^j a[k]=s[j]-s[i-1] \]

2. 给一个位置及后续的所有位置同时加上一个变量，例如将第 \(5\) 个数往后的所有位置均加上 \(3\)。

   首先，我们需要一个初始化为 0 的数组 \(d\)

   分两步：

   1. 在 \(d\) 数组的起始位置加上一个数 \(x\)，​
   2. 对 \(d\) 数组求前缀和。

   例如：\(n=10\) 的数组 \(d\)（下标从 \(0\) 开始），要将第 \(5\) 个数往后的所有位置均加上 \(3\)。

   第 \(1\) 步：\(d[5] += 3\)，数组变为：\([0,0,0,0,0,3,0,0,0,0]\)

   第 \(2\) 步：直接在数组 \(d\) 上求前缀和数组 \(s\)：\([0,0,0,0,0,3,3,3,3,3]\)

   当我们需要对多个起始位置执行操作时，只需先执行所有的第 \(1\) 步，然后统一执行一次第 \(2\) 步即可。

   例如，\(n=10\) 的数组 \(d\)（下标从 \(0\) 开始），要将第 \(5\) 个数往后的所有位置均加上 \(3\)，将第 \(3\) 个数往后的所有位置均减去 \(2\)。

   第 \(1\) 步：\(d[5] += 3\)，数组变为：\([0,0,0,0,0,3,0,0,0,0]\)​

   ​ \(d[3]+=-2\)，数组变为：\([0,0,0,-2,0,3,0,0,0,0]\)

   第 \(2\) 步：直接在数组 \(d\) 上求前缀和数组 \(s\)：\([0,0,0,-2,-2,1,1,1,1,1]\)​

   这样，我们仅需两个一层 \(for\) 循环即可完成，而普通方法需要用两层 \(for\) 循环才能完成。原因在于，我们成功地将操作分解成了两部分，而其中需要单独操作的第一部分仅需要一个赋值语句，更新所有数据的部分可以统一只做一次。

差分

对一个数组的某个区间 \([i,j]\) 的每个数均加上 \(z\)。

根据前缀和的第 \(2\) 个应用，我们可以将这个区间更新的问题转化为两次前缀和的应用：

1. 将 \([i,n]\) 的每个数均加上 \(z\)；
2. 将 \([j+1, n]\) 的每个数均加上 \(-z\)。

请看以下模板题：

#include <iostream>
using namespace std;
const int N = 1e6 + 7;
using LL = long long;
LL d[N], a[N];
int main() {
	int n, m;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++i) 
		scanf("%lld", a + i);
	while (m--) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		d[x] += z, d[y+1] -= z;
	}
	for (int i = 1; i <= n; ++i) {
		d[i] += d[i-1];
		printf("%lld ", a[i] + d[i]);
	}
}

二维前缀和与差分

1、二维前缀和 && 区间和

#include <cstdio>
const int N = 1007;
int sum[N][N];
int main() {
    int n, m, q;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j) {
            scanf("%d", &sum[i][j]);

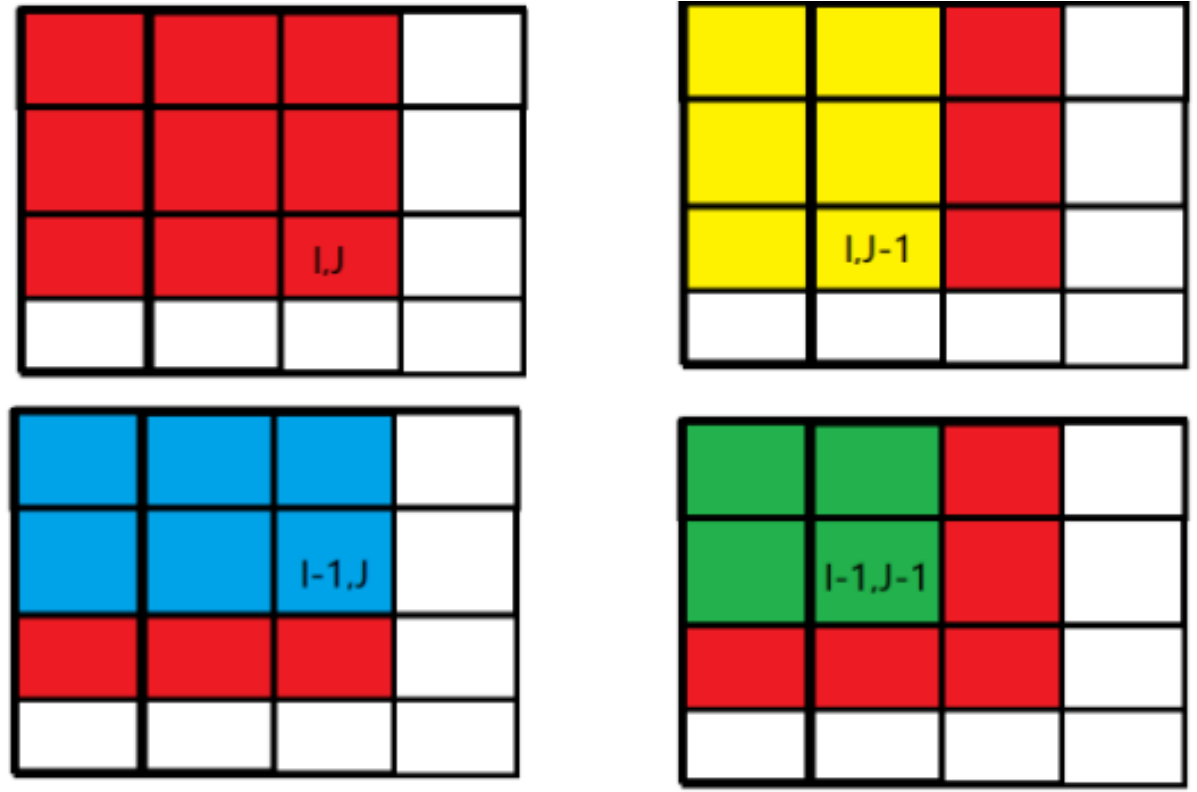
			sum[i][j] += sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1];
        }
	scanf("%d", &q);
	while (q--) {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);

		int ans = sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1-1][y1-1];
		printf("%d\n", ans);
    }
	return 0;
}

2、二维差分

一位数组差分：将 [i, j] 内的所有元素加 a，只需标记 d[i] += a, d[j+1] -= a

#include <cstdio>
const int N = 1007;
int n, m, d[N][N], sum[N][N];
void preSum(int a[][N]) {
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			a[i][j] += a[i-1][j] + a[i][j-1] - a[i-1][j-1];
}
int getSum(int a[][N], int x1, int y1, int x2, int y2) {
	return a[x2][y2] - a[x2][y1-1] - a[x1-1][y2] + a[x1-1][y1-1];
}
int main() {
    int q, x, x1, y1, x2, y2;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            scanf("%d", &sum[i][j]);
   	scanf("%d", &q);
    while (q--) {
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &x);

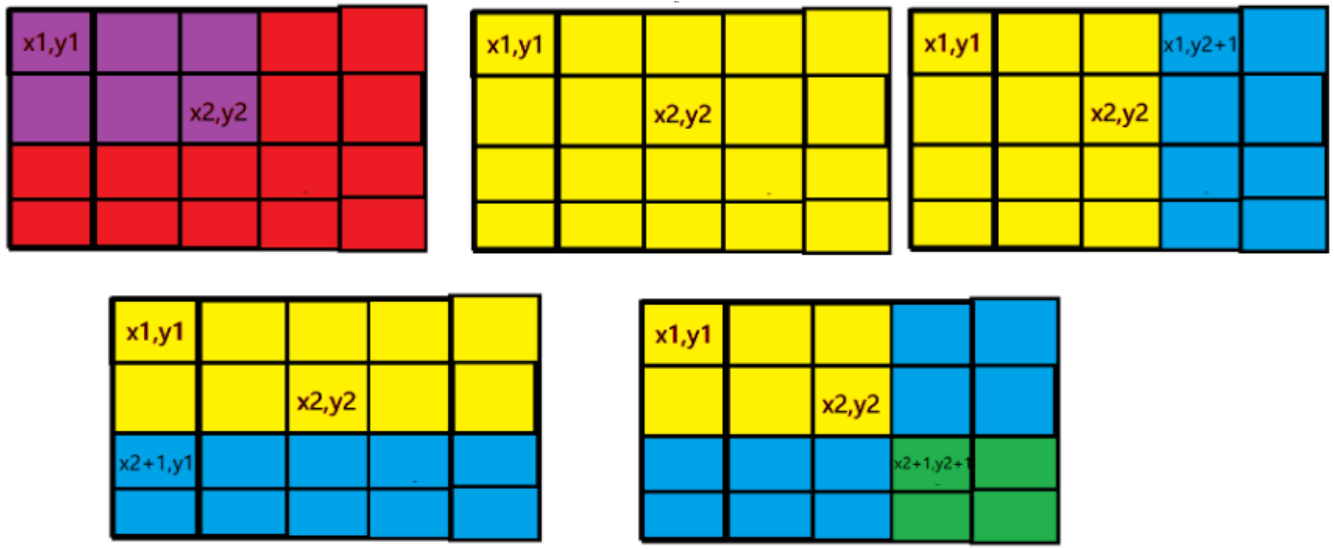
		d[x1][y1] += x, d[x1][y2+1] -= x, d[x2+1][y1] -= x, d[x2+1][y2+1] += x;
    }
    preSum(d), preSum(sum), preSum(d);
   	scanf("%d", &q);
    while (q--) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        int ans = getSum(sum, x1, y1, x2, y2) + getSum(d, x1, y1, x2, y2);
		printf("%d\n", ans);
    }
    return 0;
}
/*
5 7
1 2 3 4 5 6 7
7 6 5 4 3 2 1
2 3 4 5 6 7 1
3 4 5 6 7 1 2
4 5 6 7 1 2 3
2
2 4 3 5 -2
4 3 5 5 1
3
2 3 3 5
3 4 4 6
5 5 5 5
*/