kmp 字符串匹配算法

一、引例

题目描述

原题来自：HDU 2087

一块花布条，里面有些图案，另有一块直接可用的小饰条，里面也有一些图案。对于给定的花布条和小饰条，计算一下能从花布条中尽可能剪出几块小饰条来呢？

输入格式

输入数据为多组数据，读取到 # 字符时结束。每组数据仅有一行，为由空格分开的花布条和小饰条。花布条和小饰条都是用可见 ASCII 字符表示的，不会超过 \(1000\) 个字符。

注意：这个 # 应为单个字符。若某字符串开头有 #，不意味着读入结束！

输出格式

对于每组数据，输出一行一个整数，表示能从花纹布中剪出的最多小饰条个数。

样例

abcde a3
aaaaaa aa
#

0
3

数据范围与提示

对于全部数据，字符串长度 \(\leq 1000\)。

思路1

首先考虑采用哈希。

思路2——KMP算法

考虑一种更快、代码量更少的方法——KMP算法。

我们令第一个字符串为 s，第二个字符串为 t，需要求出 t 在 s 中不重叠的匹配个数。

KMP算法的思想：在匹配 s 的过程中，每次遇到失配的点 s[i]!=t[j]，我们应该快速地选择 t[0...j-1] 的 border（参见字符串哈希），实现不往回移动 i 的前提下，快速地完成 s[0...i-1] 的后缀与 t 串前缀的最长匹配，由于外层下标 i 从左至右只走一遍，每次匹配时，j 同 i 一起向前移动，撤回border的次数一定小于向前移动的次数，因此整体时间复杂度为 \(O(n)\)。

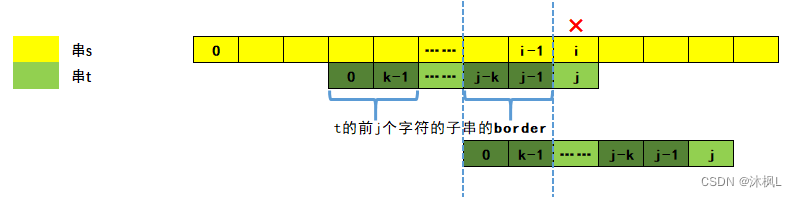
因此，问题转换为如何求出串 t 所有前缀的最大非平凡border，即实现一个前缀函数。

前缀函数

定义 nx[i] 表示 t[0...i] 的最长非平凡border的长度，特别地，nx[0] 为 0。

从 t[1] 开始逐个求前缀函数 t[i] 的过程如下：

1. 设border长度的初值 int j = 0;
2. while (j && t[i]!=t[j]) j = nx[j-1];// t[i] 失配时，从长到短依次尝试 t[i-1] 的每一个border
3. if (t[i] == t[j]) ++j;// 若找到了某个border，可以匹配 t[i]，匹配长度加 1。
4. nx[i] = j;// 记录 t[i] border的长度

void match() {
	for (int i = 1, j = 0; t[i]; ++i) {
		while (j && t[i]!=t[j]) j = nx[j-1];
		if (t[i] == t[j]) ++j;
		nx[i] = j;
	}
}

Z算法（扩展KMP）

Z算法（Z-Algorithm）是一种字符串算法，在国内也常常被叫做拓展KMP算法。

我们知道，KMP算法的核心就是那张部分匹配表，其实它也被称为前缀函数，记作 \(\pi\)。对一个字符串而言，我们定义既是它前缀又是它后缀的字符串是它的border，那 \(\pi(i)\) 就表示 \(s[0\dots i]\) 的最长border的长度。或者说， \(\pi(i)\) 是满足 \(s[0\dots x-1]=s[i-x+1\dots i]\) 的最大的 \(x\) （特别地，令 \(\pi(0)=0\) ）。

而Z算法的核心是Z函数，它的定义与 \(\pi\) 非常相似。 \(Z(i)\) 定义为 \(s\) 与 \(s[i\dots n-1]\) 的最长公共前缀（LCP）。或者说，\(Z(i)\) 是满足 \(s[0\dots x-1]=s[i,i+1,\dots, i+x-1]\) 的最大的 \(x\) （特别地，令 \(Z(0)=0\)）。

例如，设有字符串aabcaabcaaaab，那么它的Z函数值如下表所示：

现在我们来探究如何快速求出这张表。

设 \(Z(i)\neq 0\)，那么我们定义区间 \([i,i+Z[i]-1]\) 为一个Z-Box，显然，Z-Box对应的子串一定也是整个字符串的一个前缀。例如，上表中 \([4,9]\) 就是一个Z-Box，它对应的子串是aabcaa，也是整个字符串的一个前缀。

这里直接放上精美的代码：

void getZ(char s[]) {
    int l = 0;
    for (int i = 1; s[i]; ++i) {
        if (l+z[l] > i) 
            z[i] = min(z[i-l], l + z[l] - i);
        while (s[i+z[i]] && s[z[i]]==s[i+z[i]]) 
            ++z[i];
        if (i+z[i] > l+z[l]) 
            l = i;
    }
}

以上代码利用了如下性质：

对于 \(i\gt 0\)，对任意 \(0\le l\lt i\) 都可以递推得到：

\[\forall 0\le x\lt min(z[i-l], l+z[l]-i),\text{均有 } s[i+x]=s[0+x] \text{ 成立。} \]

证明：

\[\begin{aligned} &s[i+x]\\ =&s[l+(i+x-l)]\\ =&s[0+(i+x-l)](\text{需满足 }x\le l+z[l]-i\text{，即 }i+x-l\le z[l])\\ =&s[(i-l)+x]\\ =&s[0+x](\text{需满足}x\le z[i-l]) \end{aligned} \]

所以可以选定某个 \(0\le l\lt i\)，初始化 \(z[i]=min(z[i-l], l+z[l]-i)\)，然后暴力判断字符相等增加 \(z[i]\)。

这里 \(l\) 选满足 \(j+z[j](0\le j\lt i)\) 最大的 \(j\)，这样每个字符只会被暴力判断一次，所以时间复杂度可以做到 \(Θ(n)\)。

习题：

1. 【模板】扩展KMP/exKMP(Z函数)

应用

知道了Z函数的求法后，我们来看它的几个简单应用：

给出字符串 \(a, b\)，求 \(a\) 的每个后缀与 \(b\) 的LCP。

设 $ 为字符集外字符，求 \(b+\\\)+a$ 的Z函数，则 \(a\) 的后缀 \(a[i\dots]\) 与 \(b\) 的LCP为 \(Z[|b|+1+i]\) 。

给出文本串 \(s\) 和模式串 \(p\) ，求 \(p\) 在 \(s\) 中的所有出现位置。

这是KMP和字符串哈希的经典题目，但也可以用Z算法。设 \(\\\)$ 为字符集外字符，求 \(p+\\\)+s$ 的Z函数，则每一个 \(Z[i]=|p|\) 都对应 \(p\) 在 \(s\) 中的一次出现。

求 \(s\) 的所有border。

虽然这个是KMP裸题，但也可以用Z算法。求 \(s\) 的Z函数。对于每一个 \(i\)，如果 \(i+Z[i]=|s|\)，说明这个Z-Box对应一个border。（注：与KMP不同，这里只是求所有border，不是求所有前缀的border）

求 \(s\) 的每个前缀的出现次数。

求 \(s\) 的Z函数。对于每一个 \(i\)，如果 \(Z[i]\) 不等于0，说明长度为 \(Z[i],Z[i]-1,\dots,1\) 的前缀在此处各出现了一次，所以求一个后缀和即可。在这个问题中一般令 \(Z[0]=|s|\)。

for (int i = n + 1; i < 2 * n + 1; ++i)
    S[z[i]]++;
for (int i = n; i >= 1; --i)
    S[i] += S[i + 1];