初学者常见数学问题

获取一个十进制数的个位

可选择的数学运算符有：%（求余数）。

int a;
cin >> a;// 输入 376
cout << a%10;// 输出 6

任何一个十进制整数模 10 （除以10 的余数）的结果，就是其个位上的数字。

获取一个十进制的某个位上的数字

int a; cin >> a;// 输入一个十进制数

• 十位：a%100/10 或 a/10%10

  例如：\(a=376\)，\(376\%100/10=76/10=7\)​ ，\(376/10\%10=37\%10=7\)

• 百位：a%1000/100 或 a/100%10

• 千位：a%10000/1000 或 a/1000%10

• \(\dots\)

给定个位、十位、百位的数字，拼出这个三位数

已知一个三位数的个位是 \(6\)，十位是 \(7\)，百位是 \(3\)，这个三位数是 \(3\times 100 + 7\times 10 + 6=376\)

已知一个三位数的个位是 \(a\)，十位是 \(b\)，百位是 \(c\)，这个三位数是 c*100 + b*10 + a

这样得到的三位数，与 \(\overline{cba}\) 有区别吗？有！若 \(c\) 是 \(0\)，\(b\) 是 \(7\)，\(a\) 是 \(6\)，\(\overline{cba}=076\)，而通过上面的运算得到的是 \(76\)，没有前导 \(0\)。

计算 \(a^b\)

需要 #include <cmath> 头文件，使用 \(pow\) 函数。

power n. 幂，乘方（数学名词）

\(pow(a, b)\) 求 \(a\) 的 \(b\) 次方，即 \(a^b\)，返回结果为 \(double\) 类型。

#include <iostream>
#include <cmath>
using namespace std;
int main() {
	double a, b;
	cin >> a >> b;
	cout << pow(a, b);//求 a 的 b 次方
	return 0;
}

等差数列求和公式（需记忆）

\((首项+末项)\times 项数\div 2\)

例如：\(2+5+8+11+14=(2+14)\times 5\div 2=40\)

简单推导步骤：

依次从两端各取一个数配对，它们的和都相等：\(2+14=16,5+11=16\)，和除以 \(2\) 正好是中间数（即平均数），乘以项数，就相当于 \(8+8+8+8+8=40\)

等比数列求和公式

\[a+a\ast q+a\ast q^2+a\ast q^3+\dots+a\ast q^n=a{q^{n+1}-1\over q-1} \]

例如：

\[3+3\times 2+3\times 2^2+3\times 2^3=3\times{2^4-1\over 2-1}=3\times 15=45 \]

求和公式

例1.

\[sum = \sum_{i=1}^n a_i \]

以上公式为 \(a_1+a_2+\dots +a_n\) 的和，即

int sum = 0;
for (int i = 1; i <= n; ++i)
    sum += a[i];

例2.

\[sum=\sum_{k=1}^m a_{i,k} \]

为 \(a_{i,1}+a_{i,2}+\dots+a_{i,m}\) 的和，为嵌入在 \(i\) 循环中的一段求和：

for (int k = 1; k <= m; ++k)
    sum += a[i][k];

输出三个数的排序结果

1、枚举所有排列情况

将 \(3\) 个变量的 \(6\) 种排列依次枚举，进行判断，输入对应的结果。

2、通过交换进行排序

（1）先确定最小的数，然后确定次小数
例如：\(3,1,2\)，先通过 \(3\) 和 \(1\) 比较，将较小的放在最前面，变成 \(1,3,2\)，再将 \(1\) 和 \(2\) 比较，确定 \(1\) 是最小的；接着将 \(3\) 和 \(2\) 比较，确定次小的是 \(2\)，与 \(3\) 交换，变成 \(1,2,3\)。
（2）先确定最大的数，再确定次大数
做法同上。

在 C\C++ 中，% 符号为求模运算符，即 a%b 表示 a 除以 b 的余数。

周期问题

我们在奥数中经常遇到这样的问题：

1. 给你一串数字 4 5 6 4 5 6 4 5 6 ...，求这里的第 1000 个数字是几？

我们发现这是一个周期数列，周期为 3。

a. 如果将4看作第 1 个数，第 1000 个数一定是周期中的第 1 个数 4，因为前面 999 个数刚好是 333 组 456 构成的循环。

b. 如果将4看作第 0 个数，那么第 1000 个数此时就对应为第 999 个数，因为 999 模 3 余数为 0，同样对应的是 4。

2. 给你一串数字 0 1 2 3 4 5 6 4 5 6 4 5 6...，求这里的第 1000 个数字是几？

这还是一个周期数列，周期为 3，但是它是从第 5 个数开始循环的，因此我们应该用 (1000-4) % 3，算出来是 0，这该怎么办呢？

针对这个问题，我们可以有两种处理方法：

（1）特殊处理：遇到 0 时，取周期中的最后一个数 6；

（2）统一处理：我们不要从 1 开始数，由于 % 运算会出现 0，因此我们就从 0 开始数。我们将第一个循环的数字 4 （目前是第 5 个数）变成第 0 个数，重新写算式 (1000-5) % 3，结果为 2，则 456 中，4 作为周期的第 0 个数，那么 6 就是第 2 个数。

练习题：
凯撒密码

这一题里，每个字母都被变成它后面的第 3 个字母，因此直接将其 ASCII 码值加 3 即可。

但是，最后 3 个字母却遇到了问题，\(x\rightarrow a, y\rightarrow b, z\rightarrow c\)，这个不是加 3 能够实现的。如何解决呢？

我们可以想象一下，把 26 个字母看成上面那样的循环：\(a, b, c, d, \dots, z, a, b, c, d, \dots\)，这样的话，当我们遇到 \(x\rightarrow a\) 的问题时，\(x\) 是第 23 个字母（从 0 开始数的），就相当于求第 26 个字母（计算23+3得到）是什么。那很容易想到，第 26 个字母就是 \(a\)。

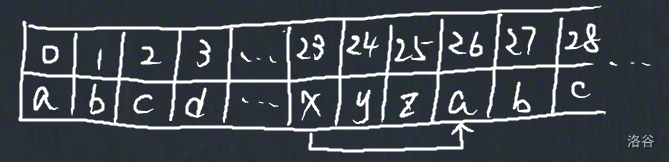
那么现在还有一个问题，就是在 C\C++ 中，'a' 是用 ASCII 值 97 存储的，其余字母的 ASCII 值依次是 \(98,99,\dots\)，我们需要先将 'a' 看成第 0 个字母，因此，如果我们要对一个字母变量 alpha 进行凯撒加密，计算其后面第 3 个字母时，需要先执行 alpha-'a'，然后再加 3，除以 26 取模，完整的算式应该是 (alpha - 'a' + 3) % 26 + 'a'。

#include <iostream>
using namespace std;
int main() {
    char alpha;
    cin >> alpha;
    //这里 'a' 就是97，尽量不要写 97，而是直接用 'a' 表示，这样可读性更强。
    alpha = (alpha - 'a' + 3) % 26 + 'a';
    cout << alpha;
    return 0;
}

求模运算的公式

\[\begin{aligned} &(1). (a+b+c)\%M=(a\%M+b\%M+C\%M)\%M \\ &(2).(a-b-c)\%M=((a\%M-b\%M-C\%M)\%M+M)\%M \\ &(3).(a*b*c)\%M=a\%M*b\%M*C\%M \\ &3^{60}\%7=(3^2\%7)^{30}\%7=2^{30}\%7=(2^3\%7)^{10}\%7=1^{10}\%7=1 \end{aligned} \]

快速幂（二进制拆分）

#include <iostream>
typedef long long LL;
LL qpow(LL a, int b, int M) {
    LL ans = 1;
    while (b) {
        if (b & 1) ans = ans * a % M;
        a = a * a % M, b >>= 1;
    }
    return ans;
}
int main() {
    int a, b, c;
    scanf("%d%d%d", &a, &b, &c);
    printf("%lld", qpow(a, b, c));
    return 0;
}