点分治【产品说明书】

淀粉质，淀粉质！

---

---

1|0产品用途

本章讲述本产品的用途，即大规模处理树上路径。

例：给出一棵n个点的树，求树上有多少条长度为k的路径？

何谓大规模？事实上，当$n$的大小达到$10^4$，就已经不小了。
本产品可以解决的问题范围大约为$n\leq 10^6$
（注：笔者是口胡的）

$\mathbf{Q.}$本产品vs朴素算法
$\mathbf{A.}$Of Course本产品！

本产品

拥有美丽的时间复杂度（$O(n\log^2n)$，部分可桶排优化至$O(\log n)$）

朴素算法1

枚举不同的点对，dfs求距离，拥有可爱的时间复杂度$O(n^3)$

朴素算法2

枚举不同的点对，lca求距离，拥有可爱的时间复杂度$O(n^2\log n)$

朴素算法3

呃，不太清楚，但听说暴力能拥有可爱的时间复杂度$O(n^2)$

---

---

2|0使用方法

本章讲述本产品的作用原理和实现方法。

2|1原理简介

顾名思义，淀粉质点分治就是按照树上的节点进行分治。得益于树美丽的结构，我们可以轻松地分而治之。

一棵树，可以在一次分治下被切割如下几个部分：根节点，子树，子树，……，子树。

当然，也可能没有子树，或者子树是一个节点……
这些对分治没什么影响的小小问题，甚至称不上特殊情况呢

2|2实现方法

分治点

那么每次分治的“根节点”应当如何选择呢？
可以画个图，但是笔者太懒，于是就口头解释

可以先暴力地考虑随便选一个点，然后思考可能存在的bug。
举一个极端情况：树是一条链。
由于随便选一个点，如果每次都选到链首作为根节点，那么总共需要分治$n$次。
（大寄的时间复杂度，甚至不如直接暴力）

所以随便选点肯定是哒咩的，选点的方法应该要符合某种规律。
这时候就该想想“树的杂七杂八东西”

树的杂七杂八东西，指：直径，中心，重心

发现重心是个好东西。
其实分治次数，与最大子树大小关联很强。
_{（主要是没自己证明，所以说法比较模糊，总之是这样的）}
重心恰巧是这方面的专业户，它的最大子树大小不会超过$n/2$。（可以利用反证法轻松得证）于是我们把 当前要分治的这棵树的重心 作为根节点进行分治，这样就可以保证复杂度不爆炸了。
_{（关于怎么求重心，考虑到篇幅还是不提了awa）}

统计答案

主要问题在于合并。
显而易见的，分治的两块都分别有部分答案。

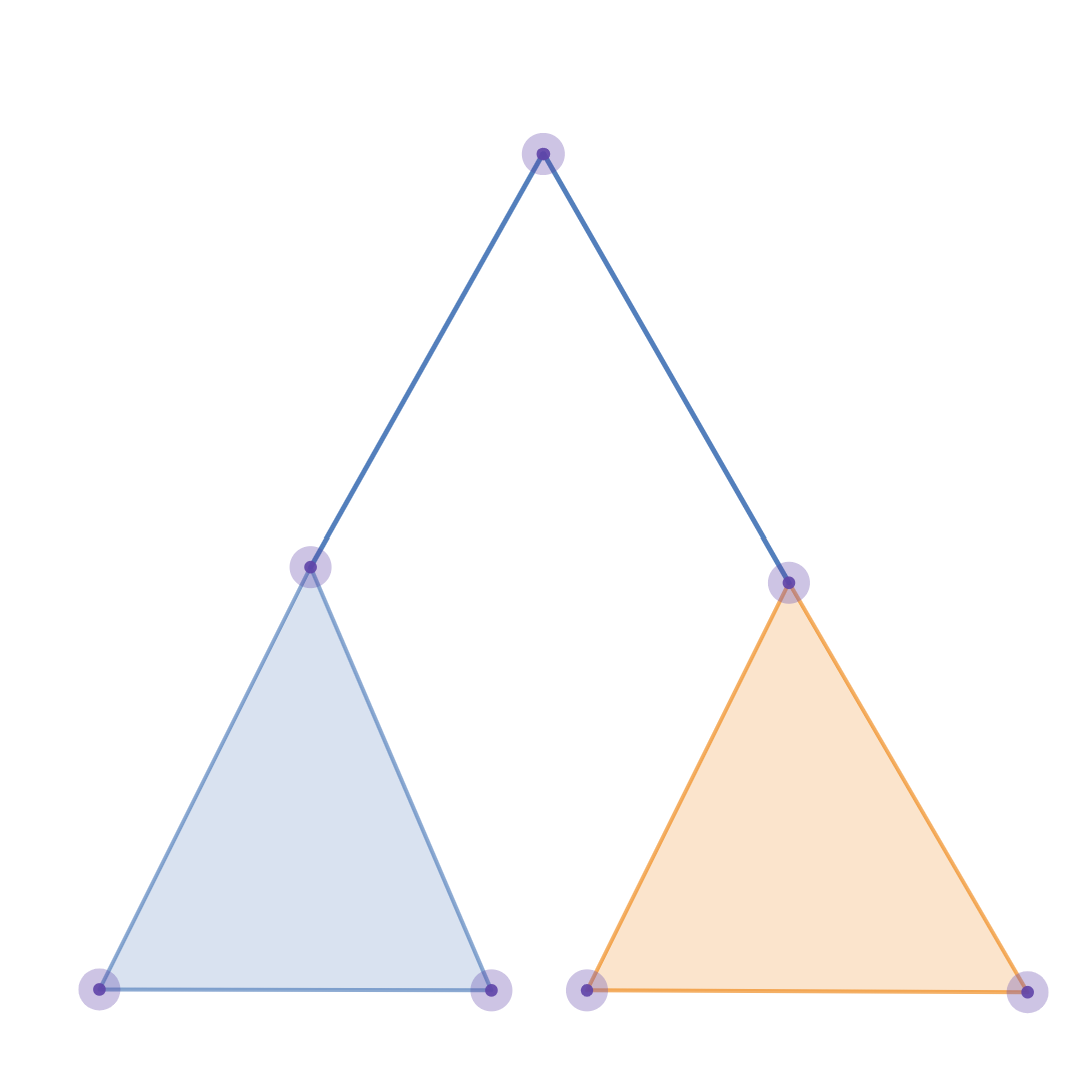
如图，我们已知蓝块和橙块分别包含多少k路径。合并时可以将这部分答案直接加入统计。而需要额外统计的答案是跨越两块的k路径。也就是一端在蓝色一端在橙色的路径。
如何统计这类路径呢？
暴力枚举两端点的时间复杂度是$O(n^2)$。非常的美丽呢！
虽然但是，枚举端点是无法避免的，我们可以选择只枚举一个端点。

Stop learning useless algorithms, go and solve some problems, learn how to use binary search!

考虑用二分来找另一个端点。可以给距离排序，然后二分出k路径的左右界位置。

在统计的时候还应当注意判重。
在一个子树中的节点到重心的路径会有一部分重合（也就是lca到root的那段路径）。这种情况下的k路径不能计入答案。特判解决这个问题。

---

---

完结撒花！

__EOF__

本文作者：Meteor2008
本文链接：https://www.cnblogs.com/meteor2008/p/17587767.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！