完全背包

完全背包

完全背包和01背包最大的区别就是01背包中，每个物品只有一个，完全背包中，每个物品有无穷个

思路

和01背包的状态转移方程也很像

01背包：

\[\left( i,v\right) =\begin{cases}\left( i-1,v\right) \\ \left( i-1,v-v_{i}\right) +w_{i}\end{cases} \]

完全背包：

\[\left( i,v\right) =\begin{cases}\left( i-1,v\right) \\ \left( i,v-v_{i}\right) +w_{i}\end{cases} \]

可以看到，它们只有一处不一样，因为完全背包每个物品有无限个。01背包中，如果准备要装i物品，那么i物品现在一定不在背包中；而在完全背包中，如果准备要装i物品，那么i物品现在也可能在背包中。

恰好装满

恰好装满的情况和正常情况只有初始值不一样，正常情况下，所有的初始值都是0，在恰好装满的情况下，初始值应该这样设置

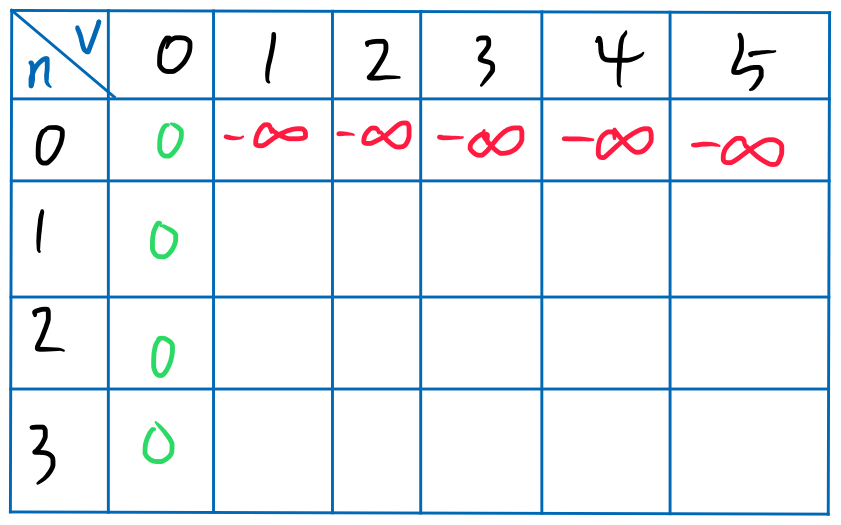
可以看到，当背包大小为0的时候，初始值都为0，因为对于容积为0的背包，一定是恰好装满，因为本来也啥也装不下。当有0件物品的时候，容积不为0的背包，初始值都设置为负无穷大，因为这些情况下，背包无法恰好装满。设置为负无穷大的原因为，便于在dp的过程中，将无法恰好装满的信息传递下去，因为负无穷大加任何数都是负无穷大

代码

二维dp

class Solution:
    def knapsack(self, v: int, n: int, nums: List[List[int]]) -> List[int]:
        nums = [[0, 0]] + nums
        dp1 = [[0] * (v + 1) for i in range(n + 1)]
        dp2 = [[0] * (v + 1) for i in range(n + 1)]

        for i in range(1, v + 1):
            dp2[0][i] = -float("inf")

        for i in range(1, n + 1):
            for j in range(1, v + 1):
                if nums[i][0] > j:
                    dp1[i][j] = dp1[i - 1][j]
                    dp2[i][j] = dp2[i - 1][j]
                else:
                    dp1[i][j] = max(dp1[i - 1][j], dp1[i][j - nums[i][0]] + nums[i][1])
                    dp2[i][j] = max(dp2[i - 1][j], dp2[i][j - nums[i][0]] + nums[i][1])


        return [dp1[n][v], dp2[n][v] if dp2[n][v] != -float("inf") else 0]

一维dp

class Solution:
    def knapsack(self, v: int, n: int, nums: List[List[int]]) -> List[int]:
        nums = [[0, 0]] + nums
        dp1 = [0] * (v + 1)
        dp2 = [0] + [-float('inf')] * v

        for i in range(1, n + 1):
            for j in range(1, v + 1):
                if nums[i][0] <= j:
                    dp1[j] = max(dp1[j], dp1[j - nums[i][0]] + nums[i][1])
                    dp2[j] = max(dp2[j], dp2[j - nums[i][0]] + nums[i][1])


        return [dp1[v], dp2[v] if dp2[v] != -float("inf") else 0]