推销员问题

　　旅行商问题，即TSP问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

　　这是我大二期末数据结构课程设计的题目之一，其是关于图这种数据结构的。按照其题目大意可以大致理解为一个旅行商，要从自己原本的城市出发，走遍所有的城市最后回到自己原来的城市。在这个问题中的约束是每个城市都只能拜访一次。目的是求旅行商走一圈得到的最短路径的大小。

　　对于这个问题，普遍有两种思路。第一种思路是暴力破解法。

　　举个例子。

　　

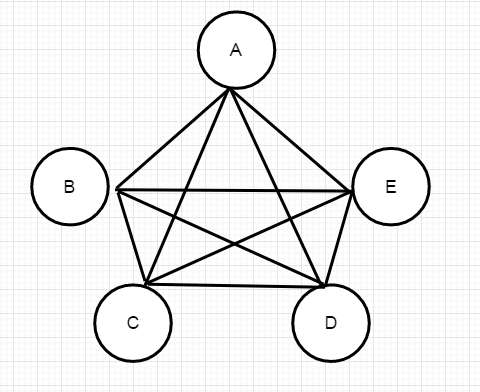
　　如图所示，一共有五个城市其彼此之间相互连通。旅行商要走完一圈回来且不重复，实际上走得路径的各种可能性也不过是各种城市的排列组合。

ABCDEA、ACBDEA、......等等，按照排列组合来计算共有4!种情况，在这些组合中选取一种距离最短的方式就好了。当城市数为5的时候看起来还好，但是这种暴力排列组合的时间复杂度是很大的，达到了O(n!)，所以对于城市数多的情况下，是很难算出结果的。

　　第二种，就是贪心法。所谓贪心法，就是每一步都走最短的路径，且通往的城市是没有访问过的。这种方法，可以得到尽可能短的路径，但是也会出现一种问题，就是局部最优解不一定是整体最优解，你可能一味的贪心得到是这样的结果，之前走的路都是最短的，但是最后返回原来城市的路径究极长，显然就不满足最短路径了。我的方法就属于这种贪心法，废话不多说了，上代码。

# include <stdio.h>
# include <string.h>
# include <stdlib.h>
# include <iostream>
# define INF 100000
# define max 100
using namespace std;
//推销员问题
typedef struct Graph{
    int distance[max][max];//城市与城市之间的距离 
    char place[max];
    int city;//城市的个数 
    int edge;//边的个数 
}CI,*PCI;//城市 
bool visited[max];//判断有没有访问过该城市
int order[max];//访问节点的顺序 
int  num_vertax(void);//求已经收入顶点集合的顶点的个数 
void init_graph(CI* G);//初始化城市 
void find_bestway(CI*G);//找到最好的路径
int locate_graph(CI*G,char elem);//找到顶点的下标位置
void show_graph(CI* G);//把图打印出来 
int main(void)
{
    char elem;
    PCI G=(PCI)malloc(sizeof(CI));
    
    init_graph(G);
    show_graph(G);
    find_bestway(G);
    free(G); 
    system("pause");
    return 0;
 } 
 void init_graph(CI* G)
 {
     int i,j;
     printf("请输入一共有多少个城市：\n");
     scanf("%d",&(G->city));
     ///初始化城市 
     for(i=0;i<G->city;i++)
     {
         for(j=0;j<G->city;j++)
         {
             if(i==j)
             {
                 G->distance[i][j]=0;
             }
             else
             {
                 G->distance[i][j]=INF;
             }
         }
     }
     printf("请输入城市的名称：\n");
     for(i=0;i<G->city;i++)
     {
         cin>>G->place[i];
     }
     ///输入城市与城市之间的距离
     for(i=0;i<G->city;i++)
     {
         for(j=0;j<G->city;j++)
         {
             if(G->distance[j][i]!=0&&G->distance[j][i]!=INF)
             {
                 G->distance[i][j]=G->distance[j][i];
             }
            else if(i!=j) 
             {
                 
                 printf("请输入%c城市与%c城市之间的距离：\n",G->place[i],G->place[j]);
                 scanf("%d",&G->distance[i][j]);
             }
         }
      } 
      
 }
 void find_bestway(CI* G)
 {///找到最好的路径并输出出来 
     char begin;//开始的城市
     int start;//开始城市的下标
    int end;//结束城市的下标 
    int remain;//记录下标 
    int count=1;//计数器
    int cost=0;//花费
    int next;
    int min_cost=0;//总的最小花费 
    for(int i=0;i<G->city;i++)//初始化所有城市都没有访问过 
    {
        visited[i]=false;
    }
    for(int i=0;i<max;i++)//顺序序号数组我们用-1初始化 
    {
        order[i]=-1;
    }
     cout<<"请输入您想从哪个城市出发"<<endl;
    cin>>begin;
    start=locate_graph(G,begin);
    cout<<"start="<<start<<endl;
    //开始的那一座城市声明已经访问过了
    remain=start;
    cout<<"remain="<<remain<<endl;
    visited[start]=true;
    order[0]=start;//访问顺序的第一个位置装着该下标
    while(num_vertax()<G->city)
    {
    //    cout<<"有"<<num_vertax()<<"个顶点已经加入"<<endl; 
        cost=INF;//初始化最大长度
        for(int i=0;i<G->city;i++)//在与它相邻的所有节点中
        {
             if(start!=i&&visited[i]==false&&G->distance[start][i]<cost)
             {
             //    cout<<"start="<<start<<endl;
             //    cout<<"i="<<i<<endl;
             //    cout<<"distance="<<G->distance[start][i]<<endl;
                 cost=G->distance[start][i];
             //    cout<<"第"<<"i="<<i<<"时候"<<cost<<endl; 
                 next=i;
                 
             }            
        } 
        //cout<<"start="<<start<<" ";
        start=next;
         visited[start]=true;//下一个开始的节点为访问过了
         order[count]=start;
         cout<<"cost="<<cost<<endl;
         min_cost=min_cost+cost;
         count++; 
    }
    
    //cout<<"之前min_cost="<<min_cost<<endl;
    order[count]=order[0];
    //cout<<"最后一段路为："<<G->distance[count-1][remain]; 
    //cout<<"remain="<<remain<<endl;
    //cout<<"最后节点下标为"<<order[count]<<endl;
//    cout<<"count="<<count; 
    //cout<<"last="<<G->distance[count][remain];
    min_cost=min_cost+G->distance[order[count-1]][remain];
    cout<<"最佳访问顺序为："<<endl;
    for(int i=0;i<G->city+1;i++)
    {
        cout<<G->place[order[i]]<<" ";
    }
    cout<<endl;
    cout<<"最短的距离为:"<<endl;
    cout<<min_cost;
     cout<<endl;
       
    
    
      
     
 } 
int locate_graph(CI* G,char elem)//返回节点所在的下标 
{
    int i;
    for( i=0;i<G->city;i++)
    {
        if(elem==G->place[i])
        {
          return i;
        }
    }
    
    
} 
int  num_vertax(void)//可以知道顶点集合之中一共有多少个顶点 
{ 
    
    int count=0;
    while(order[count]!=-1)
    {
        count++;
    }
    return count;
}
void show_graph(CI* G)//将图的内容打印出来
{
    int i,j;
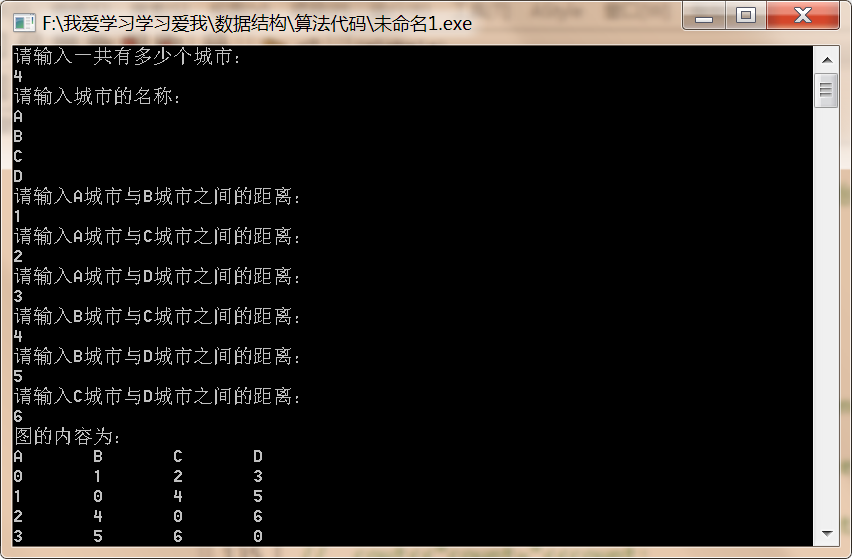
    printf("图的内容为：\n");
    for(i=0;i<G->city;i++)
    {
        printf("%c\t",G->place[i]);
     }
    printf("\n");
    for(i=0;i<G->city;i++)
    {
        for(j=0;j<G->city;j++)
        {
            printf("%d\t",G->distance[i][j]);
        }
        printf("\n");
     } 
}