力扣算法-42.接雨水-

侵删

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例 1：

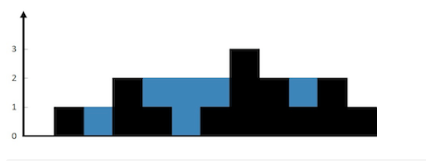
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
0 <= n <= 3 * 104
0 <= height[i] <= 105

思路一、暴力破解
从题目中可以看出，每个格子能否储存水以及存水量的大小，取决于它左右最高的格子和它的本身格子的大小，以第三个格子为例，左边的格子最大为1，右边的格子最大为
3，自身为0，所以该格子的存水量为min(左格子1,右格子3) - 自身0 = 1；并且第一个格子和最后一个格子不在计算之内，因为它们两边都没有边界，没办法存水。
所以，可以遍历每一个格子，然后计算它左右最大格子的大小并且与自身做对比。
复杂度：时间复杂度O(N^2)、空间复杂度O(1)
代码：

public int trap(int[] height)
{
      int len = height.length;
      //判断长度
      if(len < 3)
      {
            return 0;
      }
      int res = 0;//结果
      for(int i = 1;i < len-1;i++) //从第二个格子开始，到倒数第二个格子结束
      {
           int leftMax = leftMax(i,height);//计算左边最大格子
           int rightMax = rightMax(i,height,len);//计算右边最大格子
            
            //与自身做对比
            if(height[i] < min(leftMax,rightMax)){
                  res += min(leftMax,rightMax) - hieght[i];
            }
      }
      return res;
}
 private static int leftMax(int center, int[] height) { //计算左边最大格子
        int res = 0;
        for(int i = center - 1;i >= 0;i--)
        {
            res = Math.max(res,height[i]);
        }
        return res;
    }

    private static int rightMax(int center, int[] height, int len) {      //计算右边最大格子
        int res = 0;
        for(int i = center + 1;i < len;i++)
        {
            res = Math.max(res,height[i]);
        }
        return res;
    }

思路二、因为思路一空间复杂度为O(1),所以可以用空间换时间；
设置两个和原始数组等长的数组，分别用来记录原数组左右两边的最大格子
复杂度：时间复杂度：O(N),空间复杂度：O(N)
代码：

   public static int trap2(int[] height)
    {
        int len = height.length;
        if(len < 3)
        {
            return 0;
        }
        int[] left = new int[len];
        for(int i = 1;i < len - 1;i++)
        {
            left[i] = Math.max(left[i-1],height[i-1]);
        }
        int[] right = new int[len];
        for(int i = len - 2;i >= 0;i--)
        {
            right[i] = Math.max(right[i+1],height[i+1]);
        }
        int res = 0;
        for(int i = 1;i < len-1;i++)
        {
            if(height[i] < Math.min(left[i],right[i]))
            {
                res += Math.min(left[i],right[i]) - height[i];
            }
        }
        return res;
    }

思路三、双指针
复杂度：时间复杂度：O(N),空间复杂度：O(1)

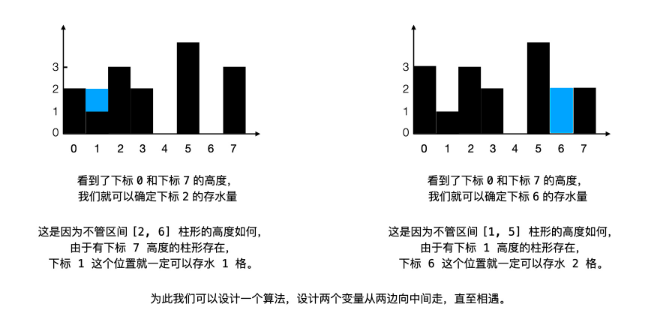
左边为minvalleftMax； 右边为minvalrightMax

代码：

public static int trap3(int[] height) //双指针
    {
        int len = height.length;
        if(len < 3)
        {
            return 0;
        }
        int leftMax = height[0];
        int rightMax = height[len - 1];

        int left = 1;//左指针
        int right = len - 2;//右指针

        int res = 0;
        while(left <= right)
        {
            int minVal = Math.min(leftMax,rightMax);
            if(minVal == leftMax)
            {
                if(minVal > height[left])
                {
                    res += minVal - height[left];
                }
                leftMax = Math.max(height[left],leftMax );
                left++;
            }else{
                if(minVal > height[right])
                {
                    res += minVal - height[right];
                }
                rightMax = Math.max(height[right],rightMax );
                right -- ;
            }
        }
        return  res;
    }