算法入门打卡Day4

今日收获

交换链表中的节点
快慢指针法删除链表倒数第N个节点
链表相交问题
环形链表问题
了解到了 && 运算符的特性

学习时长：3.5h

正文

两两交换链表中的节点

LeetCode24

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

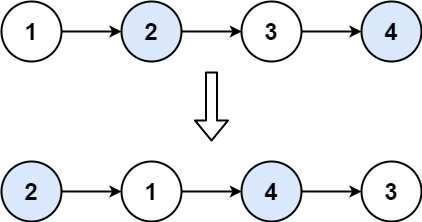
解答方法：画图找出增删方式，搞清链表的顺序，别搞错cur的位置就行。

class Solution {
public:
    ListNode* dummyHead = new ListNode;
    
    ListNode* swapPairs(ListNode* head) {
        dummyHead->next = head;
        ListNode* cur = dummyHead;
        ListNode* tmp1;
        ListNode* tmp2;
        while (cur->next != nullptr && cur->next->next != nullptr) {
            tmp2 = cur->next->next->next;
            tmp1 = cur->next->next;
            cur->next->next = tmp2;
            tmp1->next = cur->next;
            cur->next = tmp1;
            cur = cur->next->next;
        }
        return dummyHead->next;
    }
};

注意事项

每次为链表创建一个新节点时（比如虚拟头节点），一定要 new 一个新的堆区空间，因为这和 temp 临时指针不同，指针只是临时保存，而新节点是完全独立的有自己的值的。
如果不需要虚拟头节点了也请记得释放内存空间，把 dummyHead delete 掉。

删除链表的倒数第N个结点(快慢指针)

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

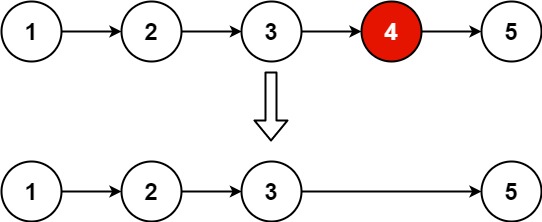
这里我们使用快慢指针法：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* dummyHead = new ListNode;
    
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        dummyHead->next = head;
        ListNode* slow = dummyHead;
        ListNode* fast = dummyHead;
        while (n + 1) {
            fast = fast->next;
            n--;
        }
        while (fast != nullptr) {
            slow = slow->next;
            fast = fast->next;
        }
        ListNode* tmp = slow->next;
        slow->next = tmp->next;
        delete tmp;
        return dummyHead->next;
    }
};

总体还是比较简单的：

快指针先移动 n 次，然后两个指针一起移动到快指针 fast 变空，这样慢指针 slow 会停留在需要被删除的元素上。
但是一般来说我们删除链表节点时停留在目标前一个节点来操作比较简单，所以这里我们让 fast 指针先移动 n+1 次就可以了。
记得释放被删除节点的内存空间防止内存泄漏。

链表相交

LeetCode面试题02.07

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

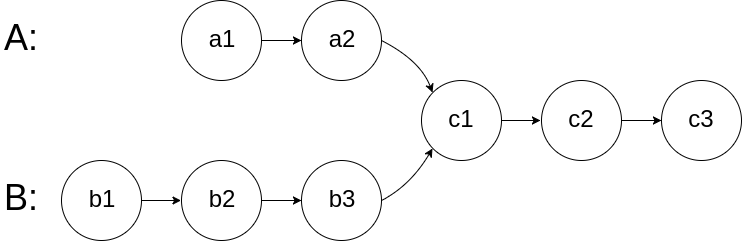
图示两个链表在节点 c1 开始相交：

题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int sizeA = 0, sizeB = 0;
        while (curA != nullptr) {
            curA = curA->next;
            sizeA++;
        }
        while (curB != nullptr) {
            curB = curB->next;
            sizeB++;
        }
        curA = headA;
        curB = headB;
        if (sizeA <= sizeB) {
            int c = sizeB - sizeA;
            while (c--) {
                curB = curB->next;
            }
        }
        if (sizeA > sizeB) {
            int c = sizeA - sizeB;
            while (c--) {
                curA = curA->next;
            }
        }
        while (curA != nullptr) {
            if (curA == curB) {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        return NULL;
    }
};

遍历两次求两链表长度差
对齐两个 cur 指针
一起向后遍历，遇到相同的指针返回值，没遇到返回 NULL

环形链表

LeetCode142

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

环形列表示例图：

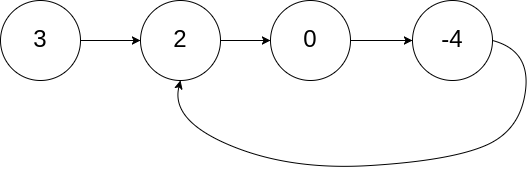
思路：

假设从头结点到环形入口节点的节点数为x。环形入口节点到 fast指针与slow指针相遇节点节点数为y。从相遇节点再到环形入口节点节点数为 z。如图所示：

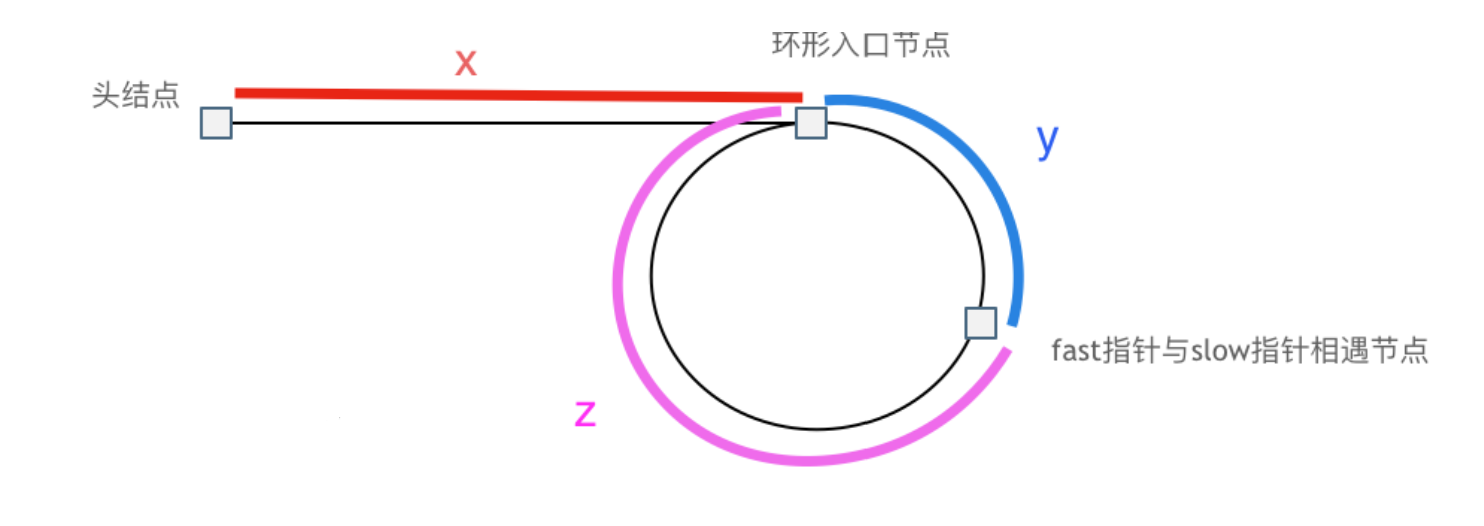
那么相遇时：

slow指针走过的节点数为: x + y，

fast指针走过的节点数：x + y + n (y + z)，

n为fast指针在环内走了n圈才遇到slow指针，（y+z）为一圈内节点的个数A。

fast指针走过的节点数 = slow指针走过的节点数 * 2：(x + y) * 2 = x + y + n (y + z)

因为要找环形的入口，那么要求的是x，因为x表示头结点到环形入口节点的的距离。所以要求x ，将x单独放在左面：x = n (y + z) - y

再从n(y+z)中提出一个（y+z）来，整理公式之后为如下公式：x = (n - 1) (y + z) + z ，

这是为了得到一个正数方便我们后面遍历，注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。

slow指针与fast指针相遇时，slow指针肯定是没有走完一圈的，因为fast指针的速度是slow的两倍，slow走一圈fast已经走两圈了。

这就意味着，从头结点出发一个指针，从相遇节点也出发一个指针，这两个指针每次只走一个节点，那么当这两个指针相遇的时候就是环形入口的节点。

也就是在相遇节点处，定义一个指针index1，在头结点处定一个指针index2。

让index1和index2同时移动，每次移动一个节点，那么他们相遇的地方就是环形入口的节点。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
            if (slow == fast) {
                ListNode* index1 = head;
                ListNode* index2 = slow;
                while (index1 != index2) {
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index1;
            }
        }
        return NULL;
    }
};

这里有一个隐蔽的知识点，在以下语句中： fast != nullptr && fast->next != nullptr ，哪怕 fast 是空指针，也不需要考虑调用 fast->next 会不会变成非法访问，因为运算符 && 是从左到右进行的，一旦左边的条件不能满足，就不会对右边的条件进行判断了，于是在类似的场景下注意不要写反！！

posted on 2026-02-01 15:49 Megumin777 阅读(0) 评论(0) 收藏举报

刷新页面返回顶部