短时傅立叶变换解析

博客中的文章均为 meelo 原创，请务必以链接形式注明本文地址

 

通过傅立叶变换可以得到信号的频谱。信号的频谱的应用非常广泛，信号的压缩、降噪都可以基于频谱。

然而傅立叶变换有一个假设，那就是信号是平稳的，即信号的统计特性不随时间变化。声音信号就不是平稳信号，在很长的一段时间内，有很多信号会出现，然后立即消失。如果将这信号全部进行傅立叶变换，就不能反映声音随时间的变化。

短时傅立叶变换(short-time fourier transform)就能解决这个问题。声音信号虽然不是平稳信号，但在较短的一段时间内，可以看作是平稳的。符合直觉的解决方案是取一小段进行傅立叶变换，这也正是短时傅立叶变换的核心思想。

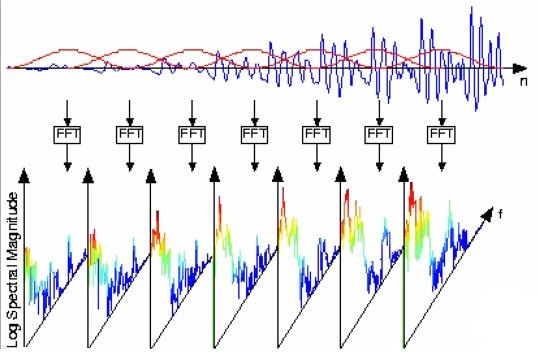
窗函数

问题还没有完全解决。从一段长的信号，截取一段信号，相当于将原始信号乘以一个方窗。方窗的傅立叶变换并不是理想的冲击函数，而是sinc函数。sinc函数除了主瓣以外，还有较高的副瓣。较高的副瓣意味着在真实频点以外，副瓣的位置上，频谱也会不为零。如果在副瓣的位置上恰好有一个幅度很小的信号，就会被完全淹没。

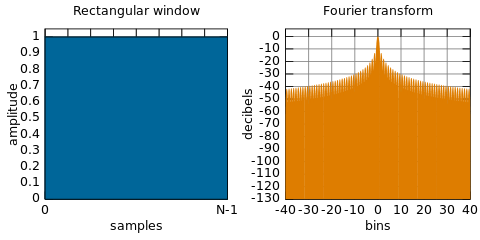
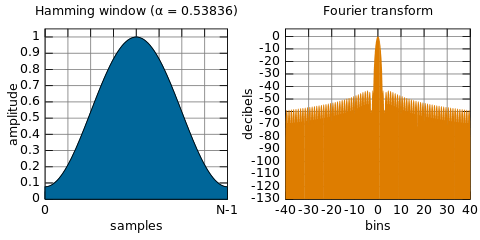
对于方窗较高的副瓣电平，解决方案是使用窗函数，代替简单地截取一段信号。通常使用的窗函数有hanning窗、hamming窗、Blackman-Haris窗等。

hamming窗的副瓣电平是-43dB，远小于方窗的副瓣电平-13dB。[1]

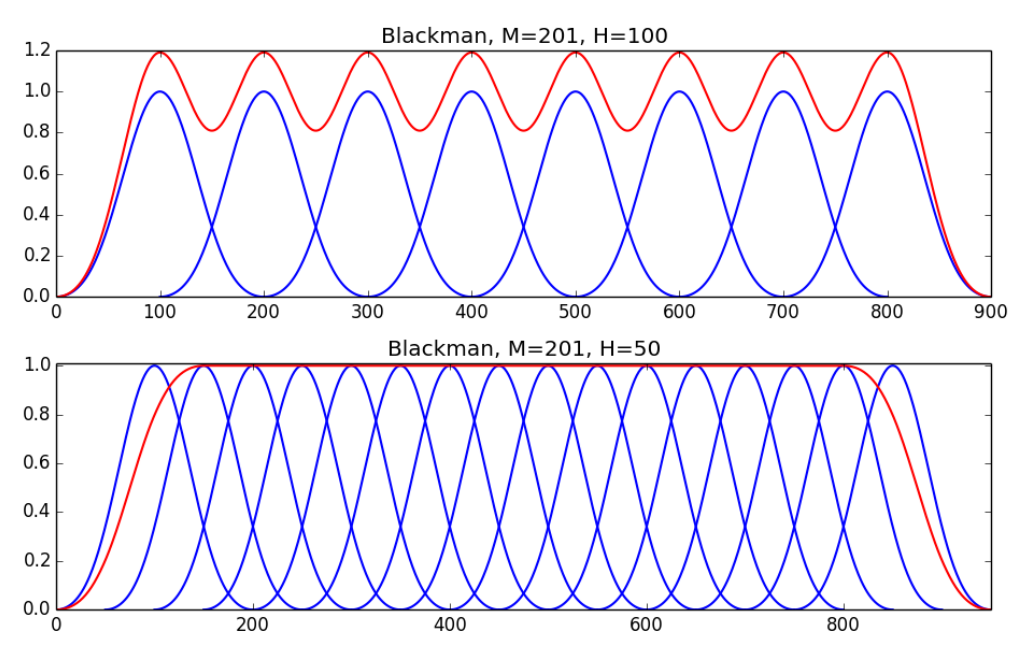
重叠区间

加窗带来了新的问题。在窗的边缘，信号会乘上一个很小的数。这意味着数据并没有充分被利用，两个相邻窗之间的信号没有完全反映到频谱当中。解决办法是两个相邻的窗有一定的重叠。通常重叠区间可以选择为窗宽度的50%或者25%。

重叠还有另一个目。信号进行短时傅立叶变换得到谱图(spectrogram)，进行一些处理之后，有时还需要恢复成为时间序列。恢复的时候必须弥补窗函数带来的影响。

hanning窗、hamming窗都是简单的正弦函数的叠加。当重叠区间较大时，窗函数的影响几乎可以忽略不计。

窗宽度的选择

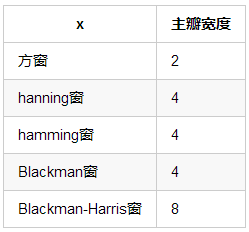
常数的傅立叶变换是冲击函数，没有宽度。窗函数的傅立叶变换都有一定宽度。方窗的主瓣宽度最小，其次是hanning窗、hamming窗。窗函数的宽度会影响频谱的分辨率。

采样频率为$f_s$的离散时间信号，快速傅立叶变换的点数为M。那么频谱，两点之间的频率之差，也就是频谱的精度为$f_s/M$。

窗函数主瓣宽度对应的真实频率为$B_s \frac{f_s}{M} Hz$

能分辨两个频率，意味着两个频率的主瓣没有重叠，即$\Delta f \ge B_s \frac{f_s}{M}$

要求快速傅立叶变换的点数：$M \ge B_s f_s / \Delta f$

其中：$B_s$为主瓣宽度

$\Delta$为以Hz为单位的频率分辨率

一般情况下，窗的宽度就取快速傅立叶变换的点数。

 

从公式中可以看出，窗函数的宽度取决于窗函数的类型，采样频率以及频率分辨率。

总结一下。选择特殊的窗函数是为了降低副瓣电平，相邻的窗之间要重叠是为了不损失时间信号的信息，窗函数的宽度一般等于快速傅立叶变换的点数，有一个下界为了保证频率分辨率。

 

[1] Characteristics of Different Smoothing Windows. http://zone.ni.com/reference/en-XX/help/371361H-01/lvanlsconcepts/char_smoothing_windows/