1. 什么是最小生成树(Minimum Spanning Trees)
对于一个无向图,如果它的所有边都带有一定的数值(即带权),则会变成下面的样子
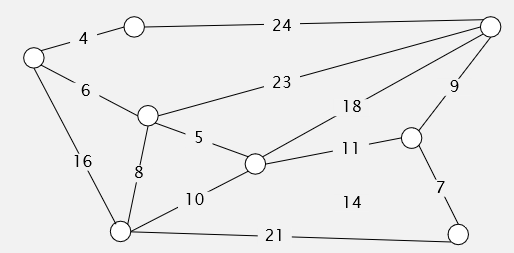
假设这些点都是城市,每个城市之间的连线代表城市间的道路,线上的数字代表着道路的长短。当然,修越长的道路就需要越多的资源。
那么如果要用最少的资源把所有城市都联系起来(即任意城市A能沿着道路抵达任意城市B),我们应该怎样建设道路呢?答案如下图:
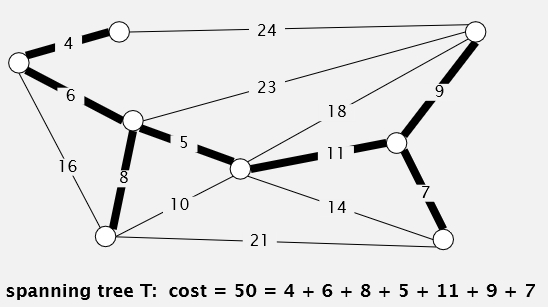
这就是最小生成树:用最小的权值总和(即数值总和)把所有点都联系起来。应注意到:最小生成树的边总数=此无向图的点总数-1。
注意,最小生成树里是不应该有闭合循环的,如:
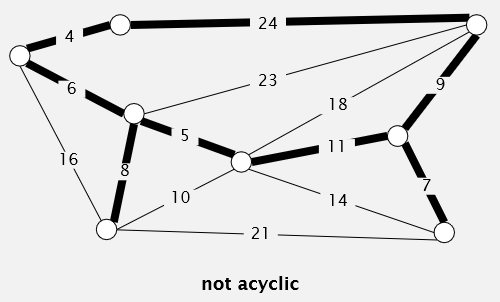
权值为24的那条边显然是多余的。
2. 生成带权的无向图
因为这种无向图只比普通无向图多了些权值,我们只需在每条边上多加一个变量来记录权值即可。
使用的邻接列表也需要把权值信息写上,如下图:

目前有两种比较主流的算法来找最小生成树:kruskal's algorithm(克鲁斯卡尔算法)和Prim's algorithm(普林演算法)。(中文译名采用音译的方法。)
接下来,我们将逐一介绍这两种算法。
3. kruskal's algorithm(克鲁斯卡尔算法)
从例子入手:
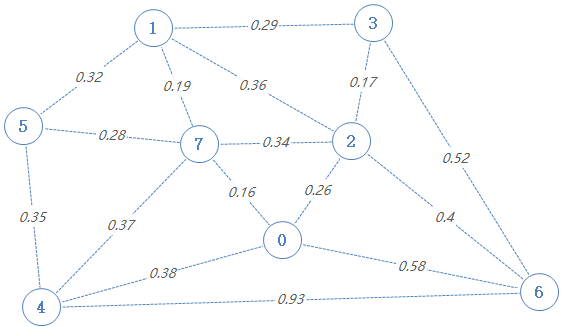
为了容易理解,我们把所有边按权值大小排成递增的数组。实际代码操作时,只需要写个方法,让数组输出一个最小值即可。
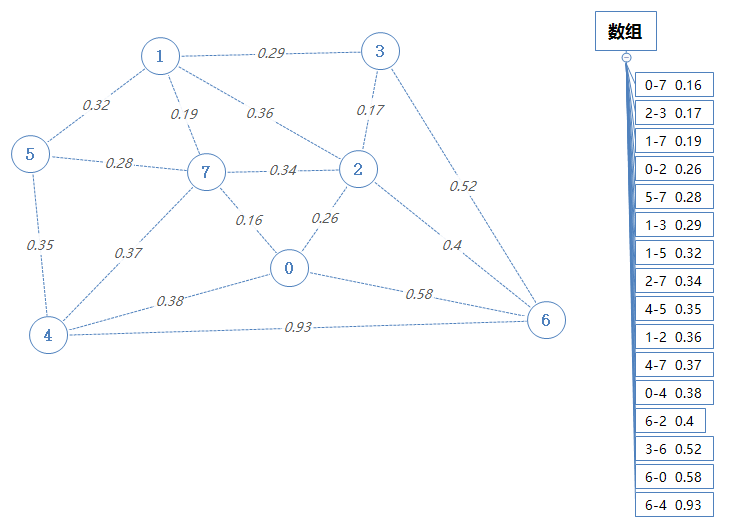
我们需要创建几个数组:
创建一个点的数组Points,把最小生成树T的点存储起来;
创建一个边的数组mst(Minimum spanning tree的简写)来把最小生成树的边都存储起来。
创建一个边的数组pq把无向图里所有的边都存储起来。
首先数组pq输出并移除一个最小值:0-7 0.16。
由于目前的最小生成树T还没有点,所以把0和7加进Points。
把0-7这条边加进mst。
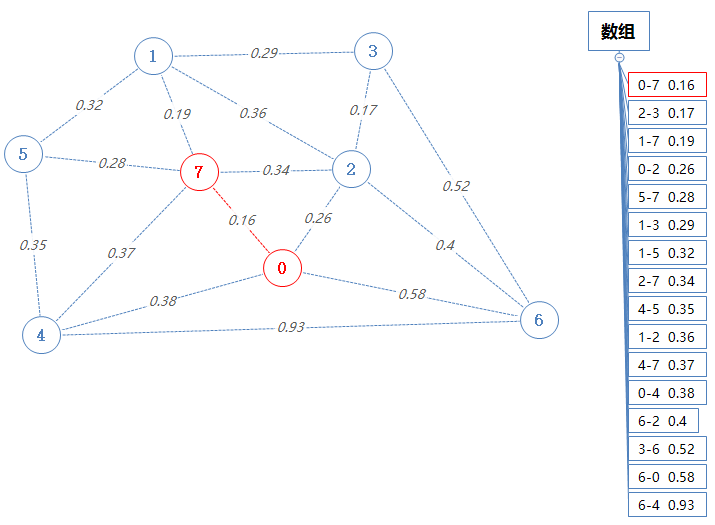
然后数组pq输出并移除一个最小值:2-3 0.17。
检查2和3是否在Points中。如果不在,则把这两个点加入到Points中。
把2-3这条边加进mst。
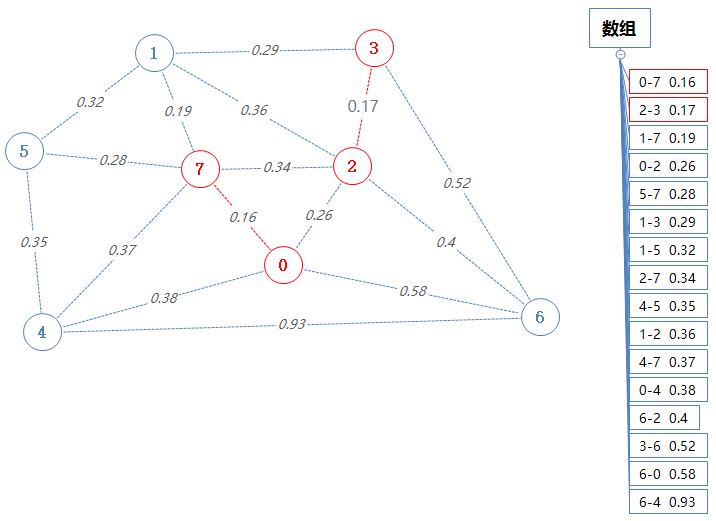
然后数组pq输出并移除一个最小值:1-7 0.19。
7已经在Points中了,只需把1加进Points里。
把1-7这条边加进mst。
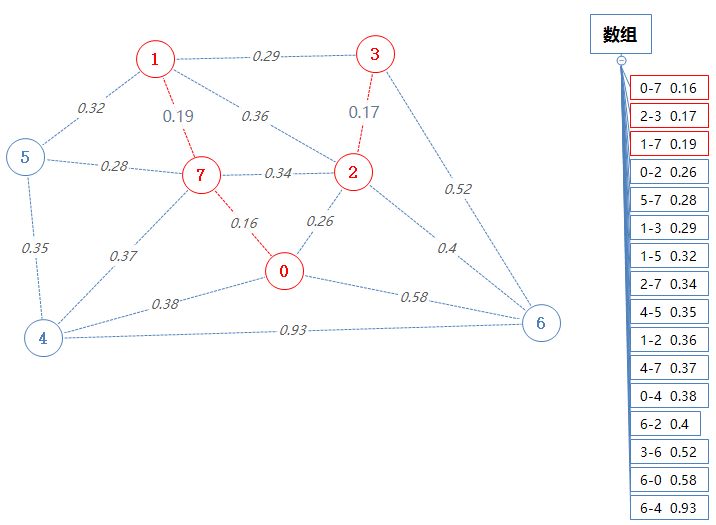
然后数组pq输出并移除一个最小值:0-2 0.26。
由于0,2都已经在Points里了,我们需要检查如果把0-2这条边加进最小生成树里是否会形成闭合循环。
检查方法稍后介绍。
如果不会形成闭合循环,则把这条边加进最小生成树T中;否则,则无视这条边,继续看下一条边。
在这里,不形成闭合循环,把0-2这条边加进mst中。
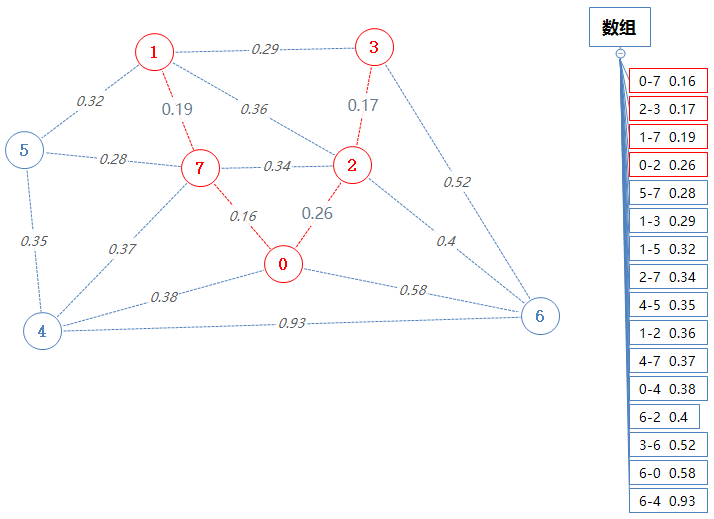
然后数组pq输出并移除一个最小值:5-7 0.28。
7已经在Points中了,只需把5加进Points里。
把5-7这条边加进mst。
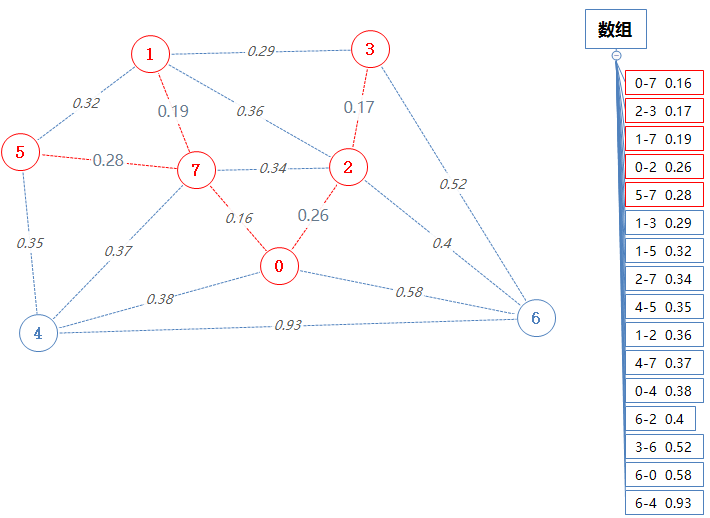
然后数组pq输出并移除一个最小值:1-3 0.29。
由于1,3都已经在Points里了,我们需要检查如果把1-3这条边加进最小生成树里是否会形成闭合循环。
会形成闭合循环,无视之。
然后数组pq输出并移除一个最小值:1-5 0.32。
由于1,5都已经在Points里了,我们需要检查如果把1-5这条边加进最小生成树里是否会形成闭合循环。
会形成闭合循环,无视之。
然后数组pq输出并移除一个最小值:2-7 0.34。
2,7都已经在Points里,且会形成闭合循环,无视之。
然后数组pq输出并移除一个最小值:4-5 0.35。
5已经在Points中了,只需把4加进Points里。
把5-4这条边加进mst。
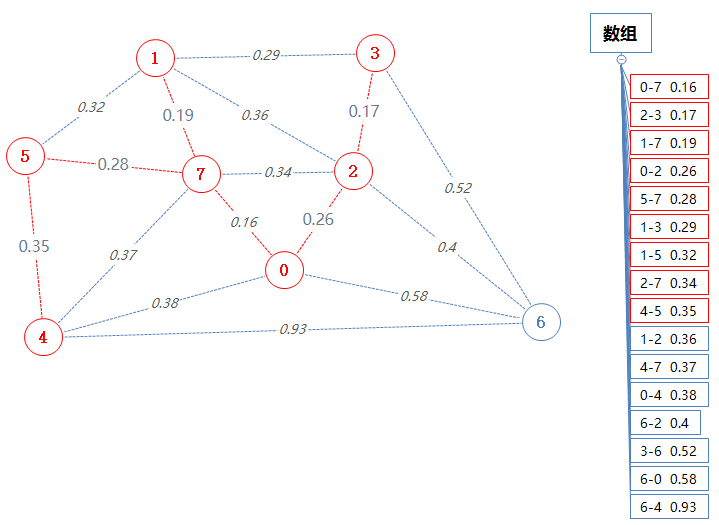
然后数组pq输出并移除一个最小值:2-1 0.36。
2,1都已经在Points里,且会形成闭合循环,无视之。
然后数组pq输出并移除一个最小值:4-7 0.37。
4,7都已经在Points里,且会形成闭合循环,无视之。
然后数组pq输出并移除一个最小值:4-0 0.38。
4,0都已经在Points里,且会形成闭合循环,无视之。
然后数组pq输出并移除一个最小值:6-2 0.4。
2已经在Points中了,只需把6加进Points里。
把6-2这条边加进mst。
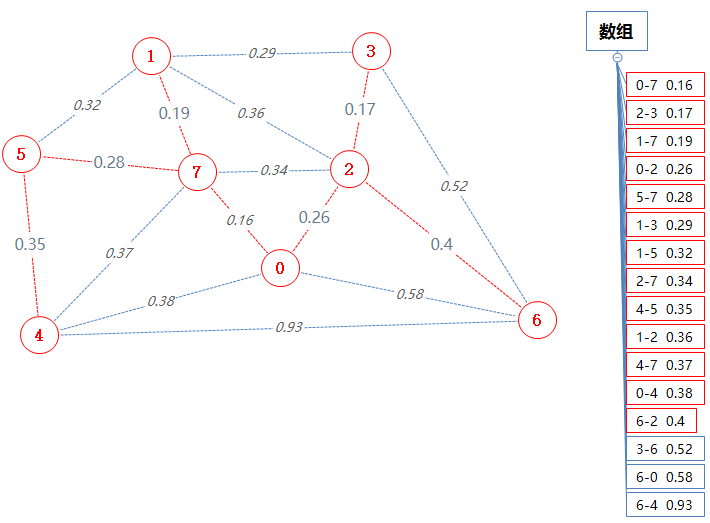
此时,mst里的边数=无向图的点总数-1。说明最小生成树已经形成了,算法结束。
现在讨论如何检测新加入的边(v-w)是否会使最小生成树形成闭合循环。假设现在最小生成树的点总数为V。
可以用深度优先搜索来检测v是否能抵达w,如果可以,说明最小生成树中已经有路连接v和w了,再加一条v-w会形成闭合循环。
但是,还有一种方法更为高效:并查集算法。简单总结一下就是:
v与和v相连的所有点形成一个区域,此区域用一个点a来代表。
w与和w相连的所有点形成一个区域,此区域用一个点b来代表。
然后对比a是否等于b,如果是,则说明v,w处于同一区域,最小生成树中已经有路连接v和w了,再加一条v-w会形成闭合循环;如果不是,说明v和w处于不同区域,可以加v-w进最小生成树。
总结一下kruskal's algorithm(克鲁斯卡尔算法)的通用思路就是:
把所有边放进一个数组里。
然后数组输出并移除一个拥有最小权值的边,如果这条边加入到最小生成树内不会形成闭合循环,则把它加进去;否则无视它。
如此循环,直到最小生成树的边总数=无向图的点总数-1为止。
顺带一提:输出数值的最小值的方法可以把此数组做出最小堆的结构,然后输出第一个元素即可。
代码大概是这样子的:

4. Prim's algorithm(普林演算法)
此算法有两种实现版本:懒惰算法版(lazy implementation)和贪心算法版(eager implementation)。
懒惰算法和贪心算法是两种思想,贪心算法也被称为过度热情算法。
从一个例子中感受一下:
假设a在他的房间里愉快地玩耍,突然他妈叫他收拾房间。此时a有两个选择:要么马上收拾,要么等会再收拾。
如果选择马上收拾,a会马上打扫房间,甚至把走廊也扫了一遍。这就是贪心算法。
如果选择等会再收拾,a会等到他妈要来检查的前一瞬间才开始收拾。这就是懒惰算法。
对于一个程序来说,贪心算法就是当程序收到一个指令时,它不但会完成指令,还会过度热情地多做点其它事情;
懒惰算法就是程序收到一个指令时,它会暂时无视之,等到我们要用到那个指令生成的结果时,程序才会去做这个指令。
接下来,逐一介绍这两个实现版本:
普林演算法之懒惰实现版本
从例子入手:
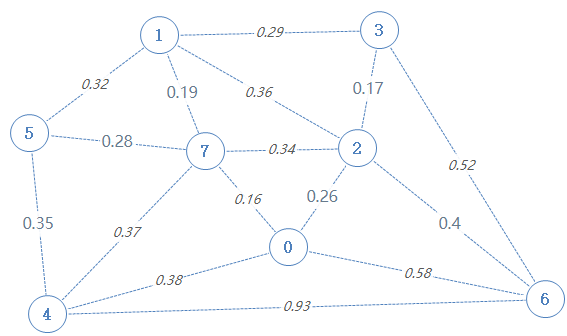
我们需要创建几个数组:
创建一个点的数组Points,把最小生成树T的点存储起来;
创建一个边的数组mst(Minimum spanning tree的简写)来把最小生成树的边都存储起来。
创建一个边的数组pq。
首先,随便找一个点开始:如0.
把0加入到Points里,把含点0的所有边加入到pq里。(为了方便理解,这里的边按权值递增排进数组,实际操作只需从数组中输出最小值,不必排序)
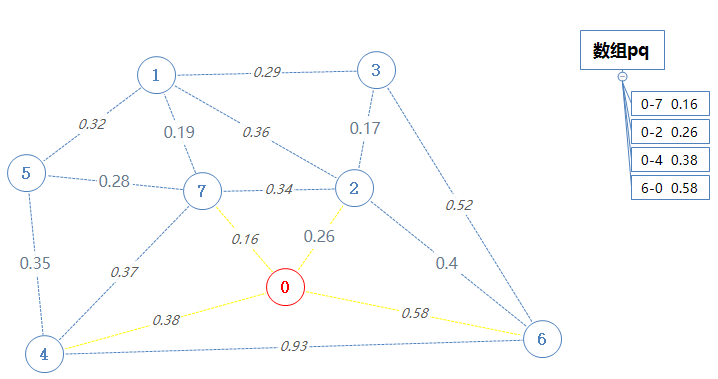
然后pq输出并移除最小一个最小值:0-7 0.16。
0已经在Points中了,只需把7加进Points里。
把含点7的除了边的另一个端顶点已经在Points里之外的所有边加入到pq里。

然后pq输出并移除最小一个最小值:1-7 0.19。
7已经在Points中了,只需把1加进Points里。
把含点1的除了边的另一个端顶点已经在Points里之外的所有边加入到pq里。
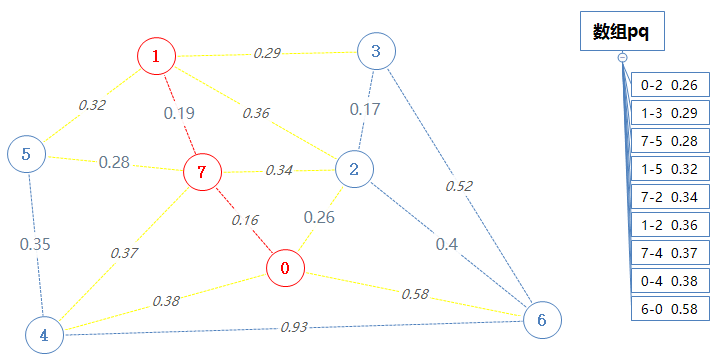
然后pq输出并移除最小一个最小值:0-2 0.26。
0已经在Points中了,只需把6加进Points里。
把含点2的除了边的另一个端顶点已经在Points里之外的所有边加入到pq里。

然后pq输出并移除最小一个最小值:2-3 0.17。
2已经在Points中了,只需把3加进Points里。
把含点3的除了边的另一个端顶点已经在Points里之外的所有边加入到pq里。
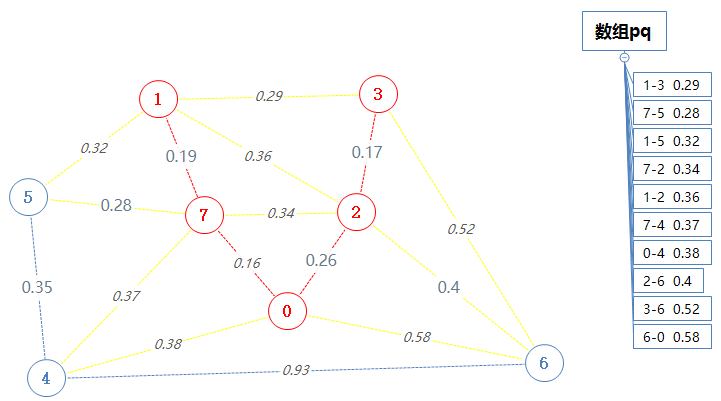
然后pq输出并移除最小一个最小值:1-3 0.29。
3,1都已经在Points里,无视之。
然后pq输出并移除最小一个最小值:7-5 0.28。
7已经在Points中了,只需把5加进Points里。
把含点5的除了边的另一个端顶点已经在Points里之外的所有边加入到pq里。

然后pq输出并移除最小一个最小值:1-5 0.32。
5,1都已经在Points里,无视之。
然后pq输出并移除最小一个最小值:7-2 0.34。
7,2都已经在Points里,无视之。
然后pq输出并移除最小一个最小值:4-5 0.35。
5已经在Points中了,只需把4加进Points里。
把含点4的除了边的另一个端顶点已经在Points里之外的所有边加入到pq里。

然后pq输出并移除最小一个最小值:1-2 0.36。
2,1都已经在Points里,无视之。
然后pq输出并移除最小一个最小值:7-4 0.37。
7,4都已经在Points里,无视之。
然后pq输出并移除最小一个最小值:0-4 0.38。
0,4都已经在Points里,无视之。
然后pq输出并移除最小一个最小值:2-6 0.4。
2已经在Points中了,只需把6加进Points里。
把含点6的除了边的另一个端顶点已经在Points里之外的所有边加入到pq里。(没有可加的边)

此时,mst里的边数=无向图的点总数-1。说明最小生成树已经形成了,算法结束。
这个算法懒惰在哪呢?我们沿用那个收拾房间的例子。
总结一下通用思路:
1. 首先随便选一个点加进Points
2. 然后把含此点的除了边的另一个端顶点已经在Points里之外的所有边加入到pq里。(孩子a听到要收拾房间,就把东西全部塞到房间里了)
3. 然后pq输出并移除最小一个拥有最小值权值的边,如果此边的另一端点在Points里,则无视之;如果不在,则把此点加进Points里。(a的妈妈要来查房了,马上收拾。)
4. 重复2,3步直到mst里的边数=无向图的点总数-1。
代码实现:


普林演算法之贪心实现版本
从例子入手:

我们需要创建几个数组:
创建一个点的数组Points,把最小生成树T的点存储起来;
创建一个边的数组mst(Minimum spanning tree的简写)来把最小生成树的边都存储起来。
创建一个点的数组pq。
首先,随便找一个点开始:如0.
把0加入到Points里,把点0能直接去的点加入到pq里。(为了方便理解,这里的边按权值递增排进数组,实际操作只需从数组中输出最小值,不必排序)
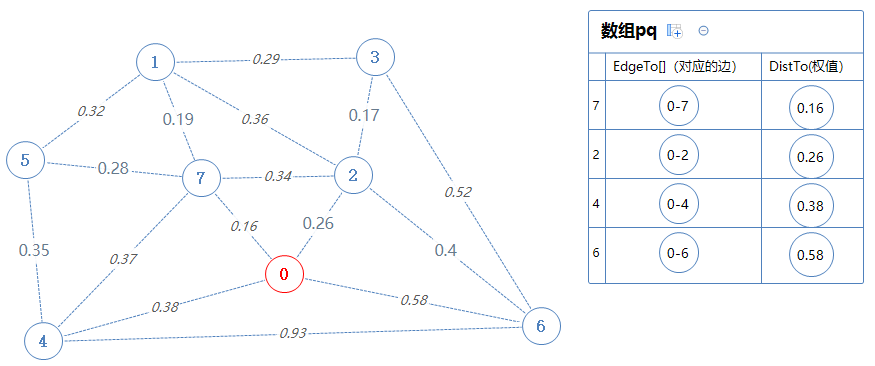
然后数组输出并移除最小值:7. 把7对应的边7-0加入到mst里,把7加入Points里。
点7能直接去的、不在Points里的点(1,2,5,4)加入到pq,但是2,4已经在pq里了,7-2的权值0.34比pq里面的0-2的权值大,故无视之;7-4的权值0.34比pq里面的0-4的权值大,故无视之。
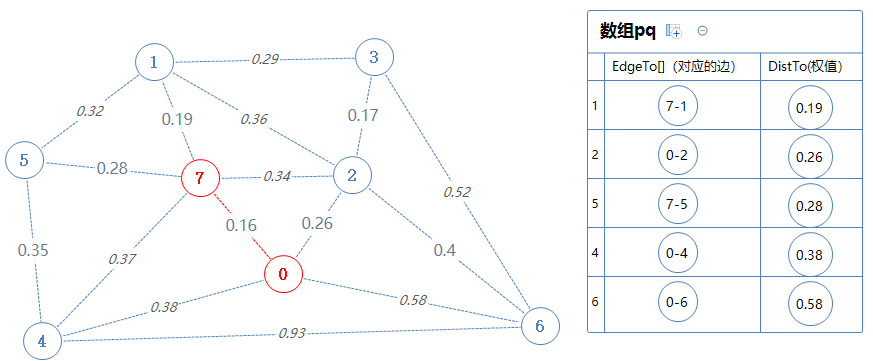
然后数组输出并移除最小值:1. 把1对应的边7-1加入到mst里,把1加入Points里。
点1能直接去的、不在Points里的点(3,2,5)加入到pq,但是2,5已经在pq里了,1-2的权值0.36比pq里面的0-2的权值大,故无视之;1-5的权值0.32比pq里面的7-5的权值大,故无视之。
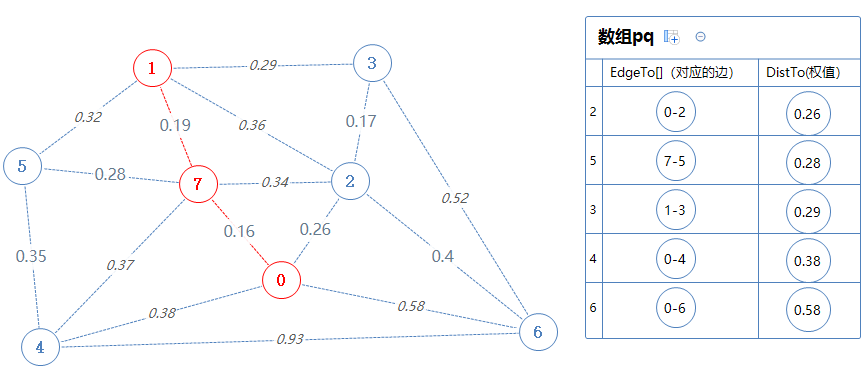
然后数组输出并移除最小值:2. 把2对应的边0-2加入到mst里,把2加入Points里。
点2能直接去的、不在Points里的点(3,6)加入到pq,但是3,6已经在pq里了,3-2的权值0.17比pq里面的1-3的权值小,故取代之;6-2的权值0.4比pq里面的0-6的权值小,故取代之。
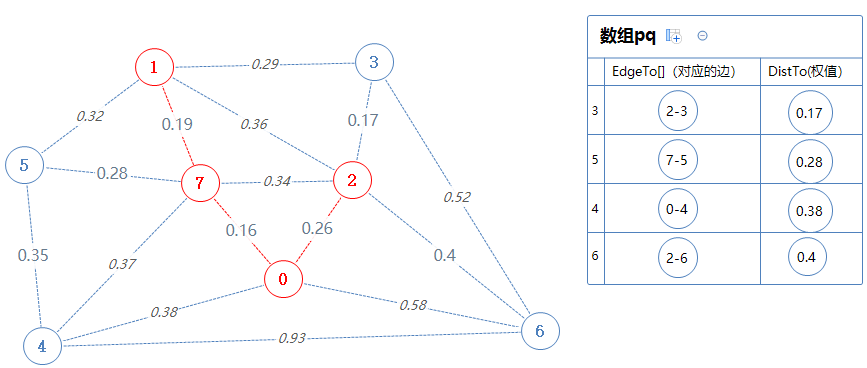
然后数组输出并移除最小值:3. 把3对应的边2-3加入到mst里,把3加入Points里。
点3能直接去的、不在Points里的点(6)加入到pq,但是6已经在pq里了,3-6的权值0.52比pq里面的6-2的权值大,故无视之。

然后数组输出并移除最小值:5. 把5对应的边7-5加入到mst里,把5加入Points里。
点5能直接去的、不在Points里的点(4)加入到pq,但是4已经在pq里了,5-4的权值0.35比pq里面的0-4的权值小,故取代之。
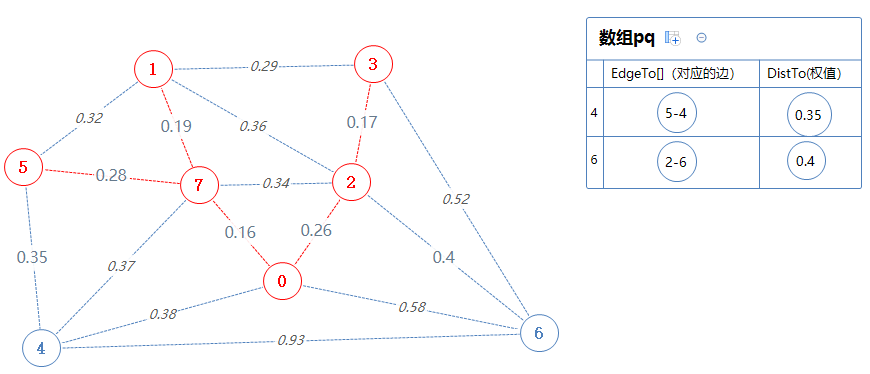
然后数组输出并移除最小值:4. 把4对应的边5-4加入到mst里,把4加入Points里。
点4能直接去的、不在Points里的点(6)加入到pq,但是6已经在pq里了,4-6的权值0.93比pq里面的6-2的权值大,故无视之。

然后数组输出并移除最小值:6. 把6对应的边6-2加入到mst里,把6加入Points里。
点6没有能直接去的、不在Points里的点。最小生成树生成完毕,结束算法。

总结一下通用思路:
1. 首先随便选一个点加进Points。
2. 然后把这个点能直接去的、不在Points里的点加入到数组pq中,把对应的那些边记录下来。如果要加的点已经存在于pq中,则看新加入的对应的边权值是否比已存在的小,如果是则取代之;否则无视之。
3. 数组输出并移除拥有最小值的点,把这个点加进Points,这个点对应的边加进mst里。
4. 重复2-3步,直到pq没有元素为止。
这个算法贪心在哪?
与懒惰版对比一下就很显然了: 第二步,懒惰版是直接把所有边塞进数组里,而贪心版是全部逐一比较(a会马上打扫房间,甚至把走廊也扫了一遍)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号