银行风险控制模型的对比

银行风险控制模型

一：读取数据

import pandas as pd
inputfile = 'E:/python/bankloan.xls'
data = pd.read_excel(inputfile)
print (data.head())

 

逻辑回归模型~sklearn

X = data.drop(columns='违约')
y = data['违约']
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)

model = LogisticRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(y_pred)

 

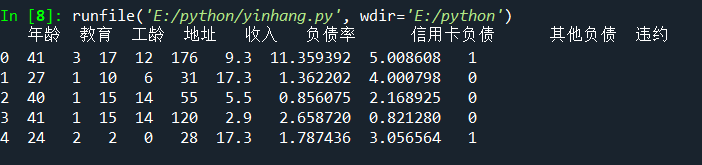
准确率与混淆矩阵

from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)

 

 

 

混淆矩阵

def cm_plot(y, y_pred):
  from sklearn.metrics import confusion_matrix #导入混淆矩阵函数
  cm = confusion_matrix(y, y_pred) #混淆矩阵
  import matplotlib.pyplot as plt #导入作图库
  plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
  plt.colorbar() #颜色标签
  for x in range(len(cm)): #数据标签
    for y in range(len(cm)):
      plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
  plt.ylabel('True label') #坐标轴标签
  plt.xlabel('Predicted label') #坐标轴标签
  return plt
cm_plot(y_test, y_pred)

 

 

 

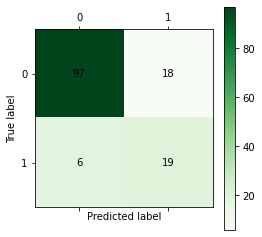
BP神经网络~Keras

import pandas as pd 
from keras.models import Sequential
from keras.layers.core import Dense, Activation
import numpy as np
# 参数初始化
inputfile = 'E:/python/bankloan.xls'
data = pd.read_excel(inputfile)
x_test = data.iloc[:,:8].values
y_test = data.iloc[:,8].values
inputfile = 'E:/python/bankloan.xls'
data = pd.read_excel(inputfile)
x_test = data.iloc[:,:8].values
y_test = data.iloc[:,8].values

model = Sequential()  # 建立模型
model.add(Dense(input_dim = 8, units = 8))
model.add(Activation('relu'))  # 用relu函数作为激活函数，能够大幅提供准确度
model.add(Dense(input_dim = 8, units = 1))
model.add(Activation('sigmoid'))  # 由于是0-1输出，用sigmoid函数作为激活函数
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
# 编译模型。由于我们做的是二元分类，所以我们指定损失函数为binary_crossentropy，以及模式为binary
# 另外常见的损失函数还有mean_squared_error、categorical_crossentropy等，请阅读帮助文件。
# 求解方法我们指定用adam，还有sgd、rmsprop等可选
model.fit(x_test, y_test, epochs = 1000, batch_size = 10)
predict_x=model.predict(x_test)
classes_x=np.argmax(predict_x,axis=1)
yp = classes_x.reshape(len(y_test))

def cm_plot(y, yp):
  from sklearn.metrics import confusion_matrix
  cm = confusion_matrix(y, yp)
  import matplotlib.pyplot as plt
  plt.matshow(cm, cmap=plt.cm.Greens)
  plt.colorbar()
  for x in range(len(cm)):
    for y in range(len(cm)):
      plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
  plt.ylabel('True label')
  plt.xlabel('Predicted label')
  return plt
cm_plot(y_test,yp).show()# 显示混淆矩阵可视化结果
score  = model.evaluate(x_test,y_test,batch_size=128)  # 模型评估
print(score)

 

 

 两个模型对比差不多，总体来看神经网络更好一点