公告

狄拉克δ函数

Posted on 2011-12-16 20:45 无忧consume 阅读(1596) 评论(0) 收藏举报

狄拉克δ函数

狄拉克δ函数（Dirac Delta function），有时也说单位脉冲函数。通常用δ表示。在概念上，它是这么一个“函数”：在除了零以外的点都等于零，而其在整个定义域上的积分等于1。严格来说狄拉克δ函数不能算是一个函数，因为满足以上条件的函数是不存在的。但可以用分布的概念来解释，称为狄拉克δ分布，或δ分布，但与费米-狄拉克分布是两回事。在广义函数论里也可以找到δ函数的解释，此时δ作为一个极简单的广义函数出现。

在实际应用中，δ函数或δ分布总是伴随着积分一起出现。δ分布在偏微分方程、数学物理方法、傅立叶分析和概率论里都和很多数学技巧有关。

狄拉克δ函数的定义为：定义

$\delta(x-c)=0,\quad x\ne c$

$\int_a^b\delta(x-c)dx=1,\quad a<c<b$

性质

狄拉克δ函数有以下性质：

$δ( - x) = δ(x)$
$\delta^\prime(-x)=-\delta^\prime(x)$
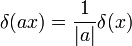
$\delta(ax)=\frac{1}{|a|}\delta(x)$
$x δ(x) = 0, x δ(x - a) = a δ(x - a)$
$\delta(x^2-a^2)=\frac{1}{2|a|}[\delta(x+a)+\delta(x-a)]$
$\int_a^b f(x)\delta(x-c)dx=f(c),\quad a<c<b$
$\int_a^b f(x)\frac{d^n}{dx^n}\delta(x-c)dx=(-1)^n[\frac{d^n}{dx^n}f(x)]_{x=c},\quad a<c<b$

表达式

狄拉克δ函数的表达式：

$\delta(x)=\lim_{\alpha\to 0^+}\frac{1}{\pi}\frac{\alpha}{\alpha^2+x^2}$
$\delta(x)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}e^{ikx}dk$
$\delta(x)=\lim_{k\to\infty}\frac{1}{\pi}\frac{\sin{kx}}{x}$

刷新页面返回顶部