读研路第一博_KNN算法推导及其代码实现

文章简介

　本文分成两个部分，一是KNN的算法推导原理，二是基于python实现代码。

　　 KNN即（K-Nearest Neighbor，KNN）在算法名称中可知道其是K最邻近邻居的意思，本是1968年由Cover 、Hart等人针对分类问题而提出的，隶属于机器学习大类中的有监督学习算法。KNN算法是惰性学习法,学习程序直 到对给定的测试集分类前的最后一刻对构 造模型。在分类时,这种学习法的计算开销 在和需要大的存储开销。总结KNN方法不 足之处主要有下几点:①分类速度慢。②属 性等同权重影响了准确率。③样本库容量 依懒性较强。④K值的确定。

算法原理

　　KNN算法的思路是: 如果一个样本在特征空间中的 k 个最相似(即特征空间中最邻近)的样本中的大多数属于某一个分类类别，则该样本也属于这个类别。通常 K 的取值比较小，不会超过 20。

　　该方法在确定分类决策上只依据最邻近的一个或者k个样本的类别来决定待分样本所属的类别。KNN方法在类别决策时，只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。即在欧氏空间中通过计算该样本点与其他相邻点之间的距离，取出K个最近距离的点，再统计这K个点所属的类别占比，按少数服从多数的原则来决定该点的类别为分类占比比例最大的类别。

算法步骤

1. 数据的预处理，将所需要处理的数据按照预定格式进行转换以及空值、异常点的清洗。
2. 计算样本点离其他点的距离，并取距离最近的K个点。
3. 根据多数表决( majority-voting )规则，将未知实例归类为样本中最多数的类别。

实例解释

　　

 

 

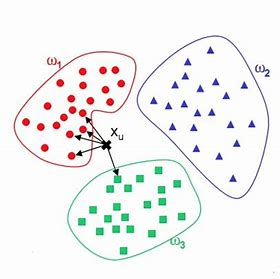
　　　　　　　　　　　　　　　　　　　　　　　　　　　　图1 二维平面数据点分布示意图

 

如图1中所示，Xu 是我们的待测样本点，此时我们在其中设K为5，也就是从Xu 出发需要计算到各个点的距离再求出距离最短的前5个点，从而可从图中看出有4个点分布在ω1中，一个点分布在ω3中，根据多数表决原则，P(ω₁)=0.8，P(ω₂)=0,P(ω₃)=0.2,因此KNN模型将认为该Xu样本点隶属于ω₁类_。

 

 

 

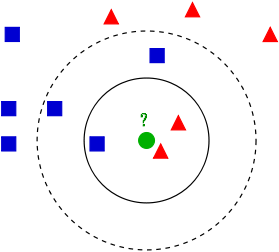
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　图2  不理想时的数据样本分布图

 

如图2中所示，我们待测样本是绿色小球，当K值较小如选择2的时候我们可以肯定地说小球隶属于三角形所属的种类，但当K值为5时，P(🔺)=2/5，而P(口)=3/5，此时就将隶属于正方形所属的类别。那么此时如何选取一个合理的K值就成了分类的关键，而因此我们将引出KNN算法的优点与缺点。

 

优点与缺点

　　优点

1. 如上述例子而言，KNN有着最简单，直接的机器学习算法之称，就是因为其算法实现简单，只需要简单的遍历计算样本点到其他点之间的欧氏距离（也可以是其他统一距离标准）即可进行排序选取前K个数据点进行分布计算，并取不同类别的概率最大值即可。

2.  适用于多分类问题，且无需估计参数，只需合理的调整K值大小即可。 

　　缺点

1. 所有样本点的距离都需要计算一次，效率较低，不适合大量样本时使用。
2. 样本标签比例不平衡时容易导致样本点类别判断失衡，而变得不合理。

算法注意事项

1. 如果当K的取值过小时，一旦有噪声得成分存在们将会对预测产生比较大影响，例如取K值为1时，一旦最近的一个点是噪声或异常点，那么就会出现偏差，K值的减小就意味着整体模型变得复杂，容易发生过拟合，模型的抗干扰能力，鲁棒性较差。
   
2. 如果K的值取的过大时，就相当于用较大邻域中的训练实例进行预测，学习的近似误差会增大（太远的点事实上与样本点是没有太大关联的，反而影响了最终的结果导致误差较大）。这时与输入目标点较远实例也会对预测起作用，使预测发生错误。K值的增大就意味着整体的模型变得简单。（可以理解K值取到等于N的时候那么模型就是遍历所有点，此时模型就是一个没有意义的最大分布概率计算公式了）
3. 如果K==N的时候，那么就是取全部的实例，即为取实例中某分类下最多的点，就对预测没有什么实际的意义了。
4. K的取值尽量要取奇数，以保证在计算结果最后会产生一个较多的类别，如果取偶数可能会产生相等的情况，不利于预测。（很好理解，奇数=偶数+奇数，当K=奇数时，如果是二分类问题，则必然存在一个偶数和一个奇数两相比较，也必然存在一个更大的值）
5. K的取法常用的方法是从k=1开始，使用检验集估计分类器的误差率。重复该过程，每次K增值1，允许增加一个近邻。选取产生最小误差率的K。
6. 一般K的取值不超过20，上限是n的开方，随着数据集的增大，K的值也要增大。

基于Python的demo实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
import seaborn as sns
iris=pd.read_csv('iris.csv') #打开数据集
iris

　　

 

　　　　　　　　　　　　图3 数据概述

 

 

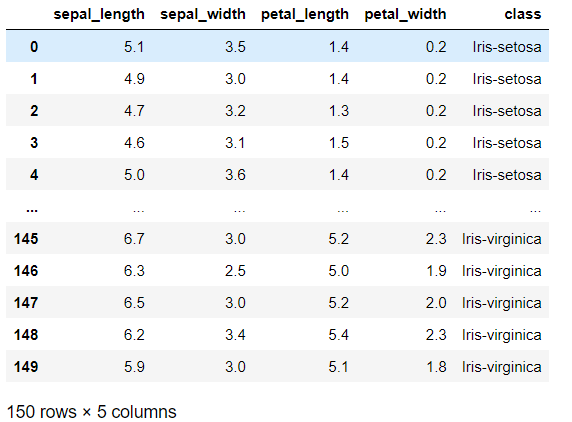
#将class进行标签编码
iris['class']=iris['class'].astype('category') #将class转为category类别
iris['class']=iris['class'].cat.codes # 将category类别进行标签转码
iris #展示结果

　　

 

　　　　　　　　　　　　图4 数据标签编码

 

 

　　

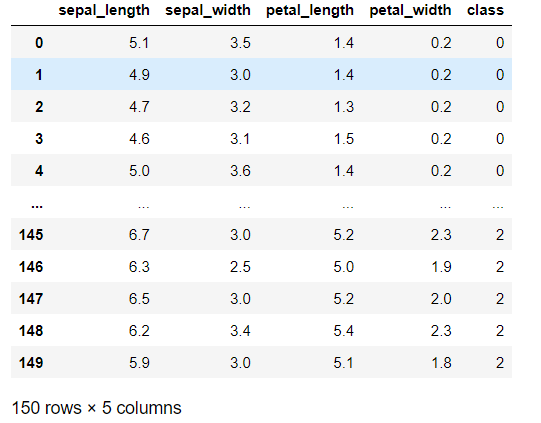
#查看数据集的相关性，进行特征筛选
#fig,ax=plt.subplots(figsize=(12,9))
iris_corr= iris.corr()
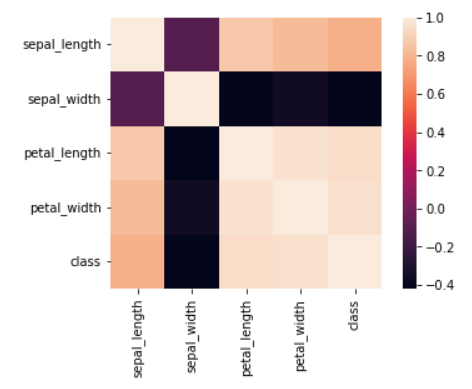
sns.heatmap(iris_corr,square=True)
#通过相关性系数的热力图可视化不难发现sepal_width与class分类之间的相关性为负，因此考虑将其删除
iris=iris.drop('sepal_width',axis=1)

　　

 

　　　　　　　　　　　　图5 相关系数热力图

 

 

from mpl_toolkits.mplot3d import Axes3D
from collections import Counter
iris.sample(frac=1).reset_index(drop=True) #打乱数据集
iris_0=iris[iris['class']==0].values
iris_1=iris[iris['class']==1].values
iris_2=iris[iris['class']==2].values #将pandas.dataframe 结构数据分类后转为 matrix
fig = plt.figure() # 创建一个画布figure，然后在这个画布上加各种元素。
ax = Axes3D(fig) # 将画布作用于 Axes3D 对象上。
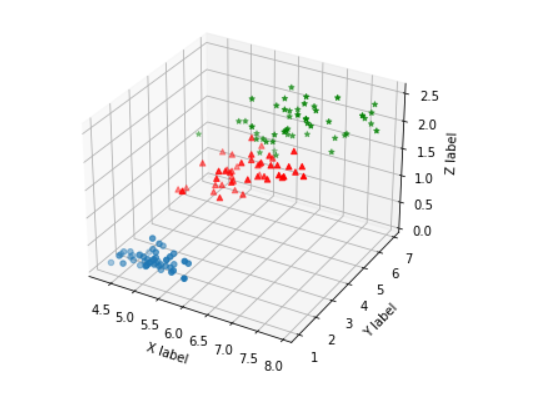
ax.scatter(iris_0[:,0],iris_0[:,1],iris_0[:,2]) # 画出散点图。
ax.scatter(iris_1[:,0],iris_1[:,1],iris_1[:,2],c='r',marker='^')
ax.scatter(iris_2[:,0],iris_2[:,1],iris_2[:,2],c='g',marker='*')
ax.set_xlabel('X label') # 画出坐标轴
ax.set_ylabel('Y label')
ax.set_zlabel('Z label')

plt.show()

　　

 

 　

　　　　　　　　　　　　图6 mpl包实现3D可视化

 

def distance(point1,point2):
    distance=sum((x1-x2)**2 for x1,x2 in zip(point1,point2))**0.5
    return distance

def train_test_split():
    train_len = int(len(iris) * 0.7)
    test_len = int(len(iris) * 0.3)

    # split the dataframe
    idx = list(iris.index)
    random.shuffle(idx)  # 将index列表打乱
    df_train = iris.loc[idx[:train_len]] #训练集
    df_test = iris.loc[idx[train_len:train_len+test_len]] #测试集
    # output
    df_train.to_csv('iris_train.csv')
    df_test.to_csv('iris_test.csv')

def KNN(dataset):
    #第一步整理数据集，但数据集已经处理好了
    #第二步，设立K值，此处采用循环遍历确定最优K值，而K值最好不大于N的开方，此处N为150，K值小于等于12
    dataset=dataset.sample(frac=1).reset_index(drop=True) #打乱数据集
    for k in range(1,int(math.sqrt(dataset.shape[0]))):
        flag=0
        accurate=0
        
        
        for i in range(0,len(dataset)):
            df_box=pd.DataFrame(columns=['distance','class']) #建立一个新表
            for j in range(0,len(dataset)):
                if(i!=j):
                    df_box.loc[j,'distance']=distance(dataset.iloc[i,:-1],dataset.iloc[j,:-1]) #将计算出的欧氏距离存入
                    df_box.loc[j,'class']=dataset.iloc[j,-1]   #将每一个计算的点class存入
                else: 
                    df_box.loc[j,'distance']=99999 #遇到自己无限大
                    df_box.loc[j,'class']=dataset.iloc[i,-1]  #遇到自己跟自己同类
                    #list1.append(distance(iris.iloc[i,:-1],iris.iloc[j,:-1]))
                    #list2.append(iris.iloc[j,-1])
                
            
            df_box=df_box.sort_values(by='distance')
            if(max(Counter(df_box.loc[:k,'class']).keys(),key=Counter(df_box.loc[:k,'class']).get)==dataset.iloc[i,-1]):
                #计算前K个class类中出现次数最多的class并取出该key值，再与自身的真实类别进行判别 如果正确则+1
                flag+=1
        
        accurate=flag/len(dataset) #计算准确率
        #df_box.to_csv('df_box.csv')
        print("***************K等于",k,"时,准确率为",round(accurate*100,2),'%')
        

if __name__ == "__main__":
    KNN(iris)

　　

　

　　　　　　　　　　　　图7 最终结果

不难发现最终我们将选择K为2或4作为KNN模型的预设参数，在考虑K值较小容易被噪声影响时，我们可选择K=4作为最终参数，两者的运行时间级别在一个数量级，同时K=4的模型抗干扰能力会更强一点。