残差神经网络的短路原理

起因：深度网络的退化问题

从经验来看，网络的深度对模型的性能至关重要，当增加网络层数后，网络可以进行更加复杂的特征模型的提取，所以当模型更深时，理论上可以取得更加好的结果，但实践中发现，随着网络深度的增加，模型的性能出现了退化的情况。随着网络深度的增加，参数增多，网络变得难以训练，且在训练过程中伴随着梯度消失或梯度爆炸的现象出现，因此单纯的靠叠加层数来提升网络的效果在实际中并不总是有用的甚至还有可能出现反效果。

解决方案之一：残差学习

深度网络的退化问题至少说明深度网络的并不容易训练，但考虑这样一个事实：现在有一个浅层网络，你想通过堆叠新层来建立深度网络，一个极端的情况是这些增加的层不怎么学习，仅仅复制浅层网络的特征，即恒等映射。在这种情况下，深层网络的性能至少和浅层网络一样，也不应该出现退化的情况，当然这肯定是因为当前的训练方法有问题才使得深层网络无法找到合适的参数。

何凯明博士就是基于以上的思考，提出了利用残差学习来规避深度网络性能退化的问题。

对于一个堆积层结构（几个层堆积而成）当输入X时，其学习到的特征记为H(X)，现在我们希望其可以学习到残差F(X)=H(X)-X，这样其实原始的学习特征是F(X)+X。

 

 

 

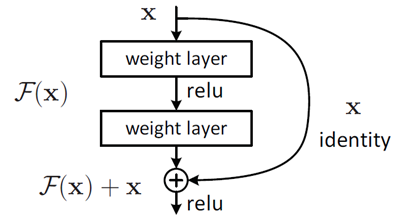
 这样做的原因是因为残差学习相比与原始特征直接学习更加容易，当残差为0时，此时堆积层仅仅做了恒等映射，至少网络的性能不会下降，实际上残差不会为0，这也会使得堆积层在输入特征基础上学习到了新的特征，从而拥有更好的性能。类似于电路中的短路，所以残差学习又称为“shortcut connection”.

残差单元可以表示为：

y_l = h(x_l) + F(x_l,W_l)

x_l+1 = f(y_l) 

其中，分别表示第l个残差单元的输入和输出。F为残差函数，表示学习到的残差，而h(xl)=xl表示恒等映射，f表示激活函数。

基于上式，我们从浅层到深层的学习特征为：

x_L = x_l+ΣF(x_i,W_i)

利用链式法则，反向传播过程中梯度为：

∂loss/∂xl =  (∂loss/∂xL)(∂xL/∂xl) = ∂loss/∂xL(1+∂(∑F(xi,Wi))/∂xL)

式中第一个因子表示损失函数的梯度，小括号中的1表示短路机制可以无损地传播梯度，而另外一项残差梯度则需要经过带有Weights的层，梯度是不会直接传播过来的。残差梯度不会那么巧全为-1，而且就算比较小，有1的存在也不会导致梯度消失。所以残差学习会更加容易。（注意上述推导并不是严格证明）。

深度网络的缺点：

（1）参数太多，当样本有限时，容易过拟合

（2）网络越大计算复杂度越高，难以应用

（3）网络越深，梯度越往后越容易消失（梯度弥散），难以优化模型

在前向传播中为了增加网络的非线性映射能力会加入激活函数，以sigmoid函数为例，当输入小于-5大于5时，输入等于1，而在-5到5之间，接近恒等映射，输入会被压缩到0-1之间，神经网络的训练利用反向传播算法来进行，其实质是导数的链式法则，就是很多偏导数连乘，导数最大为1，而且大多数数值都被推向两侧的饱和区域，这些区域的导数很小。随着网络的深度加深，导数向后传播到输入层时，就所剩无几了，基本不能引起参数W数值的扰动，这样输入层一侧的网络就学习不到新的特征了，参数得不到更新。

解决该现象的大致办法分为四种：

（1）使用更加敏感的激活函数

（2）使用层归一化

（3）在权重的初始化上下功夫

（4）调整网络的结构

重点关注第4种

highway network