数值优化(五)
共轭梯度方法
线性共轭梯度方法
线性共轭梯度方法可以用来解线性方程$$Ax=b$$其中A是正定的对称阵。这个问题等价于求解$$\Phi(x)=\frac{1}{2} xTAx-bTx$$的无约束优化问题。向量\(\{p_0,p_1,\cdots,p_i\}\)称作关于正定矩阵A相互共轭,当$$p_i^TAp_j=0 \quad \forall i \neq j$$在\(\mathbb{R}^n\)中给定一个初值点\(x_0\)和一组共轭方向\(\{p_i\}\),就可以生成一个点列$$x_{k+1}=x_k+\alpha_k p_k$$ \(\alpha_k\)是在\(p_k\)方向上的最优点,有闭式解$$\alpha_k = -\frac{r_k^T p_k}{p_k^T A p_k}$$这样的迭代步骤在最多n次后就会收敛到最优点(即线性方程的解)。关于这个事实,有如下正交情况的示意图:
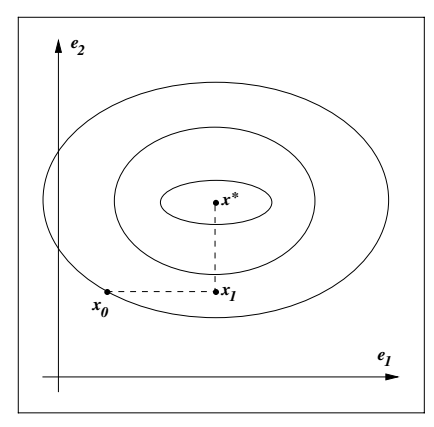
关于这一点,还有一个结论:

共轭方向
现在只需要生成一组共轭方向就可以应用上述的共轭梯度法,共轭方向的生成有多种方法,但是如果利用了共轭向量的性质,就可以只通过前一个共轭向量的信息来求解下一个共轭向量,使得在大规模问题中可以大幅度减少空间以及时间花费。具体的:$$p_k = -r_k + \beta_{k} p_{k-1}$$(其中\(r_k=Ax_k-b=\nabla f_k\))选取\(beta_k\)使得\(p_k\)与\(p_{k-1}\)共轭,就可以证明\(p_k\)也和之前的所有向量共轭。\(\beta_k\)易于得到闭式解$$\beta_k = \frac{r_k^T A p_{k-1}}{p_{k-1}^T A p_{k-1}}$$
到此,CG算法已经完整了,再利用下述定理,可以将算法进一步优化:

得到CG-Algorithm(Practical Form)
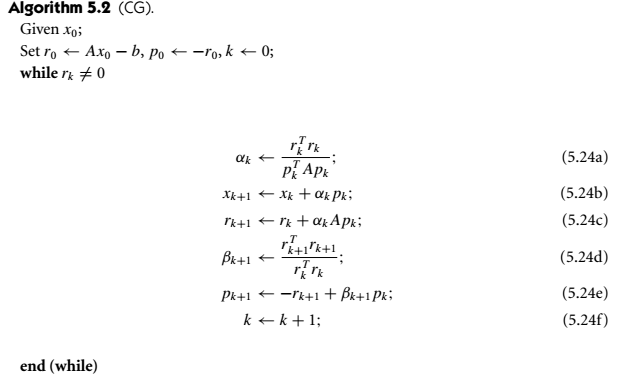



 浙公网安备 33010602011771号
浙公网安备 33010602011771号