物理深度学习（1）监督学习平均化问题

一步步推导为什么监督学习在多值输出问题中会出现“平均化”现象，以平方根反解问题为例：

🧪 问题设定（平方根反解）

p-s

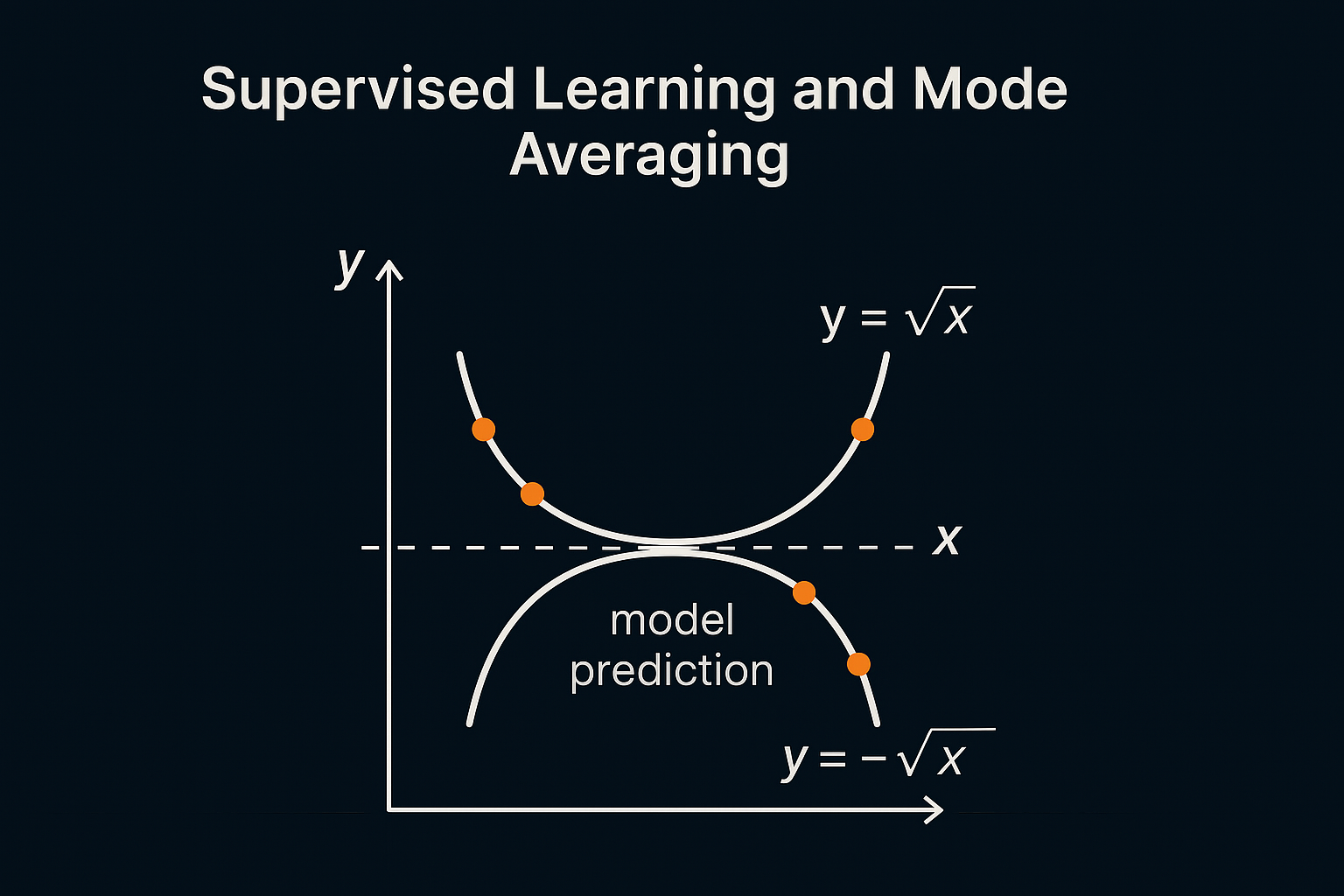
我们要学一个函数 \(f : [0,1] \rightarrow \mathbb{R}\)，满足：

\[P(f(x)) = f(x)^2 = x \]

这意味着每个 \(x \in [0, 1]\) 有两个解：

\[f^*(x) = \pm \sqrt{x} \]

训练数据是用下面方式采样的：

  • 从区间 \([0,1]\) 采样 \(x\)；
  • 随机选择 \(+\sqrt{x}\) 或 \(-\sqrt{x}\) 作为对应的 \(y\)；
  • 训练数据对：\((x, y)\) 是从这个分布中采样而来。

🎯 学习目标：最小化平均损失

监督学习中使用的是均方误差（MSE）损失函数：

\[L(f) = \mathbb{E}_{(x,y) \sim \mathcal{D}} \left[ (f(x) - y)^2 \right] \]

其中 \(\mathcal{D}\) 是上述数据分布，即 \(y = \pm \sqrt{x}\)，两者等概率。

🧮 数学推导：最优 \(f(x)\) 是条件期望 \(\mathbb{E}[y|x]\)

这一步是监督学习平均化现象的核心：

对于给定的 \(x\)，最小化 MSE 的最优函数是：

\[f^*(x) = \underset{f}{\arg\min}~ \mathbb{E}_{y|x}[(f(x) - y)^2] = \mathbb{E}[y|x] \]

这是标准平方损失下的最优预测（conditional expectation）。

现在我们具体计算一下 \(\mathbb{E}[y|x]\)：

由于 \(y = \pm \sqrt{x}\)，且两个解的概率均为 \(\frac{1}{2}\)，

所以：

\[\mathbb{E}[y|x] = \frac{1}{2} \cdot \sqrt{x} + \frac{1}{2} \cdot (-\sqrt{x}) = 0 \]

所以：

对于任意 \(x\)，期望输出为 \(f^*(x) = 0\)

这解释了为什么训练出的网络输出接近 0！

💡 从最具体的角度，一步步拆解

假设我们要学习一个函数 \(f(x)\)，输入是 \(x\)，输出是 \(y\)。我们的训练数据是很多对 \((x, y)\)，比如：

(0.25, 0.5)    ← 因为 √0.25 = ±0.5
(0.25, -0.5)
(0.36, 0.6)
(0.36, -0.6)
...

对于每个 \(x\)，可能出现两个不同的 \(y\)，但神经网络最终必须输出一个“确定的”值 \(f(x)\)。它该怎么选？

✅ 问题数学建模：监督学习最小化均方误差

神经网络通过最小化一个损失函数来训练。常见的是 均方误差（MSE）：

\[\text{Loss} = \frac{1}{N} \sum_{i=1}^{N} (f(x_i) - y_i)^2 \]

也就是说，我们想让神经网络的输出 \(f(x)\) 尽可能接近训练数据里的每个 \(y\)。

🧠 所谓“最优函数”是什么意思？

假设我们不用神经网络，而直接在纸上“算出”一个最好的 \(f(x)\)，它应该是什么？

我们来想这个问题：

对于某个固定的 \(x\)，例如 \(x = 0.25\)，训练数据中出现了两种 \(y\) 值：\(+0.5\) 和 \(-0.5\)。如果你只能选一个数 \(a\)，让它尽可能“接近”所有这些 \(y\)，你会选什么？

答案当然是中间值，也就是它们的平均值：

\[a = \frac{(+0.5) + (-0.5)}{2} = 0 \]

——这就是 \(\mathbb{E}[y|x]\)，即“给定 \(x\) 时 \(y\) 的数学期望值”。

所以，“最优函数” \(f(x)\)，在这种监督学习（MSE）下，其实就是：

💡 对于每个 \(x\)，输出 \(f(x) = \mathbb{E}[y | x]\)，也就是在训练数据中，所有对应 \(x\) 的 \(y\) 值的平均值。

🧪 举例说明：再具体一点

假设我们训练集里，\(x = 0.49\) 出现了三次，对应的 \(y\) 为：

  • \(+0.7\)
  • \(-0.7\)
  • \(+0.7\)

那么对于 \(x = 0.49\)，神经网络最佳预测应为：

\[f(0.49) = \frac{0.7 + (-0.7) + 0.7}{3} = \frac{0.7}{3} ≈ 0.233 \]

它不是 +0.7，也不是 -0.7，而是一个介于中间、既不满足原方程 \(y^2 = x\)，也不是实际出现过的解的“幻觉结果”。

🚨 为什么这是个问题？

  • 平方根问题是双解 → 训练数据是“双峰分布”；
  • 但 MSE 只会学到平均值中心点 → 模型输出不是解之一；
  • 平均值在物理、模拟、多解 PDE 中可能是“完全不合法”的值。

✅ 小结

  • “最优函数” \(f(x)\) 在监督学习 + MSE 下就是条件平均值 \(\mathbb{E}[y|x]\)；
  • 这对单峰分布（如 \(y = \sin(x)\)）是合理的；
  • 但对双峰 / 多峰问题（如 ±√x）会“平均掉所有可能”，让模型输出无意义值。

我可以帮你画出分布图（两个对称的 √x 峰）和 \(f(x)\) 平滑趋近 0 的曲线对比图。如果你觉得合适，这张图会非常适合放进那篇物理深度学习的随笔中。需要我来一张图吗？📊🧠✨

🚨 结论：监督学习在多模态下会输出不可物理解

  • 虽然真实目标是 \(\pm \sqrt{x}\)，但网络学出的却是 \(0\)；
  • \(0\) 既不是解之一，也违背了 \(f(x)^2 = x\) 的方程；
  • 这就是 “多模态平均导致的模式丢失（mode collapse）”。

🎨 可视化理解

你可以想象 y = ±√x 对应的两个“轨道”，而监督学习不加区分地把它们压扁成一条中间线 —— 而这条“中间线”根本不满足任何模式。

🧠 如何避免？

  • 使用可微分物理（DP） → 在损失中加入物理一致性
  • 使用生成模型 → 学整个条件分布 \(p(y|x)\)，输出多样结果

--end--

posted @ 2025-07-07 21:39  ffl  阅读(14)  评论(0)    收藏  举报