3-29省选集训
前言
要走了
A. 深邃
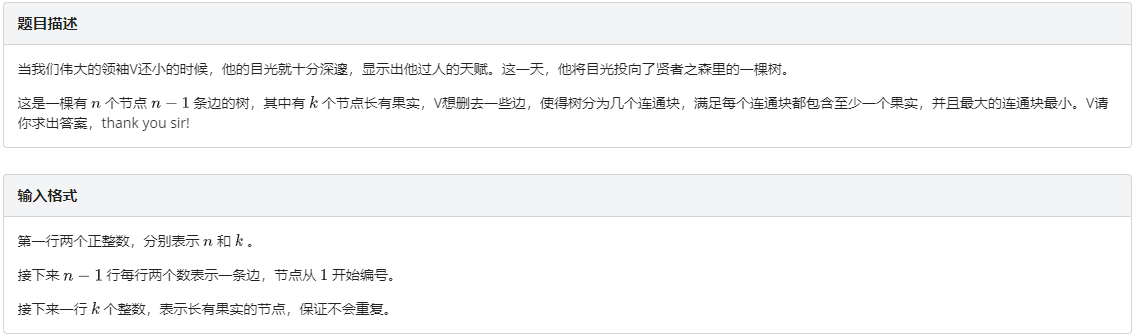
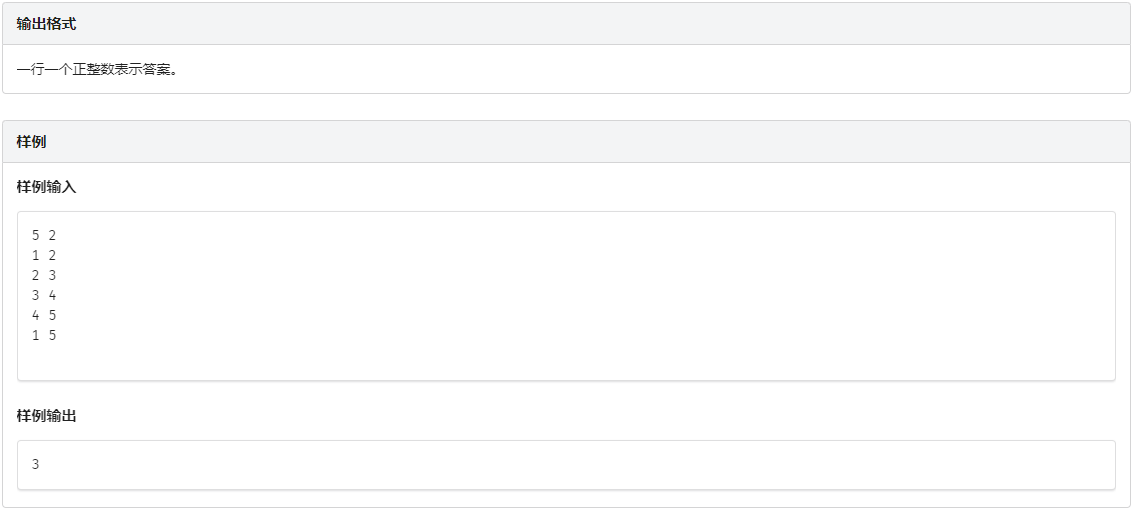
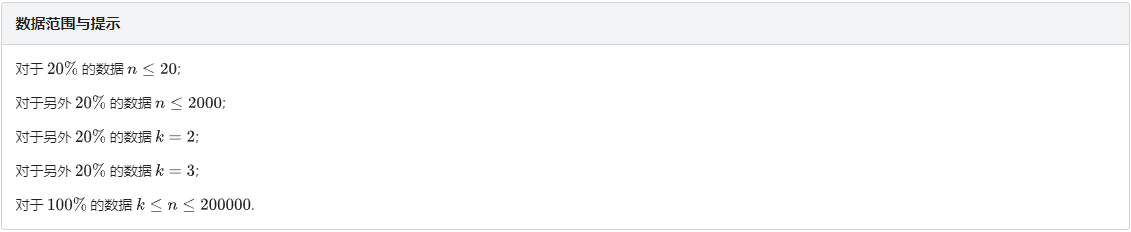
无官方题解
考场写过了
大概思路是,首先可以发现,既然最大连通块最小,那么显然是需要一个连通块里有且只有一个被选中的点,这样是最优情况
然后显然套个二分变成判定性问题
看看每个点管\(mid\)个点能不能覆盖全整棵子树
我们记录一下 \(dp[u]\) 表示以u为根的子树还剩多少个点需要其祖先来管,可以为负,代表还可以管别人
转移如下:
如果当前点\(u\)为选中的点,那么我们需要把\(u\)的儿子中 \(dp[u]>0\) 的部分从\(mid\)中扣除,然后再扣除自己的\(1\),如果转移后的\(dp[u]>0\),说明还需要祖先来管,显然不满足最优情况,不合法
如果当前点\(u\)为非选中的点,我们找儿子\(v\)中还有富余的点(即\(dp[v]<0\))中找最大的\(|dp[v]|\),然后看看能不能覆盖所有\((\sum\limits_{v\in son} dp[v]\cdot [dp[v]>0])+1\),由于需要经过\(u\)覆盖,有富余的点只能选一个
最后验证每个选中点和根即可
T1 accept
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<bitset>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn=2e5+5;
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int n,k;
bool col[maxn];
struct edge
{
int to,next;
}g[maxn<<1];
int head[maxn],cnt(0);
inline void add(int a,int b)
{
g[++cnt].to=b;
g[cnt].next=head[a];
head[a]=cnt;
return ;
}
int dp[maxn];
void dfs(int u,int fa,int tar)
{
int sum(0),mx(0);
for(int i=head[u];i;i=g[i].next)
{
int v=g[i].to;
if(v==fa) continue;
dfs(v,u,tar);
if(dp[v]>0) sum+=dp[v];
else if(dp[v]<0) mx=max(mx,(int)abs(dp[v]));
}
if(col[u]) {dp[u]=sum+1-tar; return ;}
if(mx>=sum+1) dp[u]=-(mx-sum-1);
else dp[u]=sum+1;
return ;
}
bool check(int mid)
{
for(int i=1;i<=n;i++) dp[i]=0;
dfs(1,0,mid);
if(dp[1]>0) return 0;
for(int i=1;i<=n;i++)
if(col[i]&&dp[i]>0) return 0;
return 1;
}
int main()
{
freopen("deep.in","r",stdin);
freopen("deep.out","w",stdout);
n=read(); k=read();
for(int i=1;i<n;i++)
{
int u,v;
u=read(); v=read();
add(u,v); add(v,u);
}
for(int i=1;i<=k;i++) {int x=read(); col[x]=1;}
int l=1,r=n,ans(0);
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
printf("%d\n",ans);
return 0;
}
B. 排序



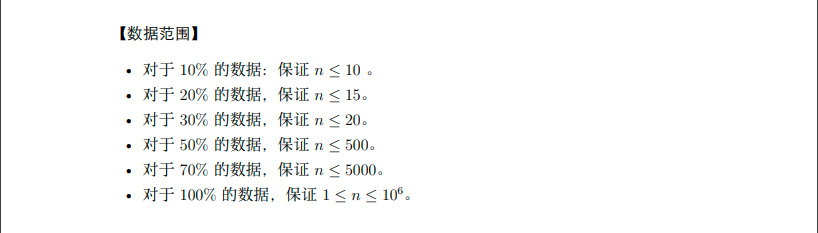
官方题解:

首先我们发现,这是一道诈骗题
因为手玩一下能够发现,每次交换的数都是确定的,说明\(p_i=c_i\)
然后考虑\(c_i\)怎么算
所谓前缀最小值,就是类似于单调队列维护的单调递减区间
我们交换的次数就是这个单调队列的元素个数
考虑到第\(i\)轮试炼,我们会经过一系列交换操作找到最小的值,放到\(i\)位置,由于是个排列,说明\([i+1,n]\)中只有\([i+1,n]\)的元素,且前\(i-1\)个数都是排好序的
\(i\)次试炼前

我们考虑\(i\)次试炼之后会怎么样:
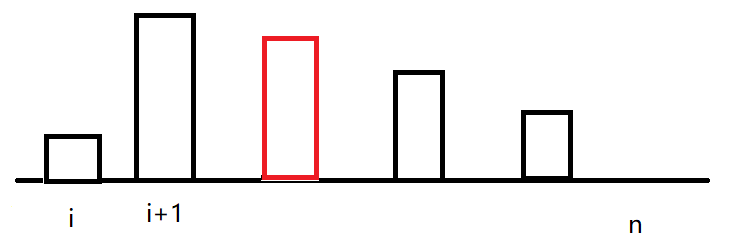
实际上,我们如果看\(i\rightarrow n\)的前缀最小值,就是这样:
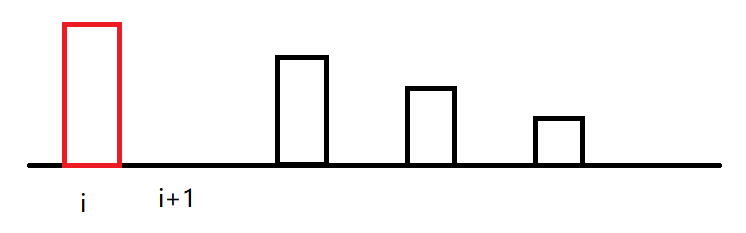
那么试炼后也就变成了:
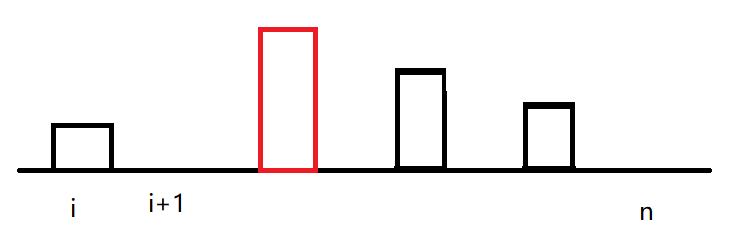
可以发现每次试炼后,相当于\(i\rightarrow n\)的前缀最小值整体向右平移了一位
设第\(i\)次试炼交换了\(c_i\)次
那么一共有\(c_i+1\)个元素参与交换
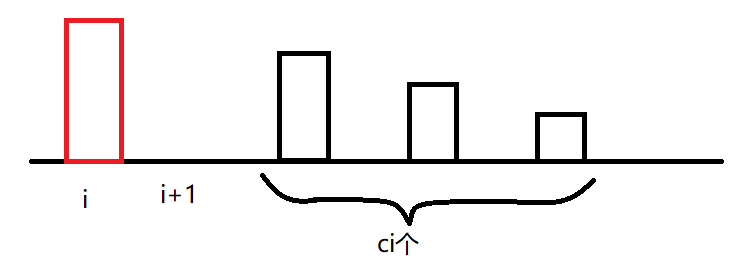
由于是向右平移,我们考虑到这\(c_i\)个数将成为第\(i+1\)轮试炼的前缀最小值的一部分
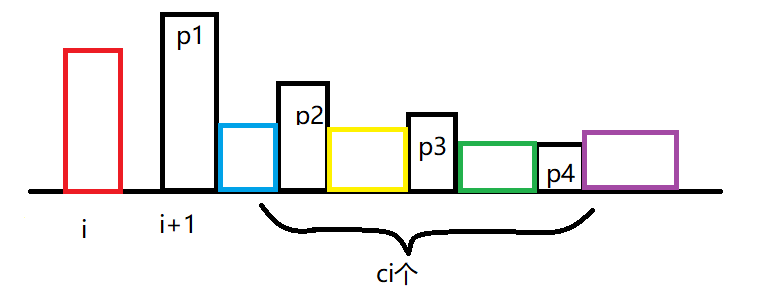
我们知道蓝色的位置的数是大于\(a_{p_1}\)的,黄色的位置的数是大于\(a_{p_2}\)的,绿色的位置的数是大于\(a_{p_3}\)的,蓝色的位置的数是大于\(a_{p_4}\)的
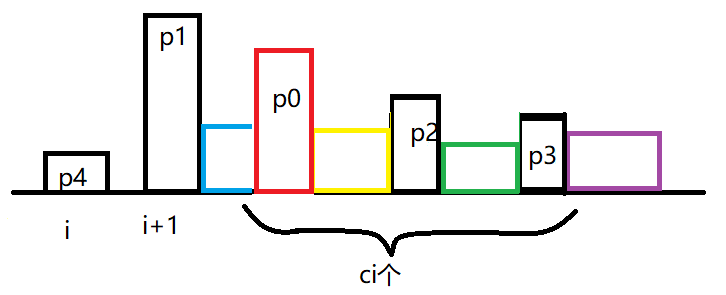
我们发现黄色位置上的数\(>a_{p_2}\),但是在\(p_2\)前面,如果\(<a_{p_0}\)的话,是可以出现在第\(i+1\)轮的前缀最小值里面的
同理,绿色位置上的数如果\(>p_2\)且\(<a_{p_2}\),也可以出现在前缀最小值里面
而所有前缀最小值的个数是\(c_{i+1}\)
那么显然\(c_{i+1}\geq c_i\)
现在考虑答案怎么算
由于给出了\(c_{i+1}\),我们想要推回第\(i\)轮的情况
由于我们可以在蓝黄绿紫这些空隙里面插入满足条件的数
那么我们倒推相当于在把\(c_{i+1}+1\)个数里面挑\(c_i+1\)个数,由于是倒推,最终要放在\(i\)位置的数是确定的,就是\(i\),我们只需要\(C_{c_{i+1}+1}^{c_i}\)随便找出\(c_i\)个数,然后显然有一种排列可以满足
因此答案就像题解所说
T2 accept
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<bitset>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn=1e6+5;
const int mod=998244353;
#define int long long
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int T,n,m,p,k;
int a[maxn],fac[maxn];
int inv[maxn];
int quick_pow(int a,int b)
{
int ans=1,tmp=a;
while(b)
{
if(b&1) ans=ans*tmp%mod;
tmp=tmp*tmp%mod;
b>>=1;
}
return ans;
}
int C(int n,int m)
{
if(!m) return 1;
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
signed main()
{
freopen("sort.in","r",stdin);
freopen("sort.out","w",stdout);
n=read();
fac[0]=1;
for(int i=1;i<=n+1;i++) fac[i]=fac[i-1]*i%mod;
inv[n+1]=quick_pow(fac[n+1],mod-2);
for(int i=n;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
for(int i=1;i<n;i++) a[i]=read();
int ans=1;
for(int i=1;i<=n-2;i++)
ans=ans*C(a[i+1]+1,a[i])%mod;
printf("%lld\n",ans);
return 0;
}
C. 方格


官方题解:


首先我们发现,每次一个位置\((i,j)\)翻转会涉及到四个位置\((i,j),(i,m-j+1),(n-i+1,j),(n-i+1,m-j+1)\),我们称这四个位置为一个组
我们发现,对于一个位置\(i,j\),依次翻转\(i\)行和\(j\)列,一定要依次翻转
会发现\((i,j),(i,m-j+1),(n-i+1,j)\)依次在轮换
由于我们发现,每次都是这三个位置上的东西在轮换排列
然后对于任意位置都可以进行轮换其对应的三个位置
我们手玩一下发现,这样一个组可以任意变成任何一个偶排列(逆序对数为偶数),因为每次翻转是三个元素,三个元素不论怎么翻转逆序对数都是偶数,因此无论翻转多少三元组都是偶排列
有一种特殊情况:
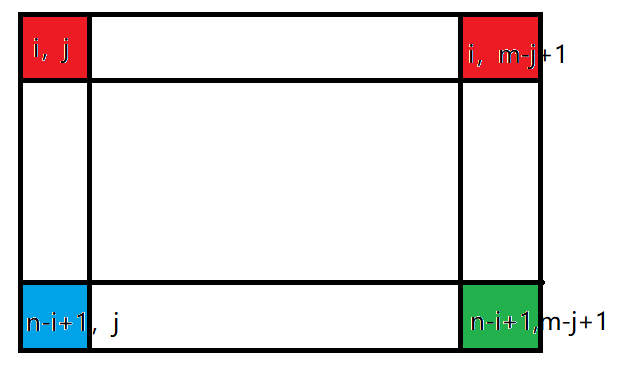
颜色相同代表上面字母相同
如果有两个点相同,可以达到奇排列
可以认为,如果有相同的话,就会影响到逆序对数的奇偶
也就是说,如果一个组里有超过一对相同的数,是可以通过轮换形成任意排列的
这样记得用\(4!\)除掉每种颜色的排列就是这一组的答案
否则一组内四个数都不同的话就只能形成12种排列了(所有偶排列)
如果我们设组数为\(x\),那么这部分对答案的贡献就是\(12^x\)
然后考虑,如果我们初始的时候进行一次交换,那么那些只能到达偶排列的情况就变成了只能到达奇排列
我们发现,按照题解那样建图,建出行和列的二分图,相当于求边的染色方案数
会找到若干连通块,我们把某个连通块抽出一颗生成树
我们钦定这颗生成树中的一个点,设为\(u\),如果我们把所有点的颜色都异或\(1\),边的染色显然是不变的
那么就可以钦定\(u\)的颜色为0,对于任意一种边的染色,都可以推出连通块中的其他点的颜色,因此方案数就是\(2^{N-1}\),\(N\)为连通块的点数
这样所有连通块的方案数乘起来就是对答案的贡献,即\(2^{row+lin-C}\),\(C\)为连通块数
代码如下:
T3 accept
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<bitset>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn=5e3+5;
const int mod=1e9+7;
#define int long long
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int n,m,fa[maxn<<1];
int size[maxn<<1];
char mp[maxn][maxn];
int get(int x)
{
if(x==fa[x]) return x;
return fa[x]=get(fa[x]);
}
void merge(int x,int y)
{
x=get(x); y=get(y);
if(x!=y) {fa[y]=x; size[x]+=size[y]; size[y]=1;}
return ;
}
int dn,dm;
int cnt[maxn];
int s[10],ans=1;
signed main()
{
//freopen("square.in","r",stdin);
//freopen("square.out","w",stdout);
n=read(); m=read();
for(int i=1;i<=n;i++) scanf("%s",mp[i]+1);
dn=(n>>1)+1; dm=(m>>1)+1;
if(n&1)
{
int i(0);
for(i=1;i<=m&&mp[dn][i]==mp[dn][m-i+1];i++);
if(i<=m) ans*=2;
}
if(m&1)
{
int i(0);
for(i=1;i<=n&&mp[i][dm]==mp[n-i+1][dm];i++);
if(i<=n) ans*=2;
}
for(int i=1;i<=(n>>1)+(m>>1);i++) fa[i]=i,size[i]=1;
for(int i=1;i<=(n>>1);i++)
{
for(int j=1;j<=(m>>1);j++)
{
s[1]=mp[i][j];
s[2]=mp[i][m-j+1];
s[3]=mp[n-i+1][j];
s[4]=mp[n-i+1][m-j+1];
sort(s+1,s+1+4);
int base=24;
for(int i=1;i<=4;i++) {cnt[s[i]]++; base/=cnt[s[i]];}
for(int i=1;i<=4;i++) cnt[s[i]]=0;
int len=unique(s+1,s+1+4)-s-1;
if(len==4) merge(i,(n>>1)+j),base=12;
ans=ans*base%mod;
}
}
for(int i=1;i<=(n>>1)+(m>>1);i++)
for(int j=1;j<size[i];j++) ans=ans*2%mod;
printf("%lld\n",ans);
return 0;
}
upd:解释一下染色的意义
每个行和列拆成点,这样每个点的颜色表示这个行或列是否翻转
然后,显然的是,这个二分图中的任意两点的连边的颜色(即如果\(i,j\)连边,那么这条边的颜色就是\(col_i\oplus col_j\))代表某行和某列交出来的那个点所在的组初始是能达到所有偶排列还是所有奇排列
由于我们需要统计的是所有的边的颜色情况总数,但是边是与点的颜色有关的
我们只能考虑多少种点的染色情况是可行的
那么不如直接揪出一个生成树,给这颗生成树随意染色(\(2^{N-1}\)),然后能推断出所有点的颜色
需要注意的是:所有点颜色取反对于答案没有贡献(即对于所有边,点色均取反,但是边色是不变的,这是异或的性质),所以可以直接钦定某一点点的颜色为0,从而推出所有的点的颜色,这样二分图中原有的每条边的颜色也就确定了
本文作者:Mastey,转载请注明原文链接:https://www.cnblogs.com/mastey/p/17271514.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号