3-28省选集训
前言
想哭
A. 原
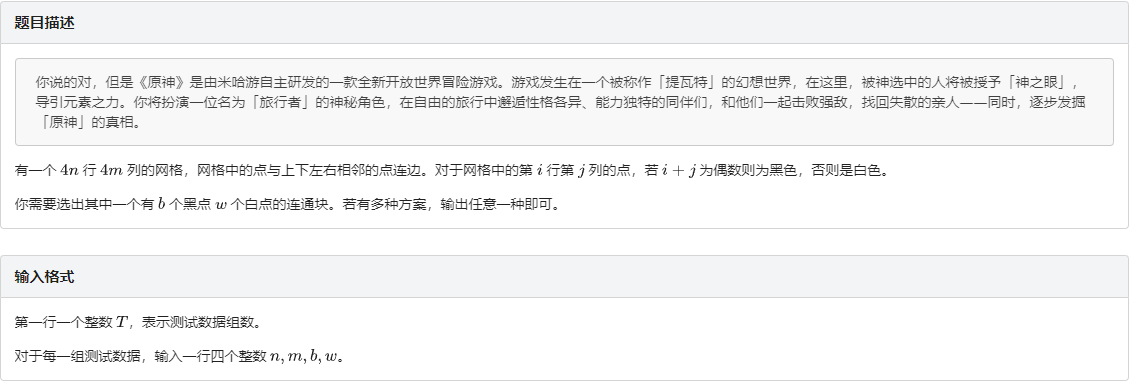


官方题解:
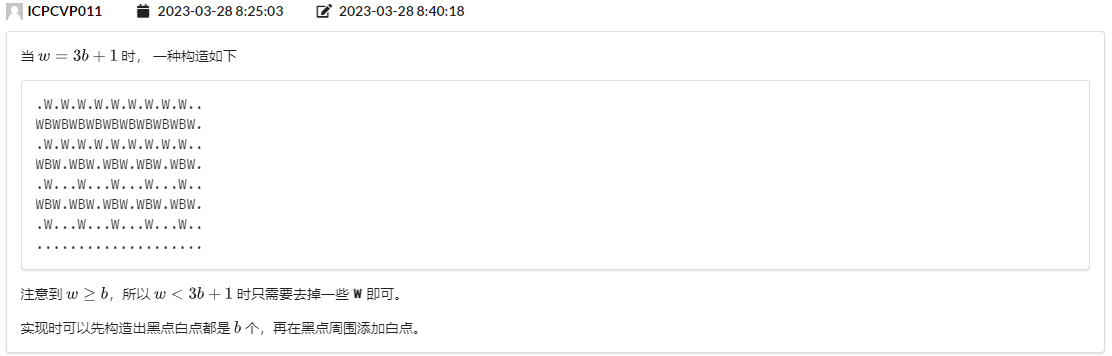
考场想偏了,首先证明\(w\leq 3b+1\)很简单,但是考场就因为这个证明想偏了
我们如果按照某一行无限延长,自然很好证
但是注意本题是有外围\(4\times n,4\times m\)限制的
所以我们不能直接构造一个很长的行,像下面这样
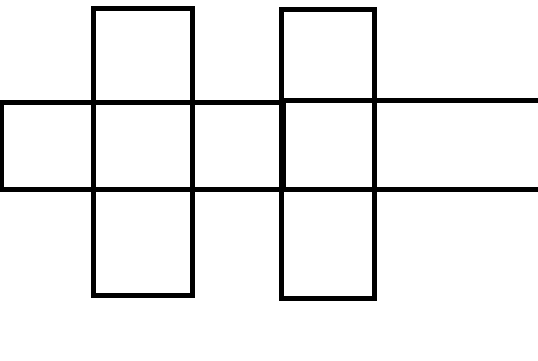
那么,考场上第二个错误思路出现了
如果我一行放不下不能甩到下一行来吗?
像这样把每一行堆满

显然不行,这样做会导致很多的\(W\)重复,导致如果\(B\)本来数量就少,这样做并不能最大化利用\(B\)
一个显然的hack数据:

如果\(W\)直接变成\(B\)的三倍左右,那么上面那种构造也就给每个\(B\)分到两个\(W\),显然无法达到要求
然后就似了
这个方法本来就是错的
考虑正解
我们应该找到一个分散的更开的,且满足如果放满可以达到\(B\times 3+1\)的方案
如下
那么我们发现,我们如果令\(W=B\),构造出一个骨架,显然\(W\geq B\)
那么在上面的\(B\)旁边添加剩余的\(W\)即可
然后发现,骨架长成这样子
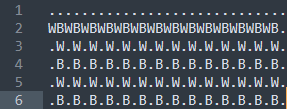
由于宽一定是偶数,我们第二行最后留出一个位置,这样就必须在\(m\times 4-2\)位置停止构造
然后可以发现,上图的构造保证当前个数满足\(W=B\)
而且把所有能填\(W\)的位置填满后,满足\(W=B\times 3+1\)
因此,本题无了
附45pts错解:
T1 45pts WA
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<bitset>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn=2e3+5;
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int T,n,m,b,w;
int dx[10]={0,0,1,-1,0,1,0,-1};
int dy[10]={-1,1,0,0,1,0,-1,0};
int mp[maxn][maxn];
void solve()
{
n=read(); m=read();
for(int i=1;i<=n*4;i++)
for(int j=1;j<=m*4;j++) mp[i][j]=0;
b=read(); w=read();
bool flag=0;
int x=2,y=2;
int tag(0);
while(b&&w&&(!flag))
{
if(w>=b+3)
{
mp[x][y]=1; b--;
for(int i=0;i<4&&b<=w;i++)
if(!mp[x+dx[i]][y+dy[i]])
mp[x+dx[i]][y+dy[i]]=1,w--;
y+=2;
}
while(b<w&&b>0&&w>0)
{
if(y>=m*4) {tag=1; break;}
mp[x][y]=1; b--;
for(int i=1;i<4&&b<w;i++)
if(!mp[x+dx[i]][y+dy[i]])
mp[x+dx[i]][y+dy[i]]=1,w--;
y+=2;
}
if(!b&&w)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(w==0) break;
if(!mp[i][j]&&(i+j)&1) for(int k=0;k<4;k++)
if(mp[i+dx[k]][j+dy[k]]) {mp[i][j]=1; break;}
w--;
}
}
break;
}
while(b==w)
{
if(!b) break;
if(y>=m*4) {tag=1; break;}
mp[x][y]=1; b--;
mp[x+dx[1]][y+dy[1]]=1; w--;
y+=2;
}
if(tag)
{
if(b==w) {x++; if((x+2)&1) y=3; else y=2;}
else x+=2,y=2;
}
}
if(!b&&w==1) mp[1][2]=1;
for(int i=1;i<=n*4;i++)
{
for(int j=1;j<=m*4;j++)
{
if(!mp[i][j]) {printf("."); continue;}
if((i+j)&1) printf("W");
else printf("B");
}
printf("\n");
}
return ;
}
int main()
{
freopen("nsdd.in","r",stdin);
freopen("nsdd.out","w",stdout);
T=read();
while(T--) solve();
return 0;
}
T1 accept
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<bitset>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn=205;
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int T,n,m,b,w;
bool mp[maxn][maxn];
bool check(int x,int y)
{return (mp[x-1][y]||mp[x+1][y]||mp[x][y-1]||mp[x][y+1]);}
void solve()
{
n=read(); m=read();
b=read(); w=read();
if(!b&&w) mp[1][2]=1;
for(int i=1;i<=m*4-2&&b;i+=2)
{mp[2][i]=mp[2][i+1]=1; b--; w--;}
for(int i=2;i<=m*4-1&&b;i+=4)
for(int j=3;j<=n*4-2&&b;j+=2)
{mp[j][i]=mp[j+1][i]=1; w--; b--;}
for(int i=1;i<=n*4&&w;i++)
for(int j=1;j<=m*4&&w;j++)
if((!mp[i][j])&&check(i,j)&&((i+j)&1)) {mp[i][j]=1; w--;}
for(int i=1;i<=n*4;i++)
{
for(int j=1;j<=m*4;j++)
{
if(!mp[i][j]) {printf("."); continue;}
if((i+j)&1) printf("W");
else printf("B");
}
printf("\n");
}
for(int i=1;i<=n*4;i++)
for(int j=1;j<=m*4;j++) mp[i][j]=0;
return ;
}
int main()
{
//freopen("nsdd.in","r",stdin);
//freopen("nsdd.out","w",stdout);
T=read();
while(T--) solve();
return 0;
}
B. 神
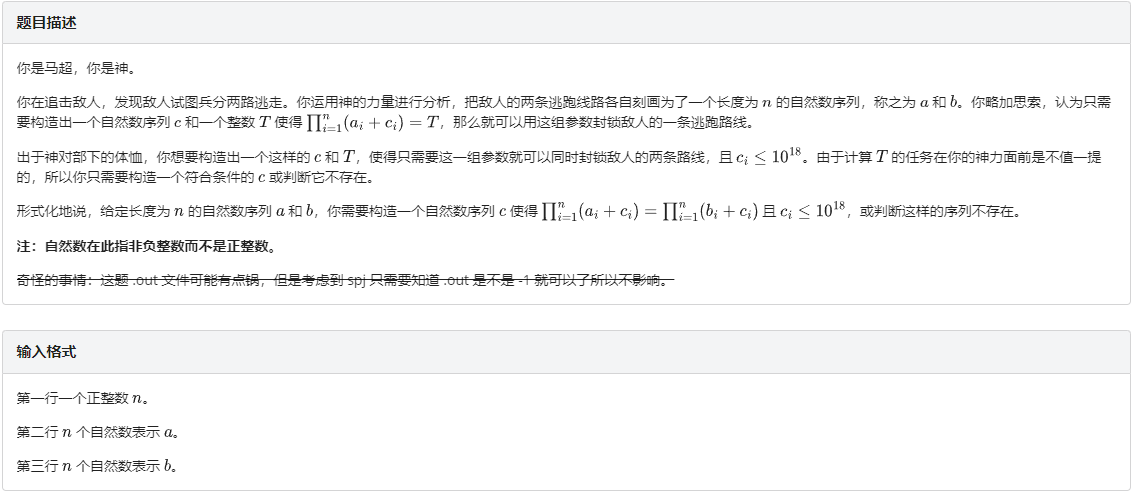
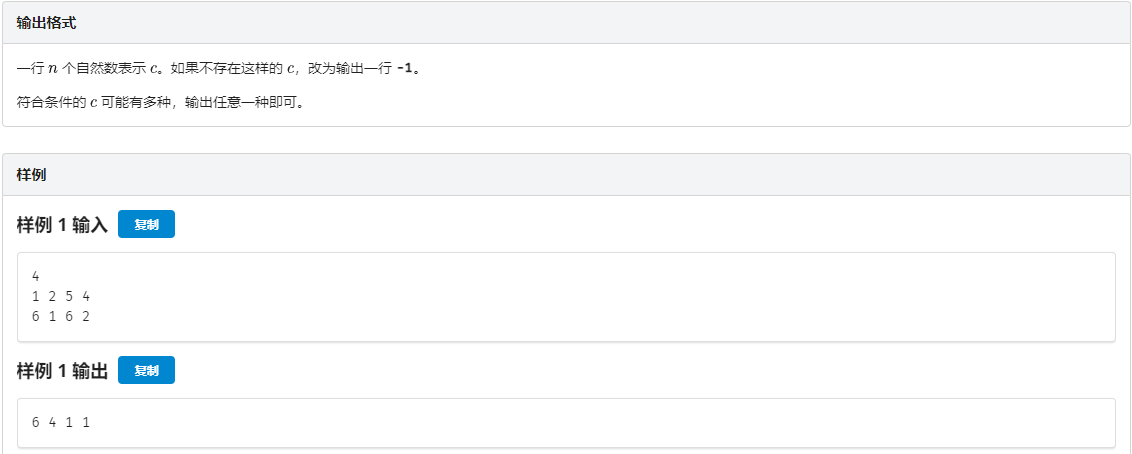

官方题解:

讲一种结合题解和lx做法的解法
首先我们发现,像题解一样,两个同样是\(a_i>b_i\)的\(i\)是可以合并的
我们假设\(a_1>b_1\),\(a_2>b_2\)
我们设\(a_1-b_1=d_1\),\(a_2-b_2=d_1\)
\(a_1=b_1+d_1,a_2=b_2+d_2\)
我们如果想使变化后的值\(a_1=b_2\),这样就能在乘积等式中约掉这两项,化简问题,即令\(a_1+c_1=b_2+c_2\)
然后\(b_1+c_1=a_1+c_1-d_1=b_2+c_2-d_1=a_2-d_2+c_2-d_1\)
移项:\(b_1+c_1+d_1+d_2=a_2+c_2\)
我们设\(b_1+c_1\)为新的\(b'_1\)
同理\(a_2+c_2\)为新的\(a'_2\)
那么相当于出现了一个新的两项,且\(a'_2>b'_1\),\(a'_2=b'_1+(d_1+d_2)\),差变为了两个元素差之和
注意!这里的\(c_1,c_2\)并不是最终答案,最终答案可能是\(c_1+q,c_2+q\),\(q\)为常数,这里只是为了取到\(a'_1=b'_2\)而取的\(c_1,c_2\)
然后我们发现,这个\(a'_2,b'_1\)组成了新的二元组,两个缩成一个了
然后可能会有疑问,如果我们继续在\((a'_2,b'_1)\)上加某个数\(x\)变成\((a_2+c_2+x,b_1+c_1+x)\),那么原来的\(b_2\)和\(a_1\)也要加上,变成\(b_2+c_2+x\)和\(a_1+c_1\)
我们发现等式两边还是成立,即\(b_2+c_2+x=a_1+c_1+x\)
说明仍满足条件,\(a'_2,b'_1\)可以作为一个二元组正常使用(同时加某个数)
可以发现:这样每个二元组的最大值\(-\)这个最大值原先的值即为那个原先位置的答案
这样不光\(a_i>b_i\),\(a_i<b_i\) 也是可以缩成一个二元组,这里不多赘述
问题转化为:存在\(a_1<b_1,a_2>b_2\)
怎么使\((a_1+a)\times (a_2+b)=(b_1+a)\times (b_2+b)\)
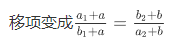

我们发现,这样就找出来答案了,我们考虑一步步倒推回去
由于我们给最后的\(a_2,b_1\)赋值为1e18,\(b_1\)最终变成了\(b'_1=b_1-(f-k\times d_1)\),\(a_2\)变成了\(a'_2=a_2-(f-k\times d_2)\),发现这两个都是原来位置二元组中较大的值,那么这两个数原来的位置答案就是\(a'_2-a_i,b'_1-b_j\),\(i,j\)就是原来的下标
我们倒着找到每个位置的最大值变成了多少就行
由于我们倒推的过程就是把二元组拆开
模拟这个过程
觉得统计答案这点 有点难表达,大概感觉就是从后往前一个一个合并,然后再倒着求每个位置最大值要变成多少
其实就是减去当前下标\(i\)的\(d_i\)
\(k\)值的选取注意让答案别变成负数即可
T2 accept
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<bitset>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn=1e6+5;
const ll f=1e18;
#define int long long
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int n;
int a[maxn],b[maxn];
int d[2],vec[maxn];
int flaga=0,flagb(0),flag(0);
void deal_full()
{
for(int opt=0;opt<=1;opt++)
{
int tmp=1e18,sum(0);
for(int i=1;i<=n;i++)
{
if(a[i]==b[i]) continue;
if((a[i]<b[i])!=opt) continue;
vec[i]=tmp;
tmp-=abs(a[i]-b[i]);
sum+=abs(a[i]-b[i]);
}
d[opt]=sum;
}
int k=100;
for(int i=1;i<=n;i++)
{
if(a[i]==b[i]) vec[i]=a[i];
else if(a[i]>b[i]) vec[i]-=f-d[0]*k;
else vec[i]-=f-d[1]*k;
}
for(int i=1;i<=n;i++)
printf("%lld ",vec[i]-max(a[i],b[i]));
return ;
}
signed main()
{
//freopen("god.in","r",stdin);
//freopen("god.out","w",stdout);
n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++) b[i]=read();
for(int i=1;i<=n;i++)
if(a[i]>b[i]) flaga++;
else if(a[i]<b[i]) flagb++;
else flag++;
if(flag==n)
{
for(int i=1;i<=n;i++) printf("%d ",0);
printf("\n");
return 0;
}
else if(flaga==n||flagb==n) printf("-1\n");
else deal_full();
return 0;
}
本文作者:Mastey,转载请注明原文链接:https://www.cnblogs.com/mastey/p/17264980.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号