3-27省选集训
前言
寄
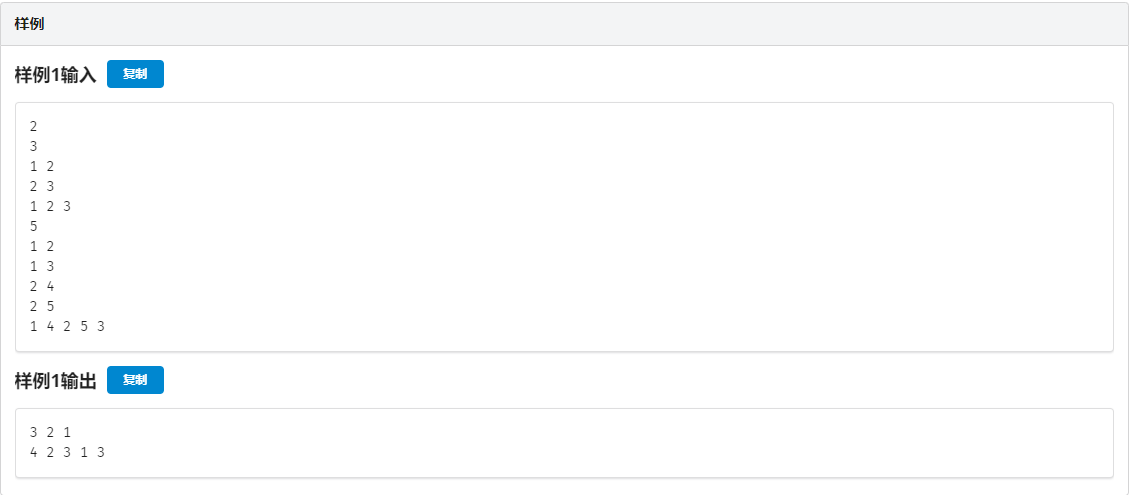
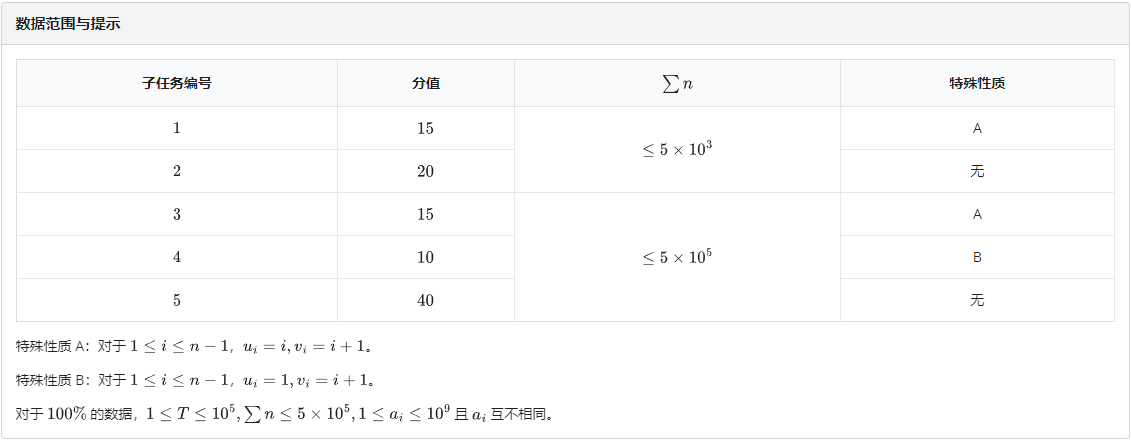
A. 理塘之王
官方题解:

考场上推了个性质:以每个点为根的答案即该点子树中到根路径上的点的值均\(\leq\)该点值的点个数
考虑证明: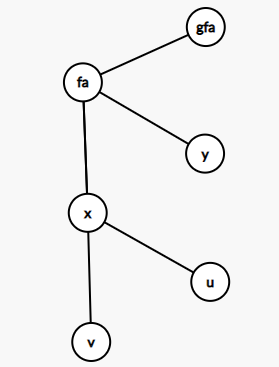
假设当前有个点 \(z\) 在 \(gfa\) 外部
如果\(val[gfa]>val[v]>val[u]>val[fa]\)
说明正常从\(z\)无法直接到达\(u,v\)
那么可能会有疑问,如果\(z\)能到达\(y\),再从\(y\)中转即可
那么需要满足\(val[y]>val[gfa]\),那如果再从\(y\)到\(u,v\)
显然不满足\(val[y]<val[u/v]\)
因此\(u,v\)是无法被访问的,不会产生贡献
然后可以发现,剩下的我们按照每次走能走的点里面尽可能小的
就可以全部走一遍
答案即抛出无法访问的点,剩下的点的个数
结合部分分可以拿到60
考场上一直在想这个问题能不能优化,然后想了一下主席树线段树合并之类的
觉得实现特别麻烦,而且貌似带修
考场还挂了15(嘤嘤嘤
T1 60pts
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<bitset>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn=5e5+5;
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int T,n;
struct edge
{
int to,next,c;
}g[maxn<<2];
int head[maxn],cnt(0);
inline void add(int a,int b)
{
g[++cnt].to=b;
g[cnt].next=head[a];
head[a]=cnt;
return ;
}
int top[maxn],son[maxn],fa[maxn];
int dep[maxn],size[maxn];
int seg[maxn],rev[maxn],t(0);
void dfs(int u,int f)
{
size[u]=1; fa[u]=f;
dep[u]=dep[f]+1;
for(int i=head[u];i;i=g[i].next)
{
int v=g[i].to;
if(v==f) continue;
dfs(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
return ;
}
void dfs2(int u,int p)
{
top[u]=p;
seg[u]=++t; rev[t]=u;
if(son[u]) dfs2(son[u],p);
for(int i=head[u];i;i=g[i].next)
{
int v=g[i].to;
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
return ;
}
int val[maxn];
int f[maxn][25],Log[maxn];
int query(int l,int r)
{
int k=Log[r-l+1];
return max(f[l][k],f[r-(1<<k)+1][k]);
}
int ask(int x,int y)
{
int ret=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ret=max(ret,query(seg[top[x]],seg[x]));
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ret=max(ret,query(seg[x],seg[y]));
return ret;
}
int root(0);
int b[maxn],ans(0);
void dfs3(int u,int f)
{
if(ask(root,u)<=val[u]) ans++;
for(int i=head[u];i;i=g[i].next)
{
int v=g[i].to;
if(v==f) continue;
dfs3(v,u);
}
return ;
}
void deal_30()
{
for(int i=1;i<=n;i++)
{ans=0; root=i; dfs3(i,0); printf("%d ",ans);}
printf("\n");
return ;
}
int st[maxn],tail(0);
int lef[maxn],rig[maxn],sum[maxn];
void deal_15()
{
tail=0;
for(int i=1;i<=n;i++)
{
while(tail&&val[i]>val[st[tail]])
{rig[st[tail]]=i; tail--;}
st[++tail]=i;
}
for(int i=1;i<=n;i++)
if(!rig[i]) rig[i]=n+1;
tail=0;
for(int i=n;i>=1;i--)
{
while(tail&&val[i]>val[st[tail]])
{lef[st[tail]]=i; tail--;}
st[++tail]=i;
}
for(int i=1;i<=n;i++)
{sum[lef[i]+1]++; sum[rig[i]]--;}
for(int i=1;i<=n;i++) sum[i]+=sum[i-1];
for(int i=1;i<=n;i++)
printf("%d ",sum[i]);
printf("\n");
return ;
}
int is[maxn],vec[maxn];
void deal_10()
{
for(int i=1;i<=n;i++) is[i]=0;
int tot(0);
for(int i=1;i<=n;i++)
if(ask(1,i)<=val[i]) is[i]=1,tot++;
printf("%d ",tot);
vec[0]=0;
for(int i=1;i<=n;i++)
if(is[i]) vec[++vec[0]]=val[i];
sort(vec+1,vec+1+vec[0]);
for(int i=2;i<=n;i++)
{
int pos=lower_bound(vec+1,vec+1+vec[0],val[i])-vec;
printf("%d ",tot-is[i]+1-(pos-1));
}
printf("\n");
}
int main()
{
freopen("ltc.in","r",stdin);
freopen("ltc.out","w",stdout);
T=read();
Log[0]=-1;
for(int i=1;i<=5e5;i++) Log[i]=Log[i>>1]+1;
while(T--)
{
n=read();
cnt=0; t=0;
for(int i=1;i<=n;i++) head[i]=0;
for(int i=1;i<=n;i++)
{
son[i]=top[i]=dep[i]=0;
fa[i]=seg[i]=rev[i]=0;
f[i][0]=0; lef[i]=rig[i]=0; sum[i]=0;
}
bool flag=1;
for(int i=1;i<n;i++)
{
int u,v;
u=read(); v=read();
if(v!=u+1) flag=0;
add(u,v); add(v,u);
}
dfs(1,0); dfs2(1,1);
for(int i=1;i<=n;i++) b[i]=val[i]=read();
sort(b+1,b+1+n);
for(int i=1;i<=n;i++)
val[i]=lower_bound(b+1,b+1+n,val[i])-b;
for(int i=1;i<=n;i++) f[i][0]=val[rev[i]];
for(int j=1;(1<<j)<=n;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);
if(flag) deal_15();
else if(n<=5000) deal_30();
else deal_10();
}
return 0;
}
然后我们考虑正解,题解写的很清楚了,实现只要倒着做很简单
然后我就在想这两个性质有没有相似性
然后发现我一开始的想法里面有一句话:走能走的里面最小的
对应了题解里当前最大值向连通块里面最大值连边,这样可以每次尽可能少的缩小最大值
感觉还是思维狭隘了
应该用处理最短路加边的那种思想来搞
不多说了
T1 accept
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<bitset>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn=5e5+5;
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int T,n;
vector<int> g[maxn],g2[maxn];
int fa[maxn],id[maxn];
int val[maxn],dep[maxn];
bool cmp(int a,int b) {return val[a]<val[b];}
int find(int x)
{
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
g2[x].push_back(find(y));
fa[find(y)]=x;
return ;
}
void dfs(int u,int p)
{
dep[u]=dep[p]+1;
for(int v:g2[u]) dfs(v,u);
return ;
}
void solve()
{
n=read();
for(int i=1;i<=n;i++)
g[i].clear(),g2[i].clear(),fa[i]=id[i]=i;
for(int i=1;i<n;i++)
{
int u,v;
u=read(); v=read();
g[u].push_back(v);
g[v].push_back(u);
}
for(int i=1;i<=n;i++) val[i]=read();
sort(id+1,id+1+n,cmp);
for(int i=1;i<=n;i++)
{
int u=id[i];
for(int v:g[u]) if(val[v]<val[u]) merge(u,v);
}
dfs(id[n],0);
for(int i=1;i<=n;i++) printf("%d ",dep[i]);
printf("\n");
return ;
}
int main()
{
//freopen("ltc.in","r",stdin);
//freopen("ltc.out","w",stdout);
T=read();
while(T--) solve();
return 0;
}
B. 测你们码
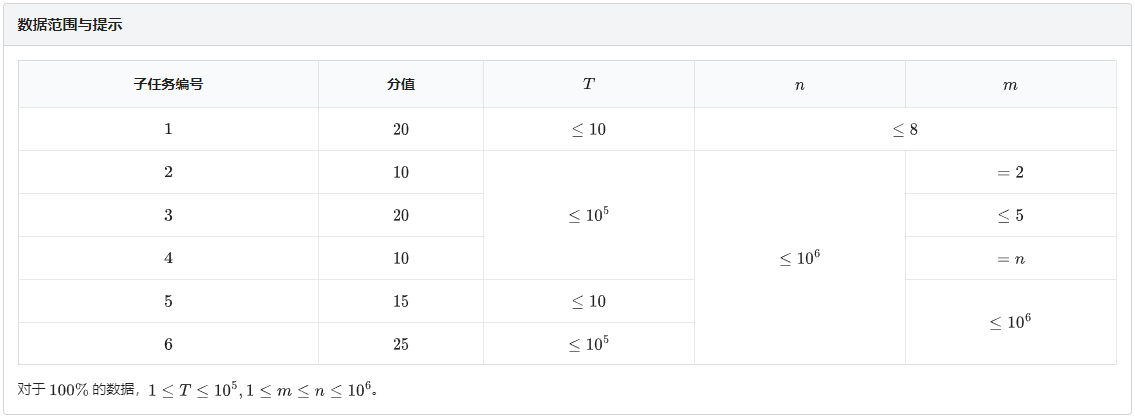
官方题解:

几个要点说一下:
首先,题解里在一个排列里面的答案是\((n-m+1)m!(n-m)!\)
我们可以这样理解,相当于我们在\(n\)长度的区间里面任取开头,然后添入连续的\(m\)长度的排列,剩下的部分填\(n-m\)个数构成\(n\)长度排列
其次,关于这个的理解需要说一下

首先我们看图
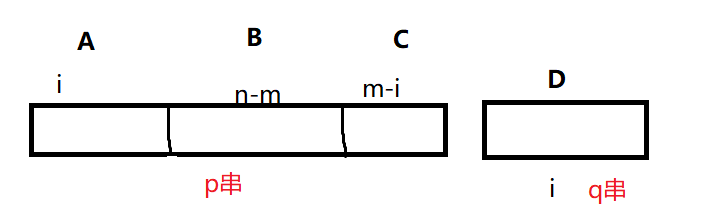
我们想要把CD拼成长为\(m\)的排列
我们现在假设C中元素已经是\(\leq m\)的了
想要证明此时A中元素也必定\(\leq m\),从而证明A+C是\(m\)的某个排列
然后证明A=D,就可以证明A+D也为\(m\)的某个排列
我们发现,假设如果A里面有个位置\(j\),\(j\)上的数是大于\(m\)的
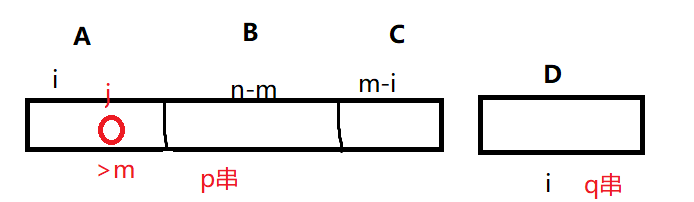
那么按照下面这样的方法,我们可以构造出下一个\(n\)长度排列

容易发现,想要A+C为\(m\)的某个排列,需要里面的数都\(<m\),我们想要D中的数\(<m\),这样必须把\(j\)换成一个\(\leq m\)的数
由于现在C中的数都是\(\leq m\)的,那么我们只能从B中通过排序找到一个\(\leq m\)的数来替换\(j\),此时需要单调递减的区间为\([j+1,n]\),如下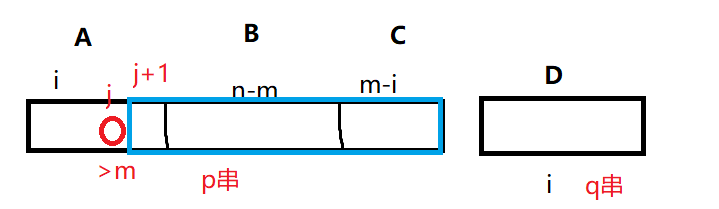
由于我们找的是\([j+1,n]\)里面第一个大于\(j\)位置上数的数,那么交换之后,\(j\)位置上的数只能更大
想要令其\(\leq m\)只能考虑排序,那么比\(j\)位置上的数大的数只能是\([j+1,n]\)里面最大的数
由于\([j+1,n]\)是单调递减的,那么排序后一定保证\([j+1,i]\)里面存在C中的数
这样调整之后,得到的即为D
那么C和D就会有公共的数,就不会构成排列了
因此矛盾
证明A里面必须是\(\leq m\)的
然后考虑我们需要A=D
只有一种特殊情况需要考虑: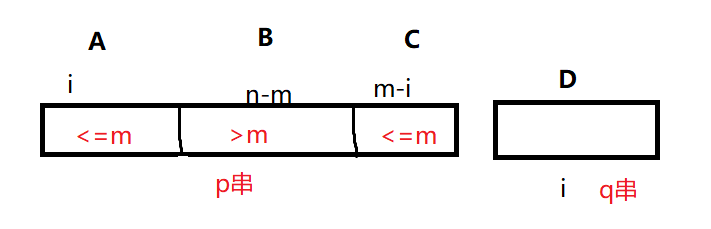
由于B中元素都是\(>m\)的,不会存在A中某个位置\(j\),\(j<i\),然后\([j,n]\)构成递减序列的,唯一一种情况就是\(j=i\)时,如果B+C恰好构成了单调递减的情况
会导致把\(j\)位置上的数换出去,这样得到的前\(i\)个数就不是原来的前\(i\)个数了,第\(i\)个数会出现不同
那么,只有B+C构成单调递减时,D\(\neq\)A
那么,这样D\(\neq\)A的方案即为,选出\(i\)个数作为A,可以随便排列,剩下的数从大到小放进B和C中
方案数\(C_m^i\times i!\),题解中的写法算出来也是一样的
然后统计就简单了
本文作者:Mastey,转载请注明原文链接:https://www.cnblogs.com/mastey/p/17261483.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号