归并排序分析

归并排序：

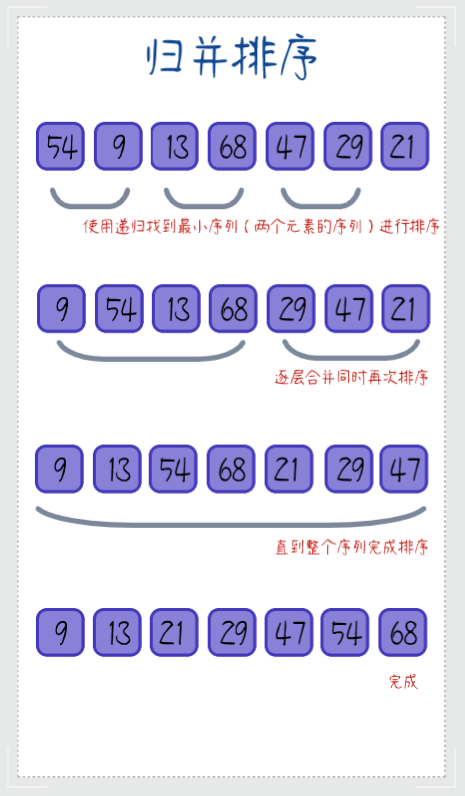
归并排序思路是使用分治策略，递归将一组序列划分成若干小序列进行排序，再将小序列重新结合得到这组序列的顺序。

图示思路

代码

typedef int ElemType;

void Msort(ElemType A[], ElemType TmpArray[], int Left, int Right)
//递归分成若干小序列
{
    int Center;
    if (Left < Right)
    {
        Center = (Left + Right) / 2;
        Msort(A, TmpArray, Left, Center);
        Msort(A, TmpArray, Center + 1, Right);
        Merge(A, TmpArray, Left, Center + 1, Right);
    }
}

void Mergesort(ElemType a[], int n)
{
    ElemType *TmpArray;
    TmpArray = malloc(n * sizeof(ElemType));
    if (TmpArray != NULL)
    {
        Msort(a, TmpArray, 0, n - 1);
        free(TmpArray);
    }
}

void Merge(ElemType A[], ElemType TmpArray[], int Lpos, int Rpos, int RightEnd)
//将两组较小序列重新结合成较大的有序序列
{
    int i, LeftEnd, NumElemts, TmpPos;

    LeftEnd = Rpos - 1;
    TmpPos = Lpos;
    NumElemts = RightEnd - Lpos + 1;

    while (Lpos <= LeftEnd && Rpos <= RightEnd)
        if (A[Lpos] <= A[Rpos])
            TmpArray[TmpPos++] = A[Lpos++];
        else
            TmpArray[TmpPos++] = A[Rpos++];
    while (Lpos <= LeftEnd)
        TmpArray[TmpPos++] = A[Lpos++];
    while (Rpos <= RightEnd)
        TmpArray[TmpPos++] = A[Rpos++];

    for (i = 0; i < NumElemts; i++, RightEnd--)
        A[RightEnd] = TmpArray[RightEnd];
    
}

传统的归并排序（后期可能会谈到TimSort）的时间复杂度没有好坏之分，都是O(n*log2n)，且而所使用的比较次数几乎是最优的，他是递归算法一个很好的实例。在归并排序中，相等的元素的顺序不会改变，所以它是稳定的算法。

但他很难用于主存排序，主要问题在于合并两个排序的表需要线性附加内存，在整个算法中还要花费将数据拷贝的临时数组再拷贝回来这样一些附加工作。这种拷贝可以通过在机柜交替层次时审慎地钻换A和TmpArray的角色来得到避免。

（文章摘录《数据结构与算法分析C语言描述》机械工业出版社）