AcWing 798.差分矩阵

题目链接：https://www.acwing.com/problem/content/800/

 

关于二维差分

若要将二维数组中的某一个矩阵的每个元素的值加上 c，我们可以通过二维差分以达到 O(1) 的时间复杂度。

原数组：a[i][j]　　

构造差分数组：b[i][j]

也就是说：a数组是b数组的前缀和数组，b数组是a数组的差分数组。

使得a数组中 a[i][j] 是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。

 

如何构造差分数组？

和一维差分一样，我们对b数组中的 b[i][j] 修改后会影响a数组中从 a[i][j] 开始往后的每一个数，而我们只需要对指定矩阵中的元素进行修改。

类比一维差分我们可以这样操作：

b[x1][y1]+=c;
b[x1][y2+1]-=c;
b[x2+1][y1]-=c;
b[x2+1][y2+1]+=c;

对b数组进行处理，即对a数组中(x1,y1)到(x2,y2)之间的元素+c，等价于：

for(int i=x1; i<=x2; i++)
  for(int j=y1; j<=y2; j++)
    a[i][j]+=c;

理解如图：

 

 

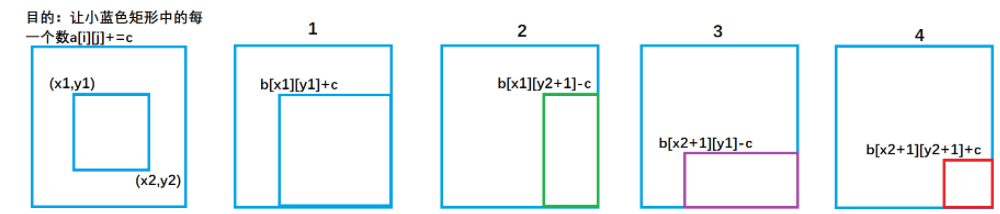
最后计算二维前缀和并输出：

求 a[i][j] 即求 b[i][j] 的前缀和，b[i][j] + = b[i][j-1] + b[i-1][j] - b[i-1][j-1]。

（当我们要计算 b[i][j] 时，在b数组中 b[i][j] 之前的元素值已经成为此点的前缀和）

---

 

放AC代码

#include<bits/stdc++.h>
using namespace std;
int a[1005][1005],b[1005][1005];//a前缀和数组，b差分数组
int n,m,q;

void insert(int x1,int y1,int x2,int y2,int c)
{//对b数组进行处理，即对a数组中(x1,y1)到(x2,y2)之间的元素+c
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}

int main()
{
    cin>>n>>m>>q;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            cin>>a[i][j];
    //构造差分数组
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            insert(i,j,i,j,a[i][j]);
    //对原数组进行操作
    while(q--)
    {
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);
    }
    //计算二维前缀和
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            b[i][j]+=b[i][j-1]+b[i-1][j]-b[i-1][j-1];
    //输出前缀和，即现在的s数组
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            cout<<b[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}