从小到大获取整数的所有因数

一种朴素的Rust语言的算法如下：

fn get_all_factors_normal(n: u64) -> Vec<u64> {
    let n_sqrt = (n as f64).sqrt().floor() as u64;
    let mut res = Vec::new();
    for i in 1..=n_sqrt {
        if n % i == 0 {
            //println!("{}", i);
            res.push(i);
            if i * i != n {
                res.push(n / i); //为了便于对比，没有把这个数插入到对应的位置，而是直接使用时间复杂度为O(1)的push
                //println!("{}", n / i);
            }
        }
    }
    res
}

这种算法时间复杂度为 \(O(\sqrt n)\)

如果能够先获得所有质因数及其数量，在B树中插入1，然后每次弹出B树的最小值，与所有可能的因数相乘，再插入B树中自动排序，那么也就能获得所有因数，代码如下：

fn get_all_factors(mut n: u64) -> Vec<u64> {
    use std::collections::BTreeMap;
    let n_sqrt = (n as f64).sqrt().floor() as u64;
    let mut vp: Vec<(u64, u32)> = Vec::new();
    for k in 2..=n_sqrt {
        if k > n {
            break;
        }
        while n % k == 0 {
            n /= k;
            if let Some(b) = vp.last_mut() {
                if b.0 == k {
                    *b = (b.0, b.1 + 1);
                } else {
                    vp.push((k, 1));
                }
            } else {
                vp.push((k, 1));
            }
        }
    }
    if n != 1 {
        vp.push((n, 1));
    }
    let empty = vec![0; vp.len()];
    let mut tr: BTreeMap<u64, Vec<u32>> = BTreeMap::new();
    tr.insert(1, empty);
    let mut res = Vec::new();
    while let Some((b, v)) = tr.pop_first() {
        //println!("{}", b);
        res.push(b);
        for (i, p) in vp.iter().enumerate() {
            if v[i] < p.1 {
                let mut new_v = v.clone();
                new_v[i] += 1;
                tr.insert(b * p.0, new_v);
            }
        }
    }
    res
}

获取所有质因数的算法的最好时间复杂度为\(O(\log(n))\) , 当\(n\)为质数时为最坏情况，时间复杂度为\(O(\sqrt n)\).

BTreeMap为B树，查找、插入、删除的时间复杂度都是\(O(\log(n))\)。为什么不用二叉堆，是因为Rust的BinaryHeap允许push重复的内容，导致产生很多重复的因数，使结果错误。

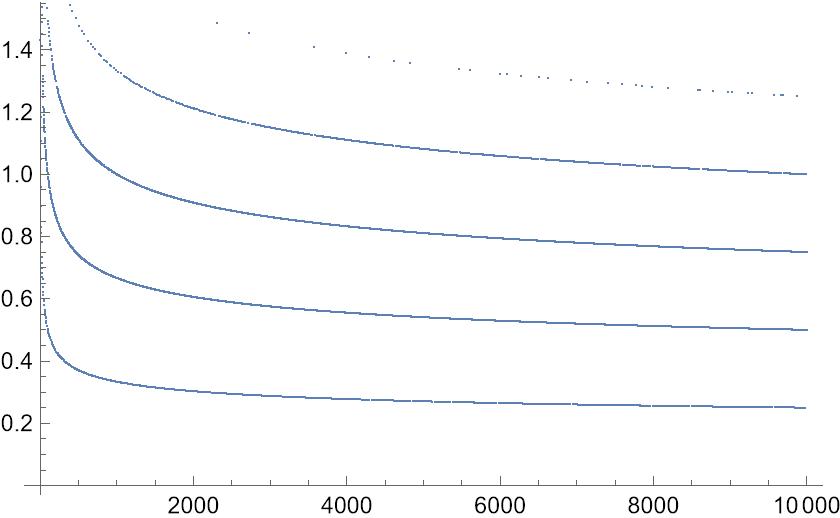
一个数的质因数数量平均有多少个？我用Mathematica粗略算了一下，就当做数量与\(\log(n)\) 成正比吧。以下是Mathematica代码及其结果：

ListPlot[Table[{n, Length[FactorInteger[n]]/Log10[n]}, {n, 2, 10000}]]

最好情况下：

获取所有质因数的算法的时间复杂度为\(O(\log(n))\) ，读取B树第一个值为\(O(\log(n))\)，每次读取后，需乘所有可能的质因数（数量约为\(\log(n)\)）并加入到B树。那么一共要读取多少次B树的第一个值呢？一个数的因数有多少个，就要读取多少次。一个数的因数的数量级为\(O(n^{\frac{1}{3}})\)。所以时间复杂度粗略估计为\(O(n^{\frac{1}{3}}\log(n)^{2})\)。

最坏情况下：

n为质数，时间复杂度为\(O(\sqrt n)\). 无需读取B树的值。

因此可得该算法的总的时间复杂度，最好情况为\(O(n^{\frac{1}{3}}\log(n)^{2})\)，最坏情况为\(O(\sqrt n)\)

对两个算法进行测试，使用cargo run --release测试代码如下：

fn main() {
    use rand::Rng;
    use std::time::Instant;
    use std::time::Duration;
    let mut rng = rand::thread_rng();
    let test_time = 100;
    let test_num: Vec<u64> = (0..test_time).map(|_| rng.gen::<u64>()).collect();
    //println!("{:?}", test_num);
    let mut time1 = Duration::new(0, 0);
    let mut time2 = Duration::new(0, 0);
    for &i in test_num.iter() {
        println!("{}", i);
        let start_time1 = Instant::now();
        let r1 = get_all_factors(i);
        let end_time1 = Instant::now();
        let t1 = end_time1 - start_time1;
        println!("Time_me : {:?}", t1);
        let start_time2 = Instant::now();
        let r2 = get_all_factors_normal(i);
        let end_time2 = Instant::now();
        let t2 = end_time2 - start_time2;
        println!("Time_nor: {:?}", t2);
        println!("Result_me :{:?}", r1);
        println!("Result_nor:{:?}", r2);
        time1 += t1;
        time2 += t2;
        println!();
    }
    println!("\nResult: \nme :{:?} \nnor:{:?}", time1, time2);
}

最终结果：

计算随机100个u64整数的所有因数用时：

我的算法：507.7144501s
普通算法：699.5194274s

在大部分的情况下，由于对因数有很多拷贝操作，所以我的算法比普通算法慢一点点，但是如果一个数的质因数的次数非常大，比如\(2^{10}11^{5}\)，那么我的算法甚至能比普通算法快一千倍。

如果加个素数表，会更快，但作为答题肯定是消耗空间过大的。

当然，这种很容易想到的算法肯定早有人做了，只是我在网上搜索现成的代码搜不到，所以写出来放在这里，如果各位有更好的算法，可以留个链接。本文如有错误，欢迎各位指正。