矩阵链相乘问题

矩阵链相乘问题

  问题描述：考虑$n$个矩阵的乘积：$A_1{A}_2\dots A_n$，确定最优的乘法顺序（最优括号化方案），使得标量（数值）乘法次数最少。其中，$A_i$为$p_{i-1}⨯p_i$矩阵，$i=1,2,\dots ,n$。

  对于两矩阵元素相乘，结果矩阵的每一个元素，由原先两矩阵的行列对应元素相乘。因此，假设假设$A_1为m\times n$矩阵，$A_2为n\times k$矩阵,$A_1{A}_2=m\times k\times n$,这么理解一共有$m\times k$个元素，每个元素进行了$n$次乘法得到。

  例：假设$A_1为10\times 5$矩阵，$A_2为5\times 20$矩阵，$A_1为20\times 10$矩阵,则有
  $(A_1{A}_2)A_3=10\times 20\times 5+10\times 10\times 20=3000$
  $A_1(A_2{A}_3)=5\times 10\times 20+10\times 10\times 5=1500$

  对于$A_1{A}_2\dots A_n$的乘法顺序总数（$P(n)$表示乘法顺序总数）可以由以下递归公式确定：
$$P(n)=\{\begin{array}{ll}1& n=1,2\\ {\sum }_{i=1}^{n-1}P(i)P(n-i)& n>2\end{array}$$
结果称为$Catalan$数,这个序列的增长速度为$\Omega (4^n/3^{3/2})$。因此要想使用暴力搜索是不现实的。

  假设$S(1,n)$所需的最少乘法次数我们有可以得到
$$S(1,n)=\underset{1\le i<n}{\min }(S(1,i)+S(i+1,n)+p_1{p}_n{p}_i)$$
可知，这个问题符合最优子结构特征，可以由子问题的解组合得到。

  由此我们考虑如何实现这个算法，为了自顶向上的求解这个问题，我们需要知道如何更新$S[i,j]$，可得：
$$S[i,j]=\{\begin{array}{ll}0& i=j\\ \underset{i<k<j}{\min }(S(i,k)+S(k+1,j)+p_i{p}_j{p}_k)& i<j\end{array}$$
以上是最少次数的迭代公式，为了构造出最终的最优括号方案，我们用另外的$K[i,j]$记录$S[i,j]$时的$k$值。
$$K[i,j]=\{\begin{array}{ll}0& i=j\\ \arg \{k:\underset{i<k<j}{\min }(S(i,k)+S(k+1,j)+p_i{p}_j{p}_k)\}& i<j\end{array}$$
代码下载

#include <iostream>
#include <vector>
#include <string>
using namespace std;

//构造最优解 
void ConstructBestAnswer(const vector<vector<int>> &k,int i,int j,string &str){
    if(i>j) return;
    if(i==j) str+=("A"+to_string(i));
    else
    {
        // cout<<i<<","<<j<<endl;
        str+="(";
        ConstructBestAnswer(k,i,k[i][j],str);
        ConstructBestAnswer(k,k[i][j]+1,j,str);
        str+=")";
    }
}

string MatrixChainMultiplication(const vector<int> &MC){
    if(MC.size()<=2) return "输入不正确";
    int n = MC.size()-1;
    //初始化两个二维数组
    vector<vector<int>> S(n,vector<int>(n,0)),K(n,vector<int>(n,0));
    for (int j = 0;j < n; j++)
    {
         
        //更新S[i][j]，其中i<=j
        for (int i = j; i >= 0; i--)
        {
            if(i==j) {K[i][j] = i;continue;}
            //设置起始的S[i][j],K[i][j]
            S[i][j] = S[i][i]+S[i+1][j] + MC[i]*MC[i+1]*MC[j+1];
            K[i][j] = i;
            //因为已经计算过从i开始的顺序，所以以下从i+1开始
            for (int k = i+1; k < j; k++)
            {
                int tmp = S[i][k] + S[k+1][j] + MC[i]*MC[j+1]*MC[k+1];
                if(S[i][j]>tmp){
                    S[i][j] = tmp;
                    K[i][j] = k;
                }
            }
            
        }
        
    }

    // for (size_t i = 0; i < n; i++)
    // {
    //     for (size_t j = 0; j < n; j++)
    //     {
    //         cout<<S[i][j]<<",";
    //     }
    //     cout<<endl;
    // }
    // for (size_t i = 0; i < n; i++)
    // {
    //     for (size_t j = 0; j < n; j++)
    //     {
    //         if(i<=j) cout<<K[i][j]<<",";
    //     }
    //     cout<<endl;
    // }
    cout<<"最优解："<<S[0][n-1]<<endl;
    string ans;
    ConstructBestAnswer(K,0,n-1,ans);
    return ans;
    
}


int main(){
    //算法导论上的案例
    vector<int> input = {30,35,15,5,10,20,25};
    cout<<MatrixChainMultiplication(input)<<endl;
    system("pause");
    return 0;
}

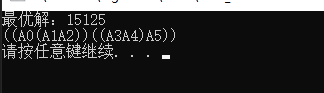
运行截图;

Reference

《算法导论》第十五章