CF1967C：Fenwick Tree 题解

CF1967C:

题意： $f(a)$ 表示 a 数列的树状数组序列，已知 $b = f(a)^k$ ，输入 k 和 b 数列，求 a 数列。

咕了好久才补的题，并不难，但是有一些启发性的知识可以分享。比赛时我发现树状数组的转移矩阵很稀疏，于是没想那么多就开始模拟矩阵乘，TLE了，后来仔细算了下发现是 $nlog^3n$ 的复杂度。

Solution：

树状数组是二叉树吗，显然不是。（但有些初学者误以为是二叉树，因为它名字叫二叉索引树）

我们画出两层树状数组来：

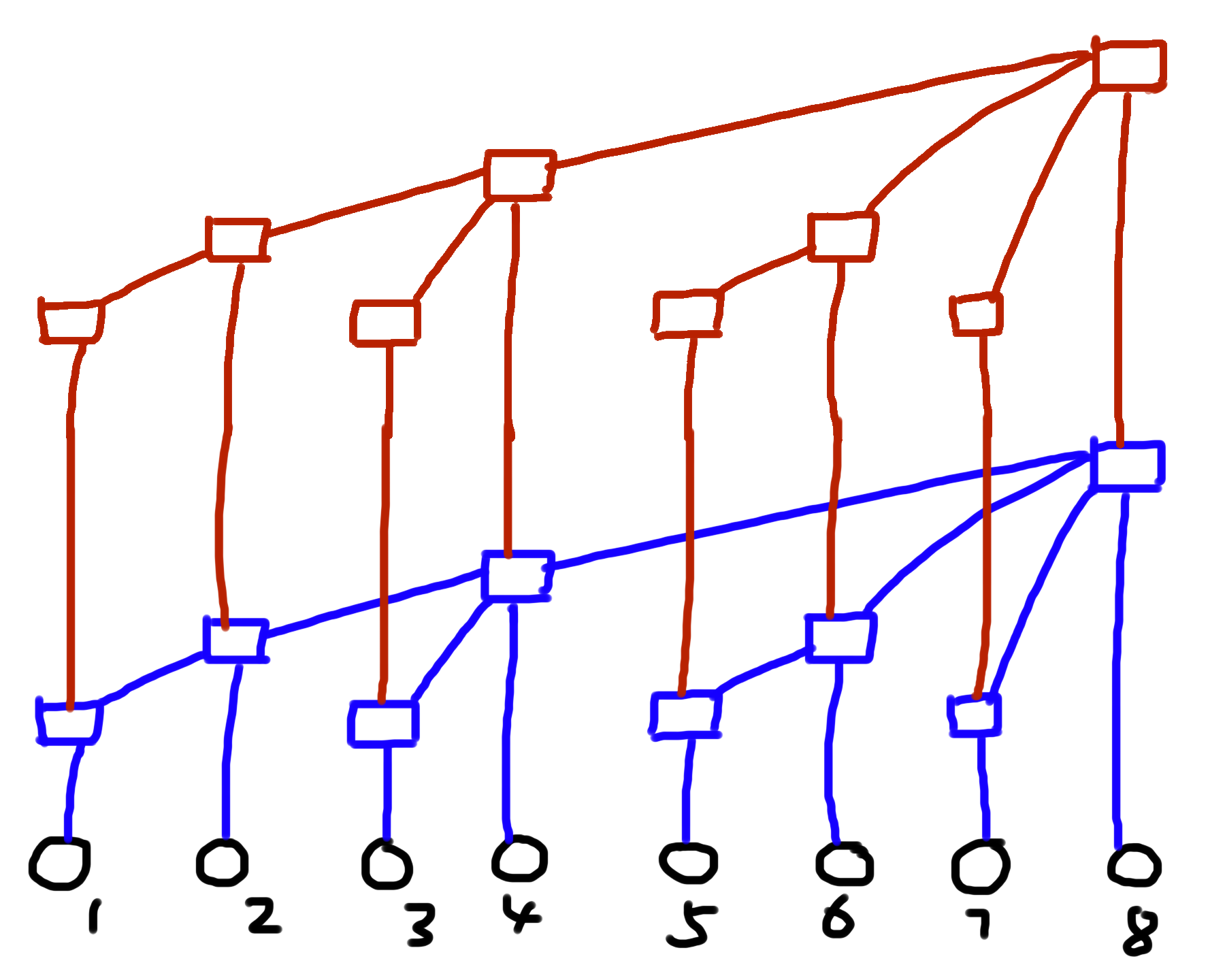
在单层树状数组中，每个方点的值维护的是儿子们的和。

反过来看，就是每个圆点的值会沿着线向祖先节点转移，并且它的值只会转移给最多 log 个祖先结点。

当单层树状数组变成了双层，我们依然可以画出这样的转移路径来，这时圆点到方点的每一条路径，都是数列 a 的贡献转移给 b 的方案。

上图中 $a[3]$ 转移到 $b[8]$ 的所有路径用绿色标出，可以看到有三条路径可以转移到 $b[8]$ ，也就是说， $b[8]$ 最终的值加了三次 $a[3]$ 。其他点也是如此，比如 $b[8]$ 加了一次 $a[8]$ ，加了两次 $a[7]$ 。

路径数量就是 a 对 b 贡献的倍率，可以用组合数来求，纵向有 K 条线，横向有 log 条线。虽然 K 很大，但是从组合数公式入手，分子分母分别只有 log 项，暴力计算即可，复杂度 nlogn。

已知 a 计算 b 容易，反过来也不难。只需要让 $b_i$ 减去 $a_1...a_{i-1}$ 对它的贡献，得出 $a_i$ 对 $b_i$ 的贡献，这个贡献只有一次，就是 $a_i$ 本身。

#include <bits/stdc++.h>
#define FOR() ll le=e[u].size();for(ll i=0;i<le;i++)
#define QWQ cout<<"QwQ\n";
#define ll long long

using namespace std;
const ll N=501010;
const ll qwq=303030;
const ll inf=0x3f3f3f3f;
const ll p=998244353;

inline ll read() {
    ll sum = 0, ff = 1; char c = getchar();
    while(c<'0' || c>'9') { if(c=='-') ff = -1; c = getchar(); }
    while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
    return sum * ff;
}

ll T;
ll n,K;
ll f[N],a[N],ni[N];

inline ll ksm(ll aa,ll bb) {
    ll sum = 1;
    while(bb) {
        if(bb&1) sum = sum * aa %p;
        bb >>= 1; aa = aa * aa %p;
    }
    return sum;
}

inline ll C(ll A,ll B) {
    ll res = ni[B];
    for(ll i=1;i<=B;i++) (res *= (A-i+1)%p) %= p;
    return res;
}

void qiu(ll h) {
    f[0] = ni[0] = 1;
    for(ll i=1;i<=h;i++) f[i] = f[i-1] * i %p;
    ni[h] = ksm(f[h], p-2);
    for(ll i=h-1;i;i--) ni[i] = ni[i+1] * (i+1) %p;
}

int main() {
    qiu(123);
    T = read();
    while(T--) {
        n = read(); K = read();
        for(ll i=1;i<=n;i++) a[i] = read();
        for(ll i=1;i<=n;i++) {
            ll ju = 2;
            ll j = i+(i&-i);
            for(;j<=n;j+=(j&-j),ju++) {
                (a[j] -= a[i] * C(K+ju-2, ju-1) %p) %= p;
            }
        }
        for(int i=1;i<=n;i++) cout<<(a[i]%p+p)%p<<" \n"[i==n];
    }
    return 0;
}