面向对象设计与构造 第一单元总结

写在前面

带着一些惶恐与期待，终于迎来了学长口中“难顶”的OO课程。在暑假3次pre学习经验的加持下，我还是算比较顺利地完成了第一单元的三次作业。虽然分数并不出彩，但是这三次作业还是让我学到了很多东西，感触良多。正好借着这次机会，与大家分享一下我的思考历程。

第一单元主要围绕表达式的求导、结果的长度优化以及表达式的格式检查展开。通过“表达式-项-因子”的关系，让我们更加清晰的认识对象之间的关系，加深面向对象的思想。

下面我将分析每次作业的题目以及相关代码，展示我的实现方式。如果思路存在偏颇，请多多包涵，不吝赐教。

第一次作业

第一次作业的内容相对容易，是实现简单的多项式求导，相关的定义如下：

• 表达式 → 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
• 项 → [加减 空白项] 因子 | 项 空白项 * 空白项 因子
• 因子 → 变量因子 | 常数因子
• 变量因子 → 幂函数
• 常数因子 → 带符号的整数
• 幂函数 → x [空白项 指数]
• 指数 → ** 空白项 带符号的整数
• 带符号的整数 → [加减] 允许前导零的整数
• 允许前导零的整数 → (0|1|2|…|9)
• 空白项 →
• 空白字符 →（空格）| \t
• 加减 → + | -

(其中{}表示0个、1个或多个，[]表示0个或1个，|表示多个之中选择)

阅读完题目，我们可以清晰地看出一个表达式中存在的简单关系：表达式由项通过正负号连接构成，每一项都由单个因子或者多个因子相乘产生，因子则有常数因子与幂函数两个种类。

程序架构与实现方法

通过上述分析，我们可以比较轻松的得出需要建立的类：主类(MainClass)、表达式类(Polynomial)、项类(Item)、因子类(Factor)。

程序的UML图

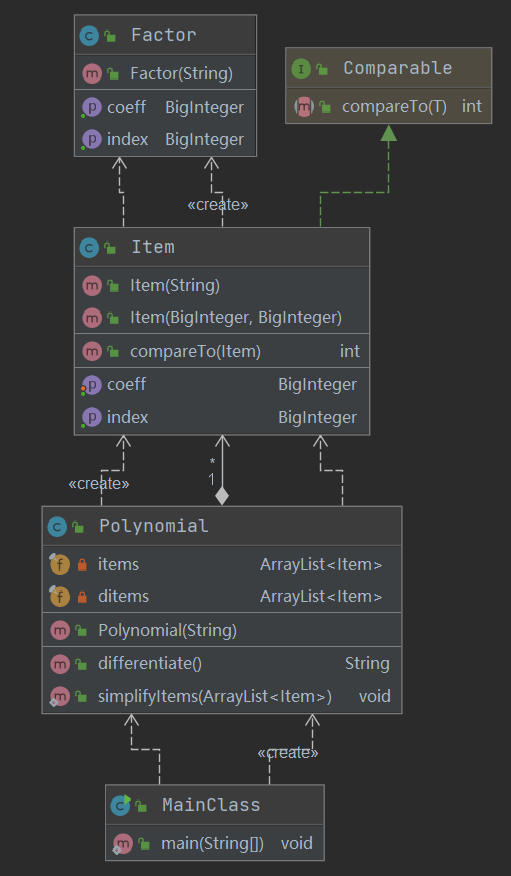
整个程序的架构还是相对简明清晰的，各个类之间的关系并不复杂，没有出现高耦合的问题。

需要注意的是，我们在建立类的时候，要兼顾后续可能存在的迭代开发。例如：幂函数的底数可以换成其他函数或者多项式，变量因子后续可能不只有幂函数存在......

笔者第一次作业建立类的时候，就缺少了这样的考虑，这直接导致了第二次作业的重构，希望读者以此为鉴。

主类(MainClass)

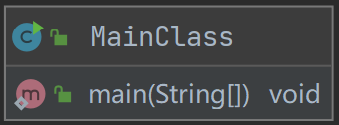
主类中不涉及字符串的处理，仅用来读入字符串并输出运算结果。

表达式类(Polynomial)

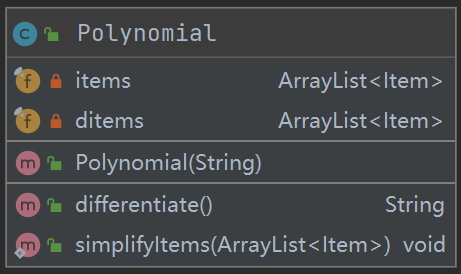
在表达式类中，我建立了两个ArrayList用来存放表达式拆出来的项以及项求导后的结果。Polynomial()方法通过正则表达式匹配项，再调用differentiate()方法对其求导。此外，新建一个simplify()方法来化简合并求导后的结果。

项类(Item)

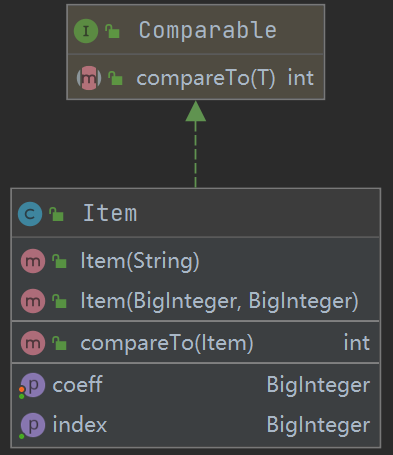
Item类继承了Comparable接口，可以通过系数进行排序，主要目的是输出求导结果时，让可能存在的正项优先输出，减少开头加负号带来的不必要的长度增加。读入每一项内容，通过正则表达式匹配拆出因子，传入因子类中。

因子类(Factor)

因子类是我这次作业比较欠缺考虑的类。因为第一次作业只有常数因子与幂函数，我就没有建立对应的常数类和幂函数类，而是直接在Factor类中进行判断、存储：

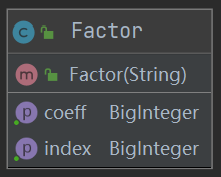
这里我通过是否含有x来判断因子的类型（这样很不好），再进行存储。存储时我做了一个简单的抽象：

Factor -> coeff * x ** index

无论常数因子还是幂函数都可以这样存储，可以选择存为一个二元对，也可以在因子类中建立coeff与index两个成员来存放。

结果化简

这次由于函数类型较少，只要别无脑toString()，对求导结果进行保存并合并，就可以得到很不错的性能分了。另外，x**2其实可以输出为x*x，这样长度又可以减少啦。

注意！！！x*x的表述在后续作业中存在风险！！！

程序结构的度量分析

类度量分析

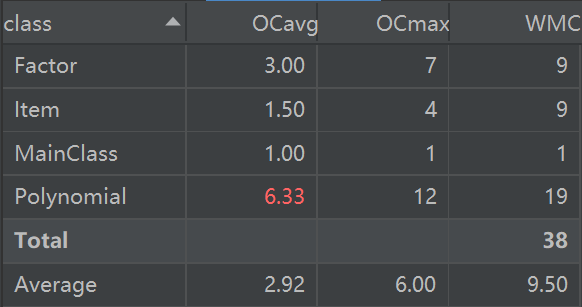
图表显示，Polynomial类的圈复杂度过高，主要原因是求导方法存在多层循环嵌套，造成性能的降低。

方法度量分析

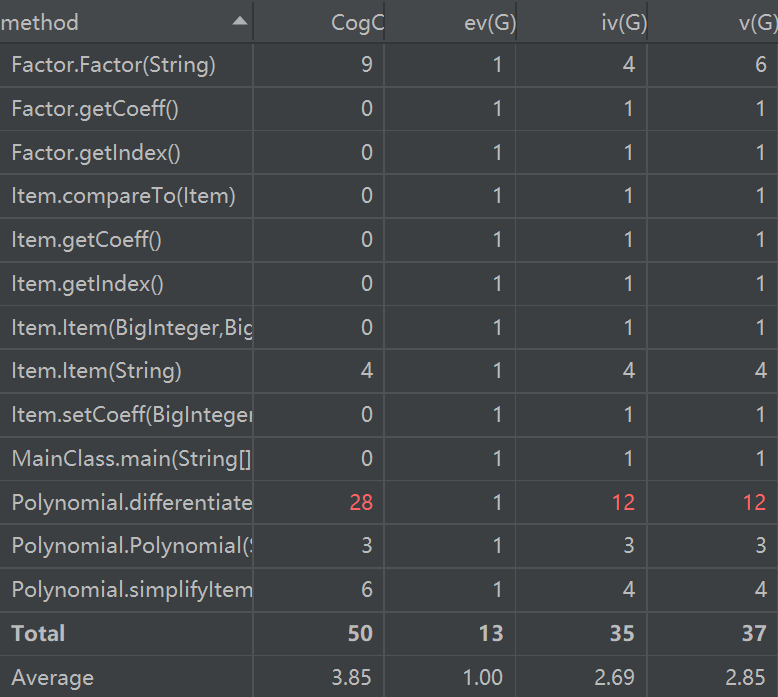
求导方法的处理不是很完美，耦合度太高，圈复杂度更高。正确做法应该是在每个类中完成求导，在上一级的类中调用求导函数得到结果。但是第一次作业较为简单，我也就没有考虑那么多。(后果是第二次作业女娲补天orz)

相关性度量

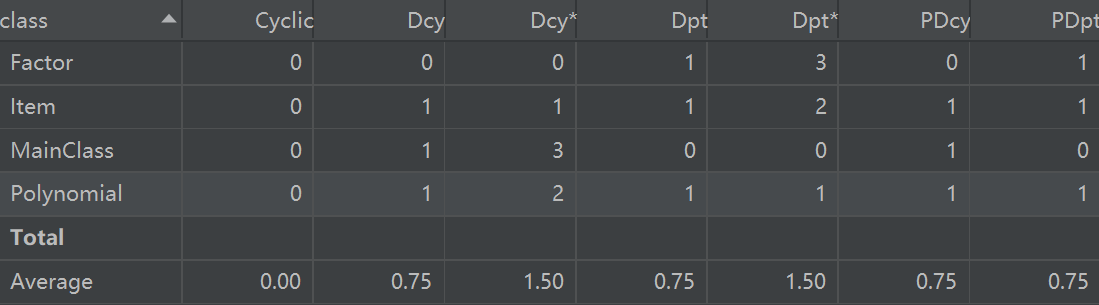
度量分析小结

分析完代码，自己担心的问题果然发生了(当时偷懒写的求导函数明显是面向过程的，写完就觉得不对劲)。这份代码的求导问题没有得到很完美地解决，如果不把求导下放到下一级的类中，带来的复杂度增加是无法解决的。此外，存储数据的方式不限于ArrayList，使用其他存储类型也可以降低复杂度(比如HashMap)。当然，这次作业也存在优点，对表达式的解析过程十分清晰，类与类的关系简明。

程序bug分析

这次作业很幸运，没有出现bug。我在课下与另一位同学(@qlh)合作完成了一个简单的评测机，通过大量数据测试，证明了程序的可靠性与正确性，也为后续的互测准备了工具。

互测寻找bug的策略

首先要对题目给出的形式化表述有明确的认知，特别要关注同级(项、因子)之间的连接处可能存在的问题。例如，正负号出现的次数与位置，空格可能出错的位置以及简化表述-x可能存在的问题。

此外，可以自己尝试搭建一个评测系统：利用python或者java的xeger模块，根据所给的正则表达式随机生成表达式；将别人或自己的程序求导结果，与python自带的sympy库求导后的结果进行对比，发现存在的问题。

第二次作业

第二次作业在上一次的基础上加入了正余弦函数与表达式因子：

• 因子 → 变量因子 | 常数因子 | 表达式因子
• 变量因子 → 幂函数 | 三角函数
• 表达式因子 → '(' 表达式 ')'
• 三角函数 → sin 空白项 '(' 空白项 x 空白项 ')' [空白项 指数] | cos 空白项 '(' 空白项 x 空白项 ')' [空白项 指数]

一开始读完题目，我是绝望的 T ^ T......题目对因子做了增加，这表示我第一次作业拆分因子的方式将会完全无效，再三考虑之后，我选择了重构。题目中，表达式因子的出现，使得通过正则表达式拆分项与因子不再可行，因此我们不得不选择其他方法处理表达式串。一种可行的方法是递归下降分析，笔者尝试过使用该方法，但无奈看不太懂网上的教程，最终选择了一种类似递归下降的方法。

程序架构与实现方法

重构之后，程序新增了以下几个类：正弦函数类(Sin)、余弦函数类(Cos)、幂函数类(Power)、常数类(Const)、工厂类(Factory)、字符串处理类(StringProcess)。同时，我也对先前一些类的内容与类之间的关系做了相应的调整。

程序的UML图

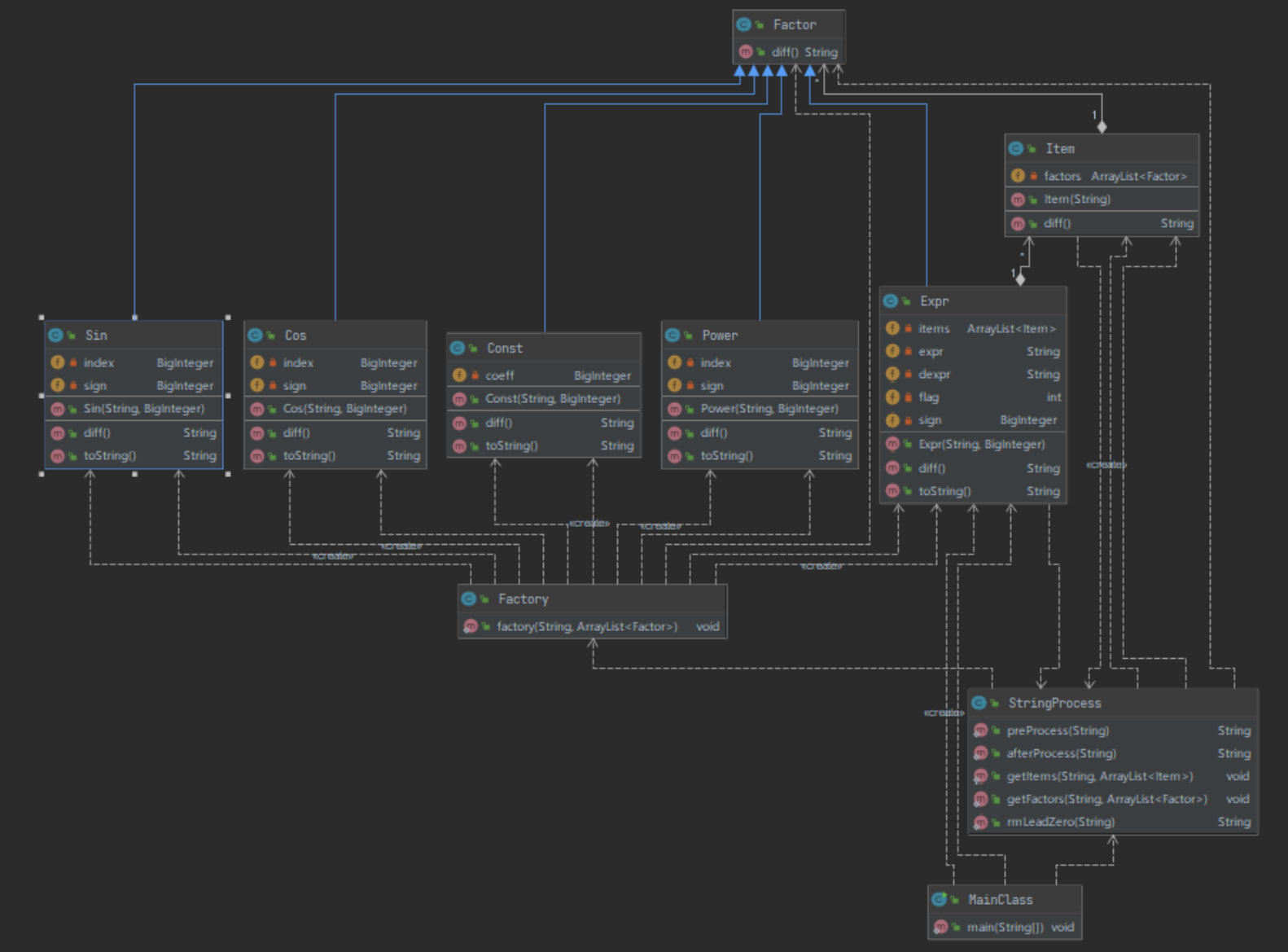
最终我采用的方法是，Expr类、Power类、Sin类、Cos类、Const类继承Factor类，均实现difff()方法进行求导，再一级一级向上传递求导后的表达式字符串，在每一级中进行字符串的拼接与化简。其中，拆分项、因子、表达式预处理和结果串处理的过程交给StringProcess类。

整个程序的最终架构比第一次复杂了许多，由于表达式因子的存在，Expr类既要存放主表达式，又要处理表达式因子，就会显得比较庞大，关系较为复杂。此外，新建Sin与Cos类，也为后续的开发工作留下了充足的余量，尽力避免再一次重构。

表达式类(Expr)

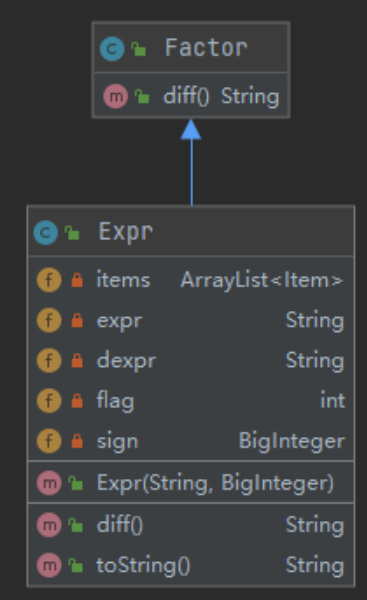
还是用ArrayList存放项，用expr、dexpr分别存放求导前和求导后的表达式字符串，sign用来记录该表达式前的符号(为了处理表达式因子的符号问题)，flag则是用来标记求导与否。flag的出现大大减少了递归的次数，这也与我后面debug部分相关)

正弦&余弦函数类(Sin & Cos) & 幂函数类(Power)

三角函数与幂函数的处理基本相似，这里拿Sin类举例。

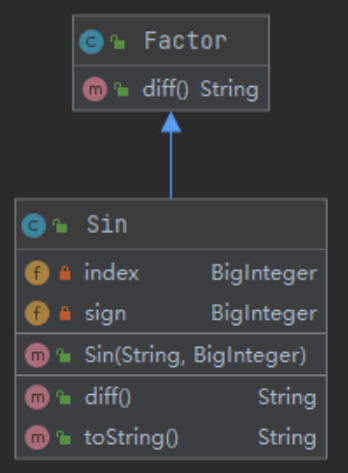
index记录三角函数的指数，sign记录前面的符号。在Sin()方法中，通过正则表达式获取index与sign。

工厂类(Factory)

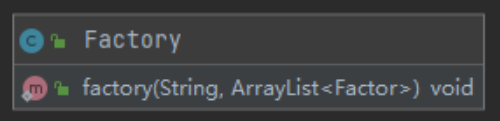
工厂类通过读入字符串与链表，将字符串转换为因子存放到链表中。在具体处理时，考虑到传入的因子带有正负号，我在读取时先记录第一位可能存在的符号，让每一个继承Factor的类都拥有一个sign成员，这样在新建因子对象的时候就可以带着符号一起递归了。

字符串处理类(StringProcess)

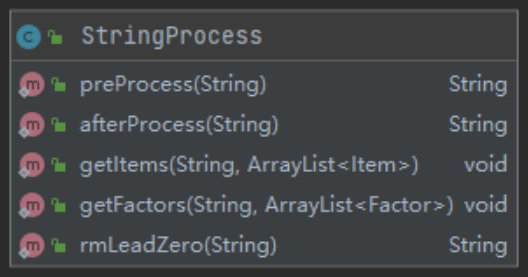
preProcess()对输入串预处理，去除空格并替换**(这里在后面一次作业中存在一定隐患)；afterProcess()处理结果串中一些自己替换的符号；getItems()与getFactors()用来拆出项与因子；rmLeadZero()去除结果串中的前导零。

结果化简

这次由于我使用的方法返回的内容是字符串，导致一部分的化简工作很难开展。在反复权衡之后，我在性能与正确性之间，选择了正确性。我做的化简工作主要是，去除一小部分多余的括号，去除前导零，将乘法含0的表达式或项或因子删除。

多于括号可能出现的地方，在于每一级向上返回的地方，即diff()函数。比如，一个因子返回到项时，如果是表达式因子则需要加括号，如果不是则不需要。通过正则表达式等手段，可以对这些特殊情况做判断，不用无脑添加括号。

含0项删除则是可以在合并求导串的时候完成。如果读取到某个因子的导数为0时，可以直接跳过这一层循环。

程序结构的度量分析

类度量分析

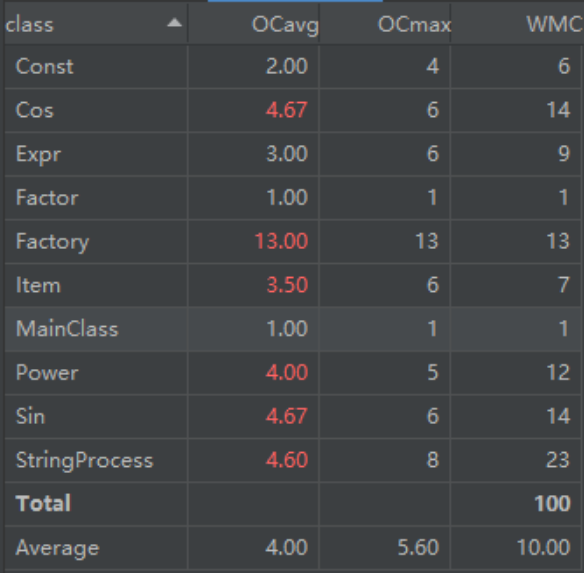
从表格可以看出，复杂度最高的，都是与因子相关的类(要么本身是因子，要么适用于生成因子)。在我使用的这个方法中，这样的复杂度很难避免，表达式因子的存在使得递归无法避免。这张图是我debug后的度量图，之前的代码忘记给Expr做求导标记了，复杂度应该直接爆表了......麻了orz

方法度量分析

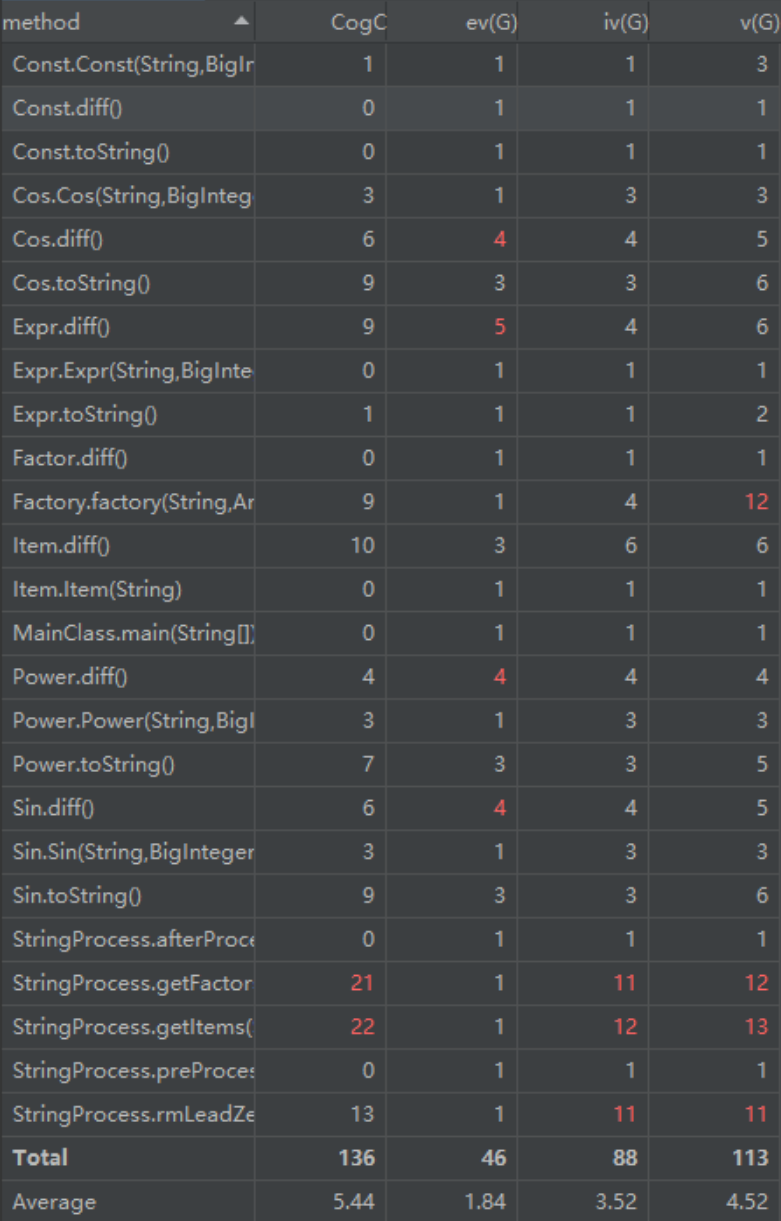
复杂度较高的方法几乎都与求导有关，这可能是应为我在求导函数中加入了部分的化简工作，导致性能较低。其中复杂度最高的两个函数是用来拆项和因子的，写法还是按照面向过程的方式来写的，存在多层循环嵌套。

相关性度量

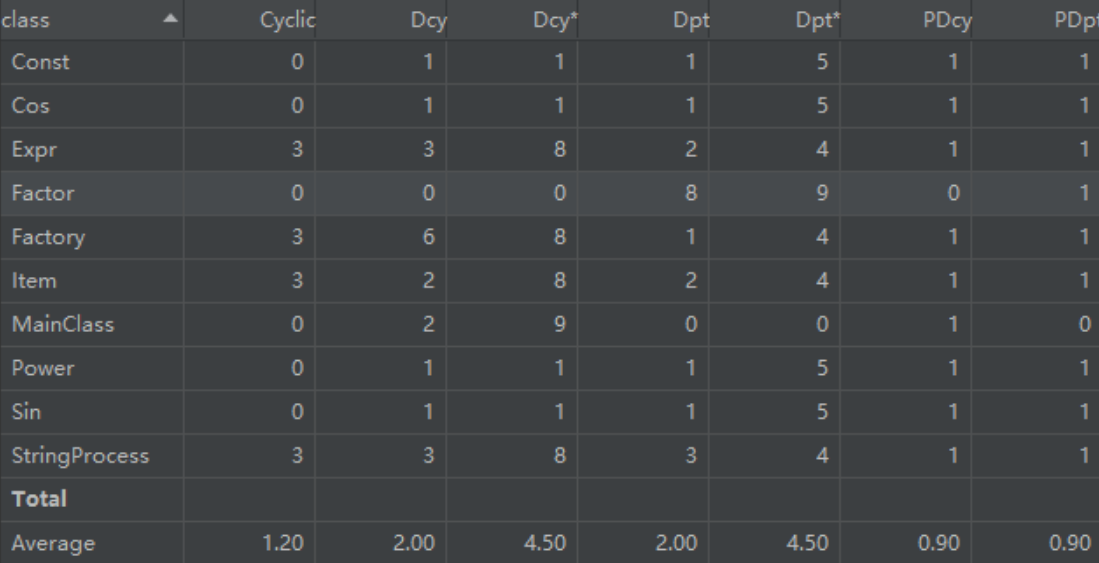
度量分析小结

综合来看，圈复杂度过高主要是面向过程的拆分方式的锅以及递归算法的锅。但是由于无法摆脱递归(至少我没想到有啥办法)，也只能妥协牺牲掉运算时间。我能想到的提高的地方，或许可以尝试不拼接，而是直接一部分一部分地输出结果（感觉不太可行...）？但是看看其他的类，他们地复杂度小了很多，说明编写的时候充分考虑了，避免了一些高耗时的写法。通过后期评测的CPU时间（0.x秒/2秒）来看，这样的写法还是在可接受范围内的。

程序bug分析

由于自己的太懒太摸太不走心，这次作业可算是出锅了。强测TLE了2个点，分数直接爆炸。在互测时，有同学用 ((((((((((((((((((((sin(x))))))))))))))))))))) 这样的数据再次让我TLE了（不过这位同学很讲武德，没有重复hack我这个错误，感谢感谢）。

这种问题在自己做测试的时候就发现了，有些数据点跑半天也出不了结果，当时自己觉得强测不会有这样大的数据 ，也就懒得去改这个问题了。

修复的那几天，起初我以为是递归算法不可行，以至于差点放弃bug修复。在经过尝试与思考之后，我怀疑可能是Expr类存在问题。debug时，我用稍微弱一点的括号嵌套去单步调试，发现Expr类中做了很多次无谓的求导，最后我通过加入上文提及的flag标记是否完成求导，解决的递归求导的冗余问题。

各位读者也要以此为戒，用到递归的时候一定要检查是否存在重复计算。

互测寻找bug的策略

寻找别人的bug，本质上也能检验自己的思维是否正确。这次的bug存在的地方和第一次差不多，但是也可能会有数组越界、运算超时等问题。嵌套的处理是否完美，表达式因子前的符号问题，都应该是hack时应该关注的点。

重构心得体会

由于第一次作业在构建时，没有很好的考虑后期的迭代开发，第二次作业我选择了重构。重构时，我将欠缺考虑的Factor类转变为父类，将各种因子抽出建立子类，这样就很好的实现了继承关系，也方便对各个不同的因子做统一的管理。重构初期，我其实是非常纠结的，我也想过是否能在第一次代码的基础上，利用一些面向过程的方法来完成第二次的要求。这样虽然可行，但是考虑到后续第三次作业，我最终没有选择这种妥协的办法。在重构时，一定要吸取先前架构的优点，也要发现存在的结构性问题。当然，虽说不要轻易重构，我们也要正确看待重构，不要小瞧它的威力。

第三次作业

第三次作业对比上一次，加入了三角函数的嵌套以及表达式格式检查。

• 三角函数 → sin 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数] | cos 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数]

先前重构之后的代码考虑到了这种可能，因此这次作业就相对轻松不少了，运算方面只要对三角函数类做一点小小的的增量修改就行。

程序架构与实现方法

第三次作业没有新加其他的类，只是对现有的类添加了一些内容，增加了格式检查的静态方法。主要修改的类有Sin类，Cos类，Power类，StringProcess类。

程序的UML图

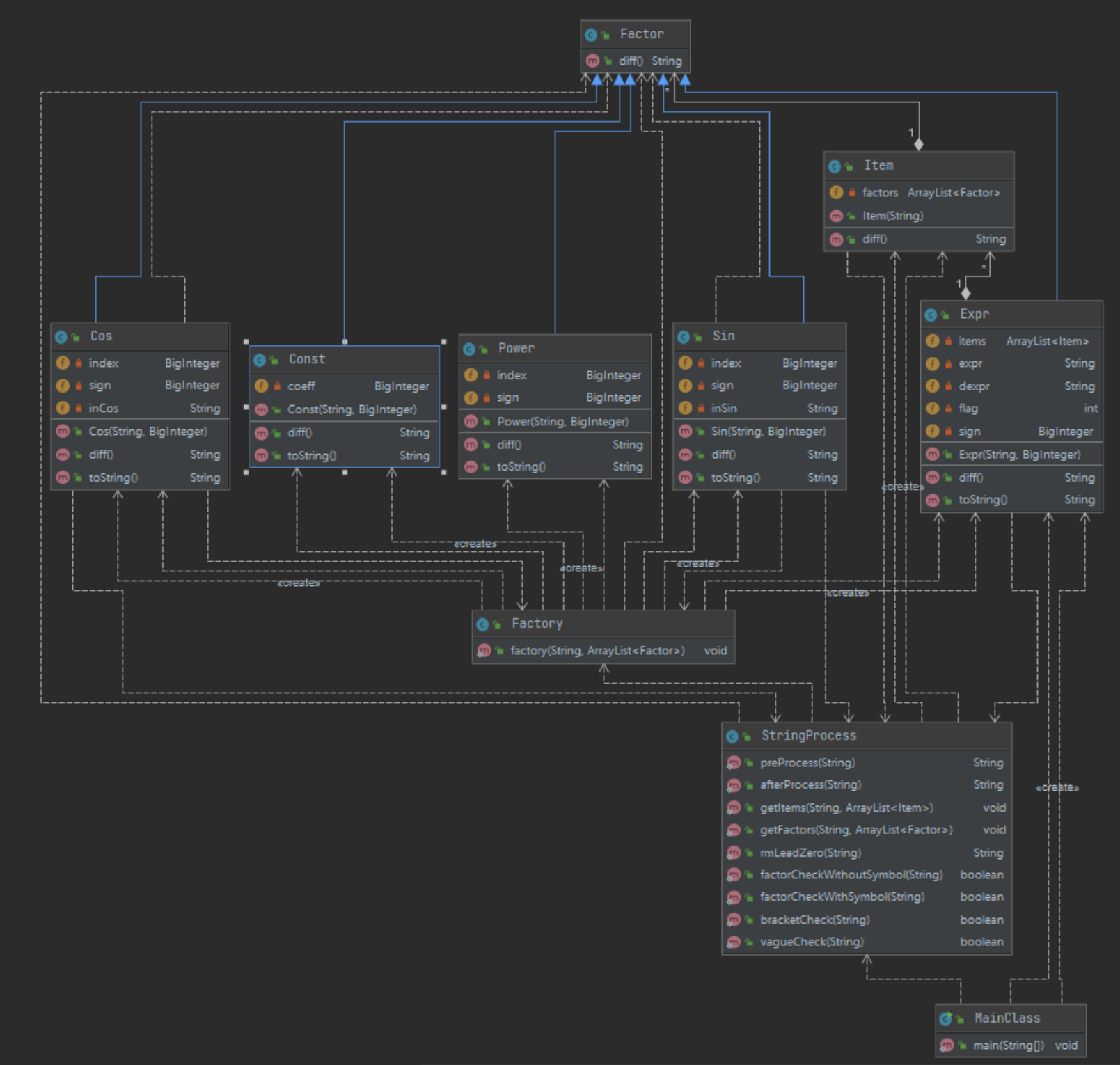
可以看出，程序结构与第二次不尽相同。部分类由于加入了格式检查方法，显得略有些臃肿。下面我会选出改动比较大的2个类，给出相应的解说。

三角函数类(Sin & Cos)

这里以Sin类为例。

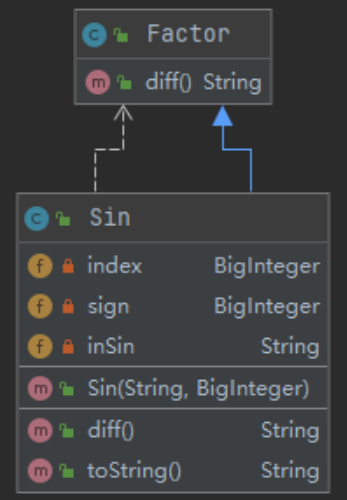
三角函数类我添加了一个inSin成员，用来存放sin括号内的因子。同时，在Sin()方法读入的时候，先判断指数是否在要求的范围内，再调用StringProcess.factorCheckWithoutSymbol()方法判断括号内是否为合法的因子。

字符串处理类(StringProcess)

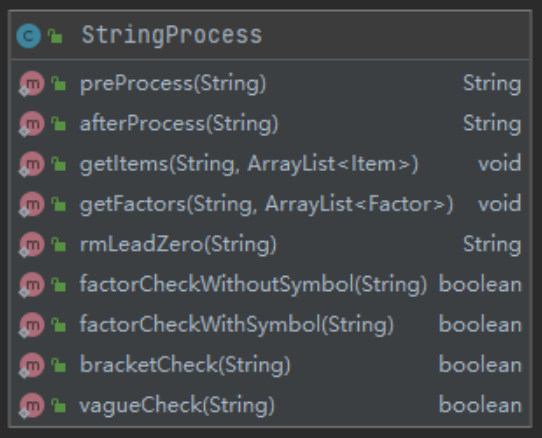
增加了factorCheckWithoutSymbol()、factorCheckWithSymbol()、bracketCheck()、vagueCheck()方法。前两个检查因子的方法几乎相同，差别仅仅在于第二个方法是带符号判断，用在拆项方法getFactors()中做格式检查。bracketCheck()被上述两个方法调用，用来检查表达式因子。除了检查因子是否合规之外，空格的位置也需要做检查。vagueCheck()通过在输入串中识别可能错误的情况(利用正则表达式)，对格式问题做了一步预处理。

结果化简

这次作业由于是在第二次的基础上增量开发，我也就没有去做进一步的化简工作。具体采用的化简方式请往上看。

程序结构的度量分析

类度量分析

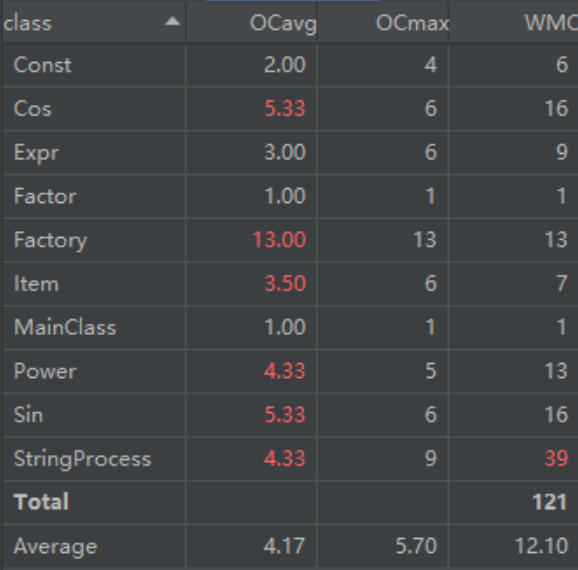
与第二次不同在于，StringProcess类的圈复杂度有了明显提高，这是由于表达式格式检查的时候，bracket()使用了循环嵌套。

方法度量分析

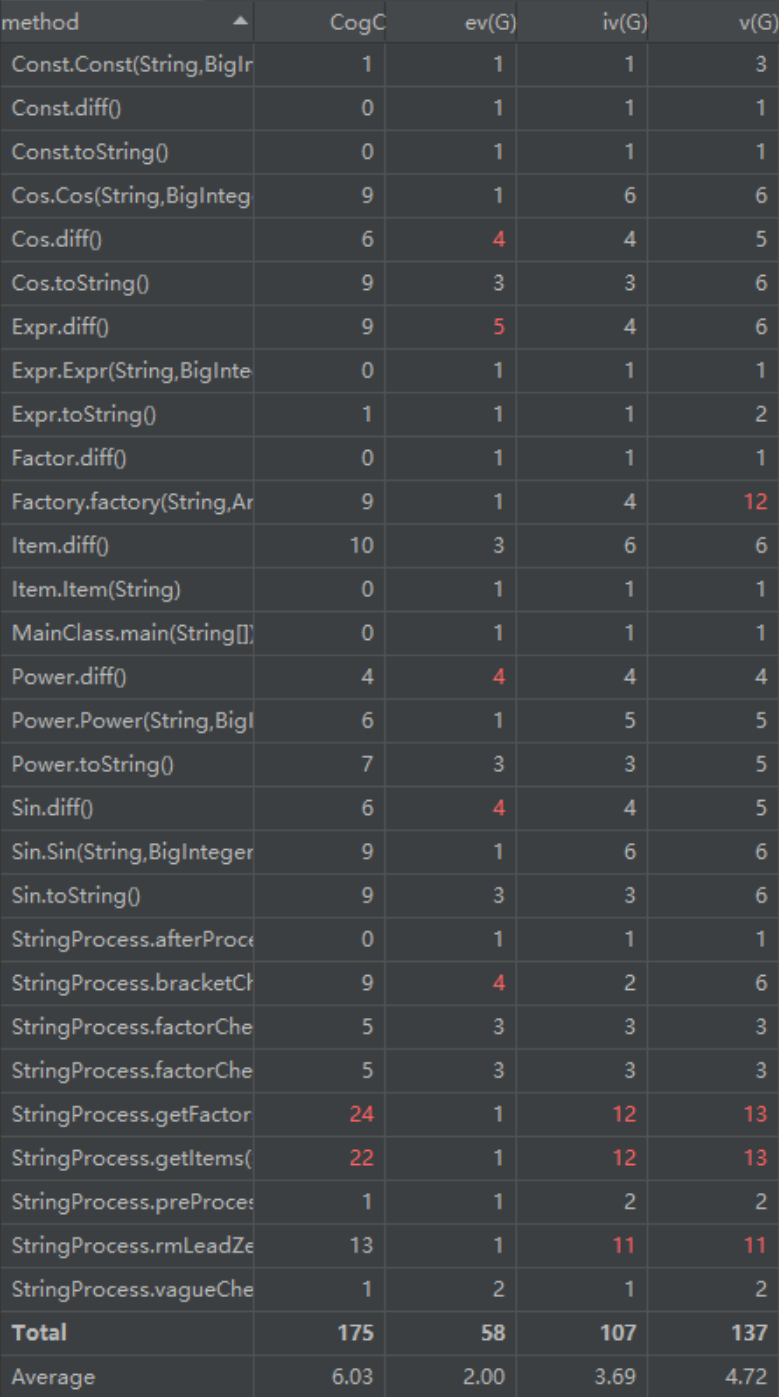
增量开发的部分，只有bracketCheck()方法的复杂度偏高，但也在接受范围内。

相关性度量

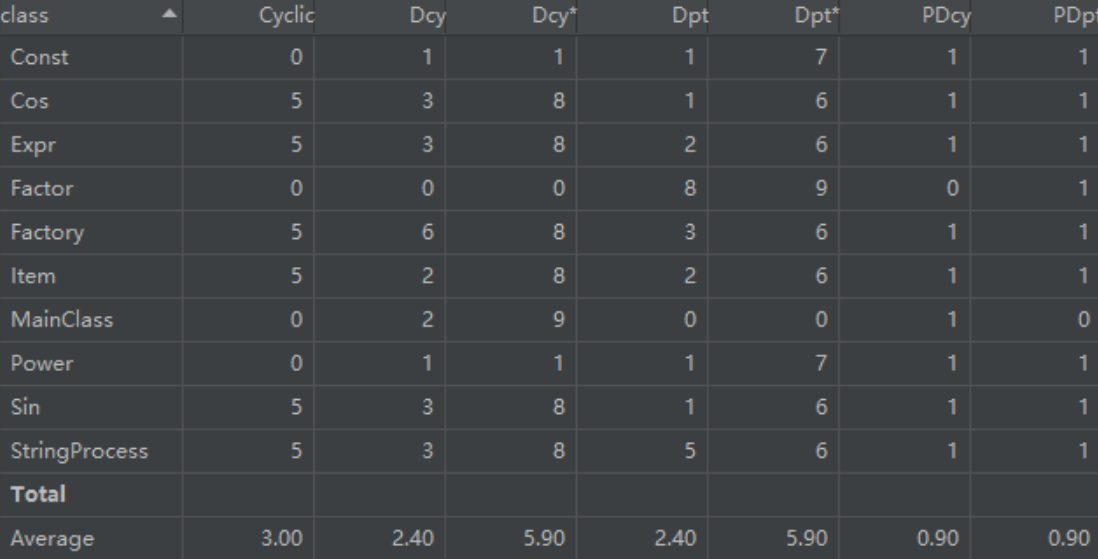
度量分析小结

这次作业基本情况与第二次相同，这里不再赘述。只是，StringProcess中因子检查的两个函数大部分内容相似，可以考虑做一步合并。

程序bug分析

这次作业又双叒叕出问题了。这次的问题不在递归运算的时间上，而是在表达式格式检查的时候少考虑了一种情况：sin(- 1)。三角函数括号内的因子若是带符号的整数，则符号与数字之间不能有多余的空格。

互测寻找bug的策略

这次的作业hack要求有了些提升，使得造数据的工作稍微困难了点。不过，我们阅读题目之后，发现还是可以从以下几个方面入手：

• 带有指数的只能是x或者三角函数，表达式因子不能有幂次
• sin(factor)如果带表达式因子，表达式外的括号必不可少，sin(x*x)这样的输出是错误的！！！上文也有提及，不能在第三次作业无脑替换x**2
• 指数只能是要求范围内的带符号数，不能带括号
• 最多连续出现3个正负号，且最后一个符号后必须有数字，且两者之间不能存在空格
• ......

心得体会

这个单元的三次作业，难度有在逐步提升，虽然完成时有些许痛苦，但是还是让我学到了面向对象的基本思想，也让我接触到了一些新的概念与新的学习方式。

三次作业让我对正则表达式有了更深入的理解，表达式树的思想帮助复习了数据结构相关内容，递归下降算法等解决方案也开拓了我的眼界。

从过程来看，工作前期的充分思考与遇到困难时的慎重选择(包括重构，部分重写)，对于程序开发来说显得尤为重要。如果开发程序时只将眼光放在当下，那么开发出的程序几乎是无法进行功能性提升的。从某种角度来说，这也是对我们超前思维与预判能力的一个考验。

希望有了第一单元的经验与教训，在后面的几次作业中，我能更加小心谨慎、考虑周全吧。