NOI Online 题解
Noi Online 题解 (TG)
T2 冒泡排序
0.前言
这是一道非常常规,非常套路的数据结构题
对于这一类题 解决它有三 四 步
- 分析性质
- 应用性质
- 数据结构优化
- 开 long long
1.分析性质
结论 : 对于一个 1~n 的任意排列 P ,令 其 第 i 位 的逆序对 Si ,一轮冒泡排序后 第 i 位的逆序对个数位 SSi
满足 经过一轮冒泡排序 SSi =max( 0 , Si+1 - 1 ) 且 SSn = 0
如果 不够形象 ,可以举个例子 : 对于 1~5 的排列 P : 1 , 3 , 5 , 2 , 4
他的 S : 0 ,0 ,0 ,2 ,1
经过一轮冒泡排序 P' : 1 , 3 , 2 , 4 , 5
他的 S': 0 ,0 ,1 ,0 ,0
你可以把 S 和 S’ 对照着看 :
0 ,0 ,0 ,2 ,1,
0 ,0 ,1 ,0 ,0
是不是满足上述关系?问了也白问,当然满足
对于这个性质 , 这里给出以下证明 :
证 : 对于一个 1~n 的任意排列 P ,令 其 第 i 位 的逆序对 Si
一轮冒泡排序后 第 i 位的逆序对个数位 SSi
每一轮 冒泡排序 的 具体 过程 可以抽象为 :
- 以 第一个数 为 当前最大值 x;
- 将 这个数 移至 第一个比 当前最大值 x 大 的数 y 的 前一个位置 , 并把 中间的数 向前移动 一个单位;
- 如果还未到最后一个 以 y 为新的 当前最大值 x,重复第二步;如果已经达到最后一个 , 结束排序
我们可以发现 , 对于 这样 的 “三步循环版冒泡排序” ,每一次 “三步循环” 中 ,有 两种 不同的数
分别是 : 当前最大值 x(红体), 中间的数(黄体),
(ps:至于 比当前最大值 x大的数 y ,由于它会成为下一次“三步循环” 中 的 当前最大值 x ,所以不做考虑)
对于 当前最大值 x ,经过移动后 , 它的逆序对数为 0(即他前面没有比他大的数)
其实可以这么想 : 因为 x 能被选为 当前最大值 , 即说明 ,他本身就是 前面最大的数 ,
以此及彼 , 可知 : y 之前也没有比 y 大的数 ,
所以 Sy的位置 = 0 , 所以 SSx被移到的位置 = 0 是符合我们的结论 SSi =max( 0 , Si+1 - 1)。
而对于 中间的数 ,在位置的改变上 , 它 仅仅 只是向前移动了 一个单位
至于逆序对个数 ,在 当前最大值 x 现在被移到了后面 ,本来它 与每一个 “中间的数” 都能组成 一组逆序对 , 而现在由于冒泡排序 ,两者被拆散了
所以 SS每一个中间的数,向前移动一个单位后的位置 = S每一个中间的数,原来的位置 - 1 这也是 符合 我们的结论的 。
这样我们就证明了, SSi =max( 0 , Si+1 - 1 )
至于 SSn = 0 …… 其实你只要令Sn+1 = 0 就行了
假若真的要证明 , 其实可以用冒泡排序的定义 : 每次选出无序部分中最大的,放在有序部分的最前面
(这个不理解的,请再去温习一下冒泡排序)
这样的话 , 即便你只进行了一轮 冒泡排序 后 ,就已经有了 SSn = 0 了。连我都觉得不是很清楚,你们还是令Sn+1 = 0吧
证毕。
下面可以投入使用了。
2.应用性质(假设计算经过 k 轮冒泡排序后……)
如果你直接应用上述性质,用O(n*k) 的时间复杂度制造 k 轮后的逆序对数列 ,你将得到 10 分 ≌ 暴力
既然我们要求的是逆序对总数 , 那么我们需要准换!!!
假设 我们 已经知道了 原序列的 逆序对总数sum 和 逆序对数列 S
如果 所有 的 SSi 都等于Si - 1 的 话 ,答案就很好考虑 ,即 ans = sum-k*n
但很明显 ,不是所有的 Si 都支持 减 k 次 1
同样明显 , 我们可以发现 只有满足 Si >= k ,才能够减 k 次 1 ; 而其他 Si 最多 也是能减 Si 次
再看看我们最早给出的式子 ans=sum - k*n 其实是多减了
那多减了多少呢?
请大家借助一下这幅图(白色为多减的部分)
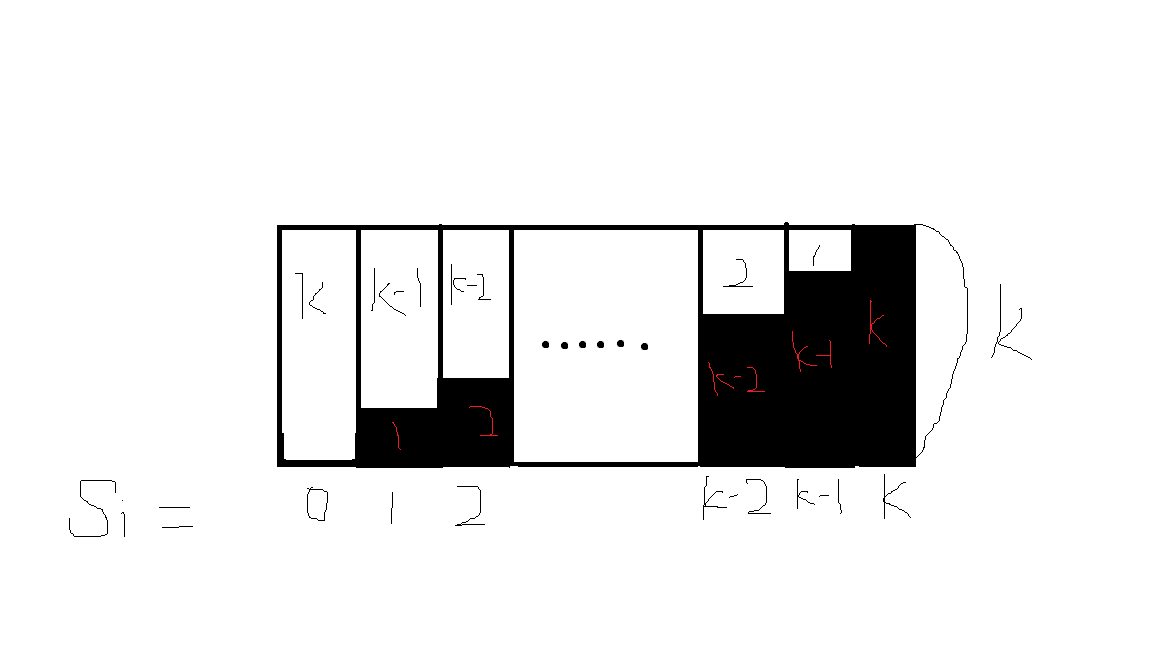
可以发现 对于 Si = 0 时 我们多减了 k ,对于 Si =1 时 我们多减了 k -1 ,对于 Si = k-1 时 我们多减了 1
我们不妨用一个桶 fi , 来统计 Si = i 出现的个数 ,
即 多减部分 = ∑k-1i=0 (k - i) * fi
有了这个式子 , 我们就能推出 答案 为 ans=n - k*n + 多减部分
3.数据结构优化
如果直接使用上述的答案式子 ,单词询问 的 时间复杂度是 O(n) 的 , 你将获得 40 分 , 等价于 两个暴力
现在考虑用数据结构优化上述表达式
我们发现 , 原先 40 分 算法的复杂度瓶颈 在于 计算多减部分 , 唯独可以被优化的 ,也只有这一部分了
由于这是一个很常规的树状数组优化,如果你已经想到,可跳过下一段
我们可以发现 , 式子 多减部分 = ∑k-1i=0 (k - i) * fi ,可以变形为 :多减部分 = [ ∑k-1i=0 (n-i)* fi ] - (n - k ) * ( ∑k-1 i=0 fi ) 因式分解后可变回原式
而 变形后的的式子 , 前一部分 和 后一部分 都能用树状数组维护 。
看一下这幅图可以帮助理解 :
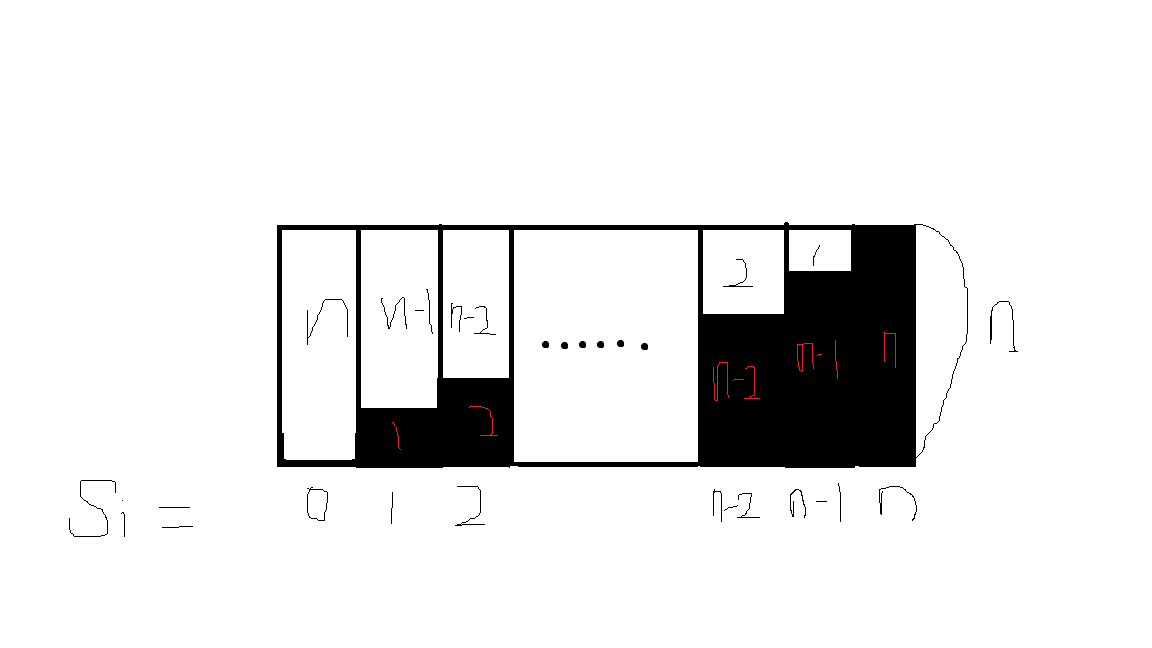
我们可以用树状数组维护白色部分
再看下图 :
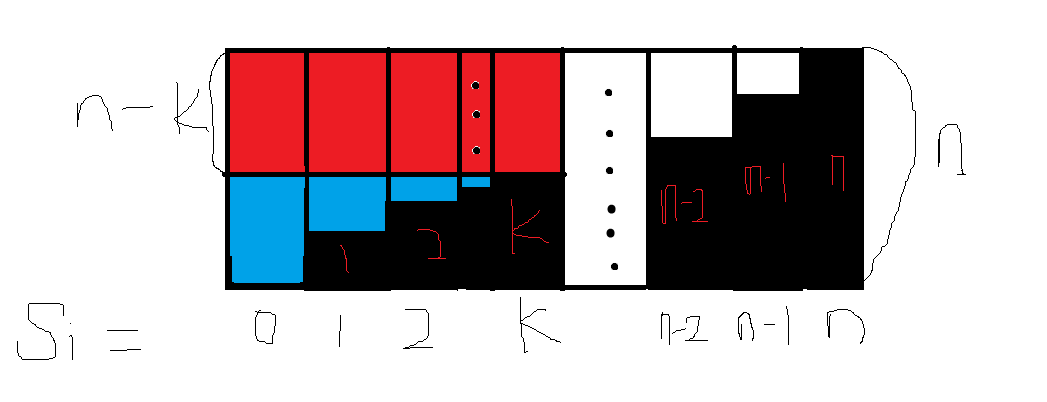
在上图中 , 我们可以看到 , 真正的多减部分是蓝色的部分 , 而我们用树状数组统计的, 是 红色 与 蓝色 部分的总和 , 所以要减到 红色部分 。
以上所谈论的 , 使得单次询问的时间复杂度 优化到了O( logn ) 了
这部分代码如下 :
if (x>=n) // 冒泡排序最多进行 n-1 次 { puts("0"); continue; } printf("%lld\n",sum-x*n+(C::ask(x)-B::ask(x)*(n-x)));
4. 关于修改操作
题中的修改 是指 将 第 x 个位置, 与 第 x + 1 个位置 相交换
在前文中 , 我们已经有了用两个树状数组求答案的方法 , 现在我们要做的 , 就是更新这两个树状数组 。
由于 这两个树状数组都和 fi 有关 , 而 fi 又和 Si 有关 ,Si 又和 交换后的序列P 有关 。因而我们一一考虑。
对于 Px 和 Px+1 , 直接交换即可
交换 Px 和 Px+1 后 ,我们发现 影响只存在于新的 Sx 和 Sx+1 之间,
- 如果 Px 和 Px+1 本身就是一组逆序对 , 那么交换后 这组逆序对就消失了, 即 新的 S x = 原来的S x+1 - 1 ,Sx+1 = 原来的 Sx
- 如果 Px 和 Px+1 本身是有序的 , 那么交换后 这两个就会产生 一组逆序对 , 即 新的 S x+1 = 原来的 S x + 1 ,Sx = 原来的 Sx+1
再看 fi , 这个比较方便 , 你只要把 原先的Sx 和 Sx+1 在桶内的值删去 , 加上 新的Sx 和 Sx+1 的贡献 。
至于两个树状数组 , 也一样 ,先把原先的 fx 和 fx+1 的贡献删除 ,加入 新fx 和 fx+1 的 贡献 。
这部分代码如下
swap(ans[x], ans[x + 1]); if (a[x]>a[x+1])// 原先就是逆序对 { f[ans[x]]--; B::add(ans[x]+1,-1); C::add(ans[x]+1,ans[x]-n); ans[x]--; C::add(ans[x]+1,n-ans[x]); B::add(ans[x]+1,1); f[ans[x]]++; sum--; } else // 原先不是逆序对 { f[ans[x+1]]--; B::add(ans[x+1]+1,-1); C::add(ans[x+1]+1,ans[x+1]-n); ans[x+1]++; C::add(ans[x+1]+1,n-ans[x+1]); B::add(ans[x+1]+1,1); f[ans[x+1]]++; sum++; } swap(a[x], a[x+1]);
5. Code Time
#include<bits/stdc++.h>
#define MAXN 2000007
#define LL long long
using namespace std;
int n,m;
LL sum,f[MAXN],ans[MAXN],a[MAXN];
namespace A
{
LL c[MAXN];
void add(int x,LL y)
{
for (;x<=n;x+=x&(-x)) c[x]+=y;
}
LL ask(int x)
{
LL res=0;
for (;x;x-=x&(-x)) res+=c[x];
return res;
}
}
namespace B
{
LL c[MAXN];
void add(int x,LL y)
{
for (;x<=n;x+=x&(-x)) c[x]+=y;
}
LL ask(int x)
{
LL res=0;
for (;x;x-=x&(-x)) res+=c[x];
return res;
}
}
namespace C
{
LL c[MAXN];
void add(int x,LL y)
{
for (;x<=n;x+=x&(-x)) c[x]+=y;
}
LL ask(int x)
{
LL res=0;
for (;x;x-=x&(-x)) res+=c[x];
return res;
}
}
signed main()
{
scanf("%d %d",&n,&m);
for (int i=1;i<=n;i++) scanf("%lld",&a[i]);
f[0]=1;
ans[1]=0;
A::add(a[1],1);
B::add(1,1);
C::add(1,n);
for (int i=2;i<=n;i++)
{
int x=A::ask(n)-A::ask(a[i]);
f[x]++;
ans[i]=x;
sum+=x;
A::add(a[i],1);
B::add(x+1,1);
C::add(x+1,n-x);
}
for (int i=1;i<=m;i++)
{
int op,x;
scanf("%d %d",&op,&x);
if (op==1)
{
swap(ans[x], ans[x + 1]);
if (a[x]>a[x+1])
{
f[ans[x]]--;
B::add(ans[x]+1,-1);
C::add(ans[x]+1,ans[x]-n);
ans[x]--;
C::add(ans[x]+1,n-ans[x]);
B::add(ans[x]+1,1);
f[ans[x]]++;
sum--;
}
else
{
f[ans[x+1]]--;
B::add(ans[x+1]+1,-1);
C::add(ans[x+1]+1,ans[x+1]-n);
ans[x+1]++;
C::add(ans[x+1]+1,n-ans[x+1]);
B::add(ans[x+1]+1,1);
f[ans[x+1]]++;
sum++;
}
swap(a[x],a[x+1]);
}
else
{
if (x>=n)
{
puts("0");
continue;
}
printf("%lld\n",sum-x*1LL*n+(C::ask(x)-B::ask(x)*1LL*(n-x)));
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号