最近在学习redis, 看到hyper loglog 有这么近乎作弊的空间复杂度
着实好奇
其核心使用了概率统计 通过局部判断总体
- loglog
我们的任务是基数统计 判断不重复子串数量
字串由0/1排列而成
这就是典型的二项分布, 分布概率均为1/2
那不就是正态分布
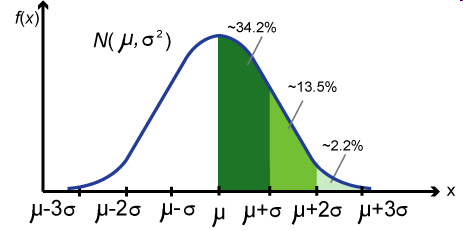
当0与1数量相差小时集中在 x = μ上 当0与1数量相差大时集中在两端
可见当字串0/1分布越极端概率越小
假设 μ左侧为1多情况, μ右侧为0多情况
我们仅取一端 0多情况 简单用局部(50%)估计总体(100%)
而hyper loglog采用的就是 从右向左数没遇到1时数的0的个数m 保存这段数据中Max(m1, m2, …)
Max(m1, m2, …)中0的个数越多概率越小 反应基数数据量越大
- hyper 部分
针对了极端情况进行了优化
当基数极小却意外取到了大量的0 ,那基本就gg了
此时我们将数据分片, 每个片再依次求基数量, 取平均数 * 片数量
调和平均数 和 一般平均数
倘若 A工资为 1000 B工资为 30000
一般平均数下 工资为 ( 30000+1000 ) / 2 = 15500
而调和平均数 2/( 1/1000 + 1/30000 ) ≈ 1935.484
显然在调和平均数的计算下 更不容易受到大值的影响
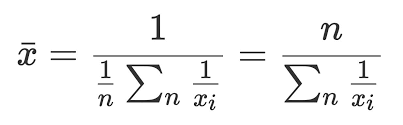
调和平均数
即有公式




 浙公网安备 33010602011771号
浙公网安备 33010602011771号