恨7不成妻

恨 7 不成妻

题目描述

单身！
依然单身！
吉哥依然单身！
DS 级码农吉哥依然单身！
所以，他平生最恨情人节，不管是 214 还是 77，他都讨厌！

吉哥观察了 214 和 77 这两个数，发现：

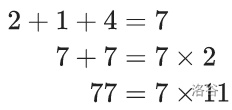
最终，他发现原来这一切归根到底都是因为和 7 有关！所以，他现在甚至讨厌一切和 7 有关的数！
什么样的数和 7 有关呢？如果一个整数符合下面三个条件之一，那么我们就说这个整数和 7 有关：

1. 整数中某一位是 7；
2. 整数的每一位加起来的和是 7 的整数倍；
3. 这个整数是 7 的整数倍。
   现在问题来了：吉哥想知道在一定区间内和 7 无关的数字的平方和。

输入

输入数据的第一行是测试数据组数 T，然后接下来的 T 行表示 T 组测试数据。
每组数据在一行内包含两个正整数 L, R。

输出

对于每组数据，请计算 [L,R] 中和 7 无关的数字的平方和，并将结果对 \(10^9+7\) 取模后输出。

样例输入

3
1 9
10 11
17 17

样例输出

236
221
0

数据范围与提示

对于全部数据 \(1 \le T \le 50\) ，$ 1 \le L \le R \le 10^{18} $ 。

解题思路

可以用记忆化搜索。

int dfs(int len, int mod, int sum, bool fp)

len:当前搜索到了第几位。
mod:当前搜出的数模7的余数。
sum:当前搜索到的数的各位之和。
fp:当前这一位有没有达到上界(true:达到了，false:没达到)。

for (int i = 0; i <= fpmax; i++)
{
        if (i == 7)
            continue;
        int re;
        re = dfs(len - 1, (mod * 10 + i) % 7, (sum + i) % 7, fp && i == fpmax);
}

fpmax:当前这一位的最大值。(如:1234，第一位是1，第二位是2)。
i:这一位选的数。

因为题目上说要求平方和，所以我们还得推出公式:
举个例子，求\(30\) ~ \(34\)的平方和：

\[\begin{aligned} &30^2+(30+1)^2+(30+2)^2+(30+3)^2+(30+4)^2\\ &30^2+(30^2+2*30*1+1^2)+(30^2+2*30*2+2^2)+(30^2+2*30*3+3^2)+(30^2+2*30*4+4^2)\\ &30^2*5+2*30*(0+1+2+3+4)+0^2+1^2+2^2+3^2+4^2 \end{aligned} \]

我们发现如果想求出答案，必须知道三个数：

1. $0+1+2+3+..+(L-R) $ \((0+1+2+3+4)\) 和
2. \(0^2+1^2+2^2+3^2+...+(L-R)^2\) \((0^2+1^2+2^2+3^2+4^2)\) 平方和
3. \(L-R+1\) \((5)\) 数量

所以，我们需要一个结构体，维护这三个数:

struct node{
	int sum;//1 和
	int psum;//2 平方和
	int cnt;//3 数量
	void init(){
		cnt=sum=psum=0;
	}
};

显而易见答案就是第二个数(平方和)。

每次搜索就统计这三个变量：

1. cnt:直接累加。
2. sum:每次累加后还要加一个30。\((0+1+2+3+4) -> (30+31+32+33+34)\)
3. psum:根据推出的公式，\(psum=30^2*cnt+2*30*sum+(下一层)psum\)。

ret.cnt=(ret.cnt+re.cnt);
ret.sum=((ret.sum+re.sum)+((re.cnt*i)*po[len]));
ret.psum=(ret.psum+re.psum);
ret.psum=((ret.psum+(((po[len]*po[len])*i*i)*re.cnt)));
ret.psum=(ret.psum+((2*po[len]*i)*re.sum));

po:po[1]=10,po[2]=100,以此类推。

代码:

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define Mod 1e9+7
struct node{
	int cnt;
	int sum;
	int psum;
	void init(){
		cnt=sum=psum=0;
	}
};
node dp[100][20][20];
int digit[100];
int po[100];
bool vis[100][20][20];
inline node dfs(int len, int mod, int sum, bool fp)
{
    if (!len)
    {
    	node ret;
    	ret.init();
    	if(mod&&sum%7){
    		ret.cnt=1;
    	}
    	return ret;
    }
    if (vis[len][mod][sum]&&!fp)
        return dp[len][mod][sum];
    node ret;
    ret.init();
    int fpmax = fp ? digit[len] : 9;
    for (int i = 0; i <= fpmax; i++)
    {
        if (i == 7)
            continue;
        node re;
        re = dfs(len - 1, (mod * 10 + i) % 7, (sum + i) % 7, fp && i == fpmax);
        ret.cnt=(ret.cnt+re.cnt)%Mod;
        ret.sum=((ret.sum+re.sum)%Mod+((re.cnt*i)%Mod*po[len]))%Mod;
        ret.psum=(ret.psum+re.psum)%Mod;
        ret.psum=((ret.psum+(((po[len]*po[len])%Mod*i*i)%Mod*re.cnt)%Mod)%Mod)%Mod;
        ret.psum=(ret.psum+((2*po[len]*i)%Mod*re.sum)%Mod)%Mod;
    }
    
    if (!fp){
        dp[len][mod][sum] = ret;
        vis[len][mod][sum]=1;
    }
    return ret;
}

inline int f(int n)
{
    int len = 0;
    while (n)
    {
        digit[++len] = n % 10;
        n /= 10;
    }
    return dfs(len, 0, 0, true).psum%Mod;
}

signed main()
{
    int n; 
    scanf("%lld",&n);
    po[1]=1;
    for(int i=2;i<=20;i++){
    	po[i]=(po[i-1]*10)%Mod;
    }
    for(int i=1;i<=n;i++){
    	int l,r;
    	scanf("%lld%lld",&l,&r);
    	printf("%lld\n",(f(r)-f(l-1)+Mod)%Mod);
	}
    return 0;
}