经典算法 - 回溯法
1. 基本概念
递归和回溯相辅相成。只要有递归,就会有回溯。
回溯法是一种纯暴力的搜索,并不是一种高效的算法。
回溯法可以解决的问题:
- 组合问题
- 切割问题
- 子集问题
- 排列问题
- 棋盘问题
如何理解回溯法
回溯法,都可以抽象为一个n叉树形结构。树的宽度一般就是要处理的集合的大小,树的深度就是递归的深度。
回溯法的模板
回溯法一般没有返回值,方法一般命名为backtracking。
确定终止条件,收集结果。
处理完终止条件,进入单层搜索的逻辑。
void backtracking(Paramters){
if(终止条件){
收集结果;
return;
}
for(集合的元素集){
处理节点;
递归函数;
回溯操作;
}
return;
}
2. 组合问题
力扣第77题。
问题描述
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案。
样例
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
输入:n = 1, k = 1
输出:[[1]]
题解
比如给定n=4,k=2。则

回溯三部曲:
- 确定递归函数的参数及返回值
- 递归的终止条件
- 单层递归的逻辑
代码实现
import java.util.ArrayList;
import java.util.List;
class Solution {
List<List<Integer>> result = new ArrayList<>(); // 存储最终结果
List<Integer> path = new ArrayList<>(); // 存储一条路径上的结果
public List<List<Integer>> combine(int n, int k) {
backtracking(n, k, 1);
return result;
}
public void backtracking(int n,int k,int startIndex){
// 递归终止条件 收集结果
if (path.size()==k) {
result.add(new ArrayList<>(path));
return;
}
// 单层递归的逻辑
// i<=n+1-(k-path.size()) 由 if n-i+1<k-path.size() return; 得来
for(int i=startIndex;i<=n+1-(k-path.size());i++){ // 剪枝
path.add(i); // 处理节点
backtracking(n, k, i+1); // 递归
path.remove(path.size()-1); // 回溯
}
}
}
在回溯做剪枝操作时,一般从循环的范围下手,尽量缩短循环的范围。
3. 组合总和Ⅲ
本题为力扣216题。
问题描述
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
输入输出样例
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
代码实现
import java.util.ArrayList;
import java.util.List;
class Solution {
List<List<Integer>> result = new ArrayList<>(); // 存储最终结果
List<Integer> path = new ArrayList<>(); // 存储当前路径上的节点
public List<List<Integer>> combinationSum3(int k, int n) {
backtracking(k, n, 1);
return result;
}
public void backtracking(int k,int n,int startIndex){
// 结束条件 收集结果
int sum = path.stream().mapToInt(Integer::intValue).sum();
if (path.size()==k && sum==n) {
result.add(new ArrayList<>(path));
}
// if path.size()+9-i+1 < k -> i<=path.size()+10-k
for(int i=startIndex;i<=path.size()+10-k;i++){ // 剪枝
if (path.stream().mapToInt(Integer::intValue).sum()>=n) { // 剪枝
return;
}
path.add(i); // 处理节点
backtracking(k, n, i+1); // 递归
path.remove(path.size()-1); // 回溯
}
}
}
4. 电话号码的字母组合
本题为力扣第17题。
问题描述
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

输入输出样例
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
输入:digits = ""
输出:[]
题解

代码实现
import java.util.ArrayList;
import java.util.List;
class Solution {
List<String> result = new ArrayList<>();
StringBuffer path = new StringBuffer();
public List<String> letterCombinations(String digits) {
if ("".equals(digits)) {
return new ArrayList<String>();
}
List<List<Character>> chars = new ArrayList<>();
char[] charArray = digits.toCharArray();
for (char c : charArray) {
switch (c) {
case '2':
List<Character> l2 = new ArrayList<Character>();
l2.add('a');
l2.add('b');
l2.add('c');
chars.add(l2);
break;
case '3':
List<Character> l3 = new ArrayList<Character>();
l3.add('d');
l3.add('e');
l3.add('f');
chars.add(l3);
break;
case '4':
List<Character> l4 = new ArrayList<Character>();
l4.add('g');
l4.add('h');
l4.add('i');
chars.add(l4);
break;
case '5':
List<Character> l5 = new ArrayList<Character>();
l5.add('j');
l5.add('k');
l5.add('l');
chars.add(l5);
break;
case '6':
List<Character> l6 = new ArrayList<Character>();
l6.add('m');
l6.add('n');
l6.add('o');
chars.add(l6);
break;
case '7':
List<Character> l7 = new ArrayList<Character>();
l7.add('p');
l7.add('q');
l7.add('r');
l7.add('s');
chars.add(l7);
break;
case '8':
List<Character> l8 = new ArrayList<Character>();
l8.add('t');
l8.add('u');
l8.add('v');
chars.add(l8);
break;
case '9':
List<Character> l9 = new ArrayList<Character>();
l9.add('w');
l9.add('x');
l9.add('y');
l9.add('z');
chars.add(l9);
break;
default:
break;
}
}
backtracking(chars, 0);
return result;
}
public void backtracking(List<List<Character>> chars,int index){
if (path.length() == chars.size()) {
String string = String.valueOf(path);
result.add(string);
return;
}
List<Character> list = chars.get(index);
for(int i=0;i<list.size();i++){
path.append(list.get(i));
backtracking(chars, index+1);
path.deleteCharAt(path.length()-1);
}
}
}
5. 分割回文串
本题为力扣第131题。
问题描述
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
输入输出样例
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
输入:s = "a"
输出:[["a"]]
题解

代码实现
import java.util.ArrayList;
import java.util.List;
class Solution {
List<List<String>> result = new ArrayList<>(); // 存储返回结果
List<String> cutList = new ArrayList<>(); // 存储当前路径分割方案
public List<List<String>> partition(String s) {
backtracking(s, 0);
return result;
}
public void backtracking(String s,int startIndex){
if (startIndex == s.length()) {
result.add(new ArrayList<>(cutList)); // 收集结果
return;
}
for(int i=startIndex+1;i<=s.length();i++){
String temp = s.substring(startIndex, i);
if (isHuiwen(temp)) {
cutList.add(temp);
backtracking(s, i);
cutList.remove(cutList.size()-1);
}
}
}
// 判断是否为回文串
public boolean isHuiwen(String str){
int start = 0;
int end = str.length()-1;
while(start<end){
if (str.charAt(start)!=str.charAt(end)) {
return false;
}
start++;
end--;
}
return true;
}
}
6. 复原IP地址
本题为力扣第93题。
问题描述
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
- 例如:
"0.1.2.201"和"192.168.1.1"是 有效 IP 地址,但是"0.011.255.245"、"192.168.1.312"和"192.168@1.1"是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
输入输出样例
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]
输入:s = "101023"
输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
题解

代码实现
import java.util.ArrayList;
import java.util.List;
class Solution {
int cutNum = 0;
List<String> result = new ArrayList<>();
StringBuffer ip = new StringBuffer();
public List<String> restoreIpAddresses(String s) {
backtracking(s,0);
return result;
}
public void backtracking(String s ,int startIndex){
if (startIndex == s.length() && cutNum==4) {
StringBuffer resStr = new StringBuffer(ip);
resStr.deleteCharAt(resStr.length()-1);
result.add(resStr.toString());
return;
}
for(int i=startIndex+1;i<=s.length();i++){
String temp = s.substring(startIndex,i);
if ((temp.length()>=2 && temp.startsWith("0")) || temp.length()>3 || cutNum>3) {
return;
}
int strInt = Integer.valueOf(temp);
if (strInt>=0 && strInt<=255) {
int ipLength = ip.length();
cutNum++;
ip.append(temp + ".");
backtracking(s,i);
ip.delete(ipLength,ip.length());
cutNum--;
}
}
}
}
7. 子集
本题为力扣第78题。
问题描述
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入输出样例
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
输入:nums = [0]
输出:[[],[0]]
题解

代码实现
import java.util.ArrayList;
import java.util.List;
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
boolean endFlag = false;
public List<List<Integer>> subsets(int[] nums) {
backtracking(nums, 0);
return result;
}
public void backtracking(int[] nums,int startIndex){
if (endFlag) { // 结束条件
result.add(new ArrayList<>(path)); // 收集结果
return;
}
for(int i=startIndex-1;i<nums.length;i++){
if (i==startIndex-1) { // 空集
endFlag = true;
backtracking(nums, i+1);
endFlag = false;
}else{
path.add(nums[i]);
if (i==nums.length-1) {
endFlag = true;
}
backtracking(nums, i+1);
endFlag = false;
path.remove(path.size()-1);
}
}
}
}
8. 全排列
本题为力扣第46题。
问题描述
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
输入输出样例
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
输入:nums = [0,1]
输出:[[0,1],[1,0]]
题解

代码实现
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.stream.Collectors;
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
List<Integer> list = Arrays.stream(nums).boxed().collect(Collectors.toList());
backtracking(list);
return result;
}
public void backtracking(List<Integer> nums){
if (nums.size()==0) {
result.add(new ArrayList<>(path));
return;
}
for(int i=0;i<nums.size();i++){
Integer current = nums.remove(i);
path.add(current);
backtracking(nums);
path.remove(path.size()-1);
nums.add(i,current);
}
}
}
9. 全排列Ⅱ
本题为力扣第47题。
问题描述
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
输入输出样例
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
题解

代码实现
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.stream.Collectors;
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
List<Integer> list = Arrays.stream(nums).boxed().collect(Collectors.toList());
backtracking(list);
return result;
}
public void backtracking(List<Integer> list){
if (list.size() == 0) {
result.add(new ArrayList<>(path));
return;
}
for(int i=0;i<list.size();i++){
if (i>0 && list.get(i)==list.get(i-1)) {
continue;
}
Integer current = list.remove(i);
path.add(current);
backtracking(list);
path.remove(path.size()-1);
list.add(i,current);
}
}
}
10. N皇后
本题为力扣第51题。
问题描述
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。

输入输出样例
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
输入:n = 1
输出:[["Q"]]
题解

代码实现
import java.util.ArrayList;
import java.util.List;
class Solution {
List<List<String>> result = new ArrayList<>(); //结果
int[][] chessboard; // 棋盘
public List<List<String>> solveNQueens(int n) {
chessboard = new int[n][n]; // 初始化棋盘,默认0填充
backtracking(n,0);
return result;
}
public void backtracking(int n,int row){
if (row==n) {
List<String> r = new ArrayList<>();
for (int[] chess : chessboard) { // 棋盘转化为字符串形式
String temp = "";
for(int i=0;i<chess.length;i++){
if (chess[i]==0) {
temp = temp + ".";
}else if(chess[i]==1){
temp = temp + "Q";
}
}
r.add(temp);
}
result.add(r); // 收集结果
return;
}
for(int i=0;i<n;i++){
boolean isOk = isVaild(row, i, n); // 判断该位置是否可以放置
if (!isOk) {
continue;
}
chessboard[row][i] = 1; // 处理当前节点
backtracking(n, row+1); // 递归
chessboard[row][i] = 0; // 回溯
}
}
// 判断是否可以放置
public boolean isVaild(int row,int i,int n){
for(int j=0;j<row;j++){ // 判断所在列是否存在皇后
if (chessboard[j][i]==1) {
return false;
}
}
int currentRow = row;
int currentCol = i;
// 判断左上是否存在皇后
while(currentRow>=0 && currentCol>=0){
if (chessboard[currentRow][currentCol]==1) {
return false;
}
currentRow--;
currentCol--;
}
currentRow = row;
currentCol = i;
// 判断右上是否存在皇后
while(currentRow>=0 && currentCol<n){
if (chessboard[currentRow][currentCol]==1) {
return false;
}
currentRow--;
currentCol++;
}
return true;
}
}
11. 解数独
本题为力扣第37题。
问题描述
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
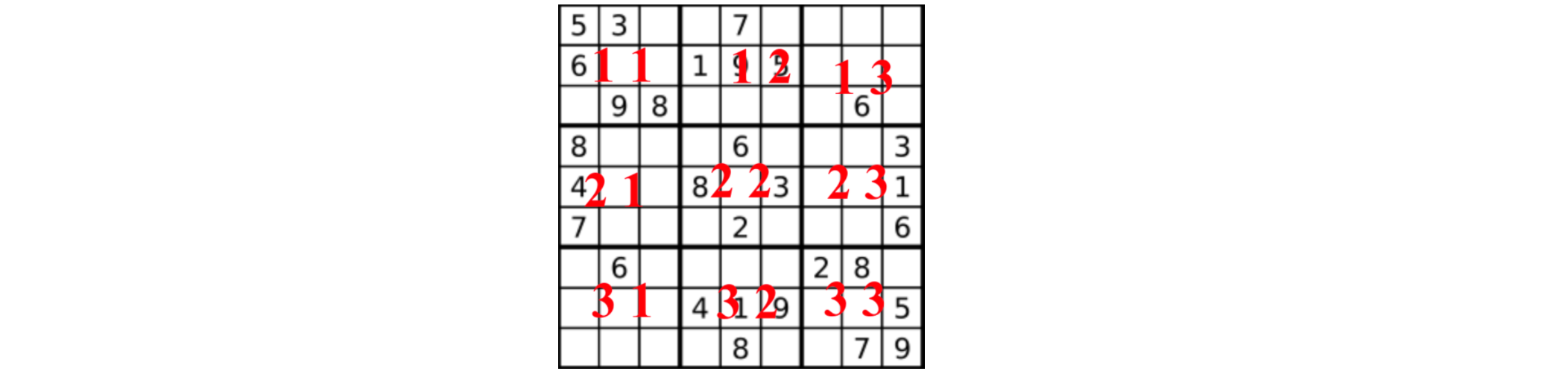
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。

输入输出样例
输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

题解
整体思路:
- 遍历每个位置,判断该位置是否可以放置当前数字(1-9遍历)
判断当前九宫格是否可以放置,处理逻辑:
- 首先获取当前位置所处的九宫格
- 根据当前所处的九宫格得到当前九宫格左上角的元素的位置坐标
- 遍历当前九宫格,判断是否存在相同数值
代码实现
class Solution {
char[][] boardMain;
char[][] result;
public void solveSudoku(char[][] board) {
boardMain = board;
result = new char[9][9];
backtracking(0, 0);
}
public void backtracking(int row,int col){
if (row==9) {
boardMain = result; // 收集结果
return;
}
// 当前位置原来已经存在数字,直接存入,不做处理,处理下一位置
char current = boardMain[row][col];
if (current!='.') {
boardMain[row][col] = current;
result[row][col] = current;
int[] rc = handler(row, col);
backtracking(rc[0], rc[1]);
return;
}
for(int n=1;n<=9;n++){
boolean vaild = isVaild(row, col, n); // 判断当前位置是否可以放置
if (vaild) {
boardMain[row][col] = (char)(n+'0'); // 处理当前位置
result[row][col] = (char)(n+'0');
int[] handler = handler(row, col);
backtracking(handler[0], handler[1]); // 递归
boardMain[row][col] = '.'; // 回溯
}
}
}
// 获取递归传入的行数和列数
public int[] handler(int row,int col){
int[] r = new int[2];
if (col==8) {
row++;
col = 0;
}else{
col++;
}
r[0] = row;
r[1] = col;
return r;
}
// 判断该 位置 是否可以放置
public boolean isVaild(int row,int col,int n){
// 处理行
char[] currentRow = boardMain[row];
char nc = (char)(n+'0');
for (char c : currentRow) {
if (c==nc) {
return false;
}
}
// 处理列
for(int i=0;i<9;i++){
char c = boardMain[i][col];
if (c==nc) {
return false;
}
}
// 处理九宫格
int ar = (int)Math.ceil((row+1)/3.0);
int ac = (int)Math.ceil((col+1)/3.0);
int startRow = (ar-1)*3;
int startCol = (ac-1)*3;
for(int i=startRow;i<startRow+3;i++){
for(int j=startCol;j<startCol+3;j++){
if (boardMain[i][j]==nc) {
return false;
}
}
}
return true;
}
}

 回溯法是一种纯暴力的搜索,并不是一种高效的算法。
回溯法是一种纯暴力的搜索,并不是一种高效的算法。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号