sqrt开平方算法解析

昨天笔试遇到一题，要求用java实现sqrt，当时就想，哪里管过怎么实现的，都是直接拿来用的。所以晚上就查了一些资料，将实现过程整理如下：

图示：

 

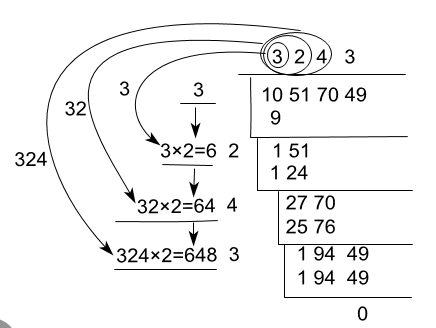
算法思路（说明，下面的“碎片被开方数”，“补丁平方根”是为了方便称呼自取的名称）：

• 1.将被开方数n从右向左两位一划分，例如将10517049划分为10 51 70 49（可能是因为n的平方根肯定是n位数的一半吧，没找到解释的相关资料）；
• 2.获取“碎片被开方数”fragmentSqrt。从左向右每次取划分好的两位数，fragmentSqrt在第一次取值时就是n的最高一组两位数（这里是10），此后就是第4步计算的余数remainder和取到的两位数拼接（例如1 51，27 70，194 49）；
• 3.推测fragmentSqrt的“补丁平方根”patchRoot的个位bit_patchRoot；

          推测公式为(high_patchRoot×2×10+bit_patchRoot)×bit_patchRoot，使其尽可能小于等于fragmentSqrt，循环bit_patchRoot从9~1即可。high_patchRoot为上一轮的补丁平方根”patchRoot。

          推测公式的解释：以1156为例，易观察到它的平方根是两位，十位是3，设个位是a，则（3×10+a）²=1156，即30²+2×3×10a+a²=1156，即3×2×10a+a²=256，3×2×10a+a²变形为（3×2×10+a）a，即为推测公式。故2为（x+y）²=x²+2xy+y²中的2，×10表示是十位数。

• 4.计算余数remainder；

           remainder=fragmentSqrt-(high_patchRoot×2×10+bit_patchRoot)×bit_patchRoot

• 5.更正“补丁平方根”patchRoot；

           patchRoot=high_patchRoot×10+bit_patchRoot

• 6.返回第二步

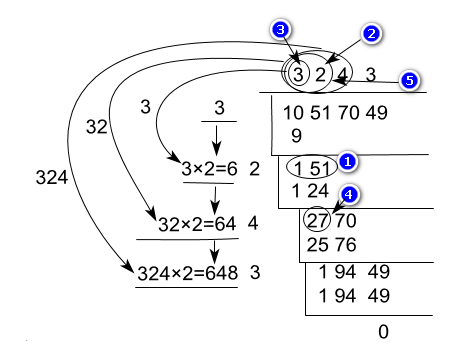
①151为“碎片被开方数”fragmentSqrt

②2为bit_patchRoot

③3为high_patchRoot，即上一轮的patchRoot

④27为余数remainder

⑤32位patchRoot

①~⑤是第二轮结果

 代码

 

package kafka.productor;

import java.math.BigInteger;
import java.util.Scanner;

public class MySqrt {
	static final BigInteger NUM20 = BigInteger.valueOf(20);// 将后面使用的参数定义为final常量
	
	public static void main(String[] args) {
		MySqrt mySqrt = new MySqrt();
		Scanner input = new Scanner(System.in);
		System.out.println(mySqrt.sqrt(input.next()));
	}
	
	public String sqrt(String n){
		String patchRoot="0";   // 平方根初始化为字符串0
		String remainder="";    //余数初始化为""
		if(n.length()%2 != 0) n = "0"+n; //如果n是奇数为，防止substring越界
		for(int i=0; i<n.length()/2; i++){//两两分组
			String fragmentSqrt = remainder+n.substring(2*i,2*i+2); //第2步
			String high_patchRoot = patchRoot;
			String bit = getBit(new BigInteger(high_patchRoot),new BigInteger(fragmentSqrt));  //第3步
			remainder = getRemainder(new BigInteger(fragmentSqrt),new BigInteger(high_patchRoot),new BigInteger(bit));  //第4步
			patchRoot = high_patchRoot+bit;  //第5步
		}
		return patchRoot.substring(1); // 去掉结果之前的0
	}

	private String getRemainder(BigInteger fragmentSqrt, BigInteger high_patchRoot, BigInteger bit_patchRoot) {
	    return fragmentSqrt.subtract(high_patchRoot.multiply(NUM20).add(bit_patchRoot).multiply(bit_patchRoot)).toString();
	}

	private String getBit(BigInteger high_patchRoot,BigInteger fragmentSqrt) {
		int i;
		for(i=9; i>0; i--){
			BigInteger bi = BigInteger.valueOf(i);
			if (fragmentSqrt.compareTo(high_patchRoot.multiply(NUM20).add(bi).multiply(bi))>=0) 
				break;
		}
		return String.valueOf(i);
	}
}

 参考

https://blog.csdn.net/Super2333/article/details/79476149

https://baike.baidu.com/item/%E5%BC%80%E5%B9%B3%E6%96%B9%E8%BF%90%E7%AE%97/1165387?fr=aladdin

为了得到而努力

2019-03-07

转载请注明来处。