五、树和二叉树

(待完善)

 基本概念：

树（Tree）：

　　是n（n>=0）个结点的有限集T,T为空时称为空树，否则满足如下两个条件：

（1）有且仅有一个特定的称为根（Root）的结点；

（2）其余结点可分为m（m>=0）个互不相交的子集，其每个子集又是一棵树，并称其为根的子树（Subtree）。

树中的结点拥有的子树称为该结点的度（Degree）。

度为零的结点称为叶子（Leaf）或 终端结点。

树中结点的最大层数称为树的高度（Height） 或 深度（Depth）。

森林 ：

　　是（m>=0）棵互不相交的树的集合。（树个森林的概念相近。删去一棵树的根，就得到了一个森林；反之，加上一个结点作为树根，森林就变成了一棵树。）

二叉树（BinaryTree）：

　　由一个根结点及两棵互不相交的称作这个根的左子树和右子树的树组成。

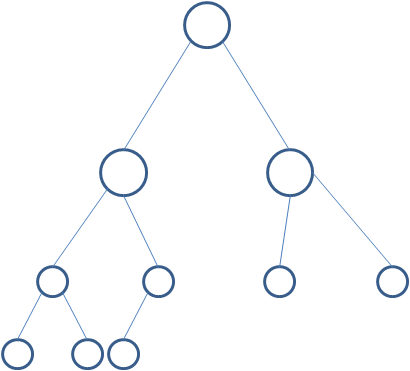
完全二叉树：

　　一棵二叉树至多最下面的两层上的结点可以小于2，并且最下一层结点都集中在左边位置。（最后一层可以不完全填充，其叶子结点都靠左对齐。）

 

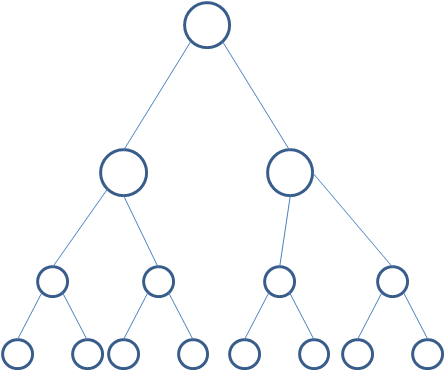
满二叉树（完美二叉树）：

　　深度为k且有2^k-1个结点的二叉树。（每一层(包含最后一层)都被完全填充。满二叉树是完全二叉树。）

---

树的遍历

（二维的树转变为一维的线性表）

 

遍历的应用

　　查找树的叶子节点

　　求树高度（深度）

　　运算表达示树

　　利用遍历序列确定树

 

二插搜索树

　　搜索树的查找

　　搜索树的插入

　　搜索树的删除

 

集合

 

树，二叉树，森林的相互转换

1. 将树转换为二叉树：

   树中每个结点最多只有一个最左边的孩子(长子)和一个右邻的兄弟。按照这种关系很自然地就能将树转换成相应的二叉树：1.在所有兄弟结点之间加一连线2.对每个结点，除了保留与其长子的连线外，去掉该结点与其它孩子的连线。

   如下图所示：

   
2. 2

   将一个森林转换为二叉树：

   具体方法是：1.将森林中的每棵树变为二叉树；2.因为转换所得的二叉树的根结点的右子树均为空，故可将各二叉树的根结点视为兄弟从左至右连在一起，就形成了一棵二叉树。

   如下图所示：

   
3. 3

   二叉树转换为树：

   是树转换为二叉树的逆过程。

   1.加线。若某结点X的左孩子结点存在，则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点…，都作为结点X的孩子。将结点X与这些右孩子结点用线连接起来。

   2.去线。删除原二叉树中所有结点与其右孩子结点的连线。

   如下图所示：

   
4. 4

   二叉树转换为森林：

   假如一棵二叉树的根节点有右孩子，则这棵二叉树能够转换为森林，否则将转换为一棵树。

   1.从根节点开始，若右孩子存在，则把与右孩子结点的连线删除。再查看分离后的二叉树，若其根节点的右孩子存在，则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。

   2.将每棵分离后的二叉树转换为树。

   如下图所示：

   

5.