四、串、数组和广义表

(内容待完善)

知识点

串的模式匹配又称子串定位运算或串匹配。在匹配中，将主串称为目标（串），子串称为模式（串）。

BF法(Brute Force):

KMP法:

---

串的模式匹配的两种方法。BF法,朴素的串匹配法。KMP法，尽可能的滑动得更远，利用部分的匹配结果。

朴素的模式匹配算法（BF算法）

图示说明

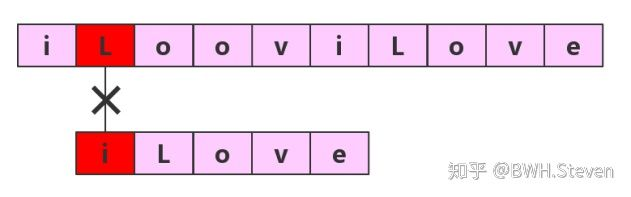
第一轮比较：

 

第二轮比较：

 

 

...... 原理一致，省略中间步骤

第五轮：

 

 

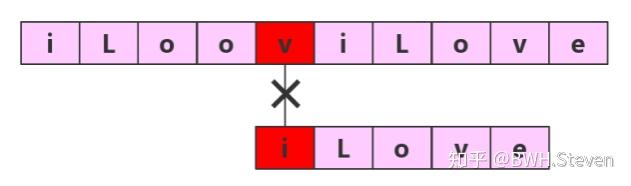
第六轮：

 

 

• 第一轮：子串中的第一个字符与主串中的第一个字符进行比较
• 若相等，则继续比较主串与子串的第二个字符
• 若不相等，进行第二轮比较

• 第二轮：子串中的第一个字符与主串中第二个字符进行比较......
• 第N轮：依次比较下去，直到全部匹配
  
  

代码实现:

(略)

 

BF算法优点：思想简单，直接，缺点：每次字符不匹配时，都要回溯到开始位置，时间开销大。时间复杂度 O((n-m+1)*m) 。

 

KMP模式匹配算法

图示说明:

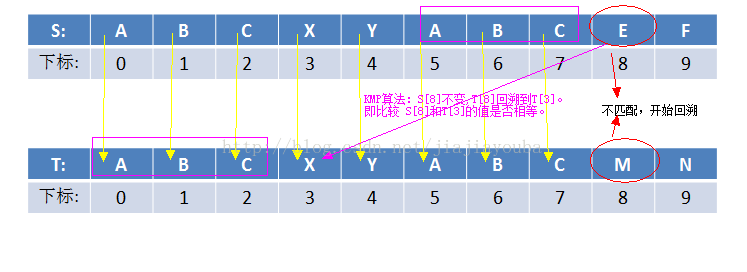
从图中，我们可以很容易的发现，因为前面的字符,S和T中存在同的元素,所以S不必回溯到S[1]的位置，T也不必回溯到T[0]的位置。我们就可直接跳过对相同元素的回溯比较，直接比较S[8]与T[3]。

因此我们构建一个next数组储存回溯位置。

 

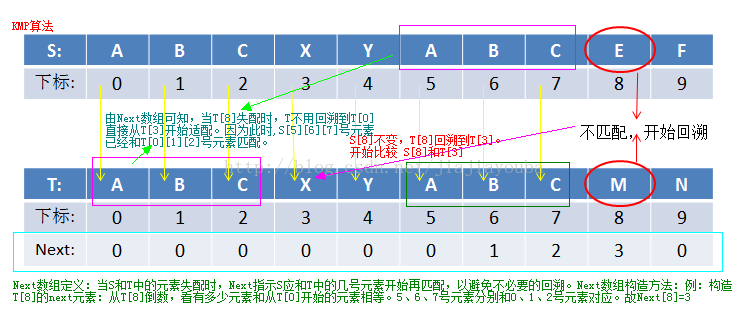
KMP算法的思想：假设在模式匹配的进程中，执行T[i]和W[j]的匹配检查。若T[i]=W[j]，则继续检查T[i+1]和W[j+1]是否匹配。

next数组两种求法

（1）第一种求法：根据前一个字符的next值求

初始化:

 

 

 

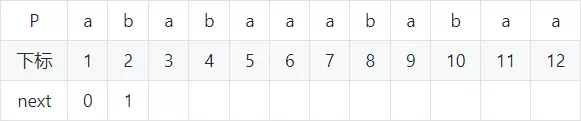
代码实现：

 1 char t[]={"ababaabab"};
 2 int Len=strlen(t);
 3     
 4     int i = 0, j = -1;
 5     int next[len];
 6     next[0]=-1;
 7      while (i < len - 1) {
 8          if ((j == -1) || t[i] == t[j]) {
 9              ++i, ++j;
10              next[i] = j;
11          }else{
12              j = next[j];
13          }
14      }
15 
16     for(i=0;i<len;i++)
17     {printf("next[%d]->%d\n",i,next[i])}

 

 

 

 

（2）第二种求法：根据最大公共元素长度求

 

 

 

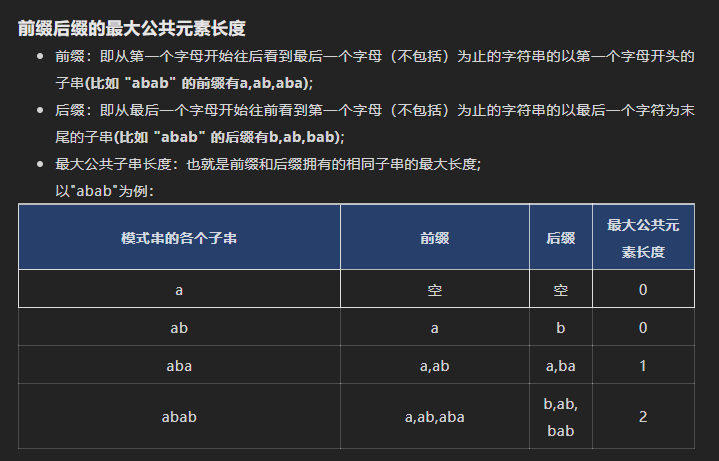
next数组优化（nextval的求法）

当子串中有多个连续重复的元素，例如主串 S=“aaabcde” 子串T=“aaaaax” 在主串指针不动，移动子串指针比较这些值，其实有很多无用功，因为子串中5个元素都是相同的a，所以我们可以省略掉这些重复的步骤。

nextval其实是next的改进。