SVD 及其应用

线性代数基础

酉矩阵（unitary matrix）是一种特殊的方阵，它满足 \(UU^T=U^TU=I_n\).

不难看出，酉矩阵实际上是推广的正交矩阵（orthogonal matrix）；当酉矩阵中的元素均为实数时，酉矩阵实际就是正交矩阵。

SVD(Singular Value Decomposition)-万能矩阵分解

是特征分解的广义化,能够分解任意维数的矩阵,而特征分解只针对于方阵. MATLAB 与 scipy.linalg 中有直接计算的函数\([U\ \Sigma\ V]=svd(A)\). 其中\(\Sigma_i\)称为奇异值,是正数.

任何秩为r的矩阵$ A \in \mathbb R_{m×n}$ ,可以被分解为

\[\begin{align} A & =\underbrace{[U_1U_2]}_U \underbrace{\begin{bmatrix} \Sigma_1 & 0_{r\times(n-r)} \\ 0_{(m-r)\times r } & 0_{(m-r)\times (n-r) } \end{bmatrix} }_\Sigma \underbrace{\begin{bmatrix} V_1^T \\ V_2^T \end{bmatrix} }_{V^T} \\ & =U\Sigma V^T \tag 1\\ & =U_1\Sigma_1 V_1^T \tag 2\\ & =\sum_{i=1}^r \sigma_i u_i v_i^T \tag 3 \end{align} \]

其中U和V\(\in\mathbb R^{m\times m}\)是正交矩阵.式(1)便于分析,但并不计算有效;(2)计算有效,但有时不方便分析;(3)方便展开,用于低秩矩阵计算。

下图可以很形象的看出上面SVD的定义：

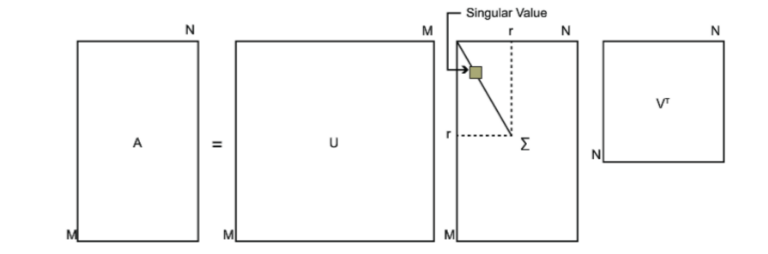
接下来求解U,Σ,V 这三个矩阵.

矩阵A是 \(m×n\) 的矩形阵, 而 \(A^TA\) 是 \(n×n\) 的方阵, \(AA^T\) 是 \(m×m\) 的方阵. 可以对方阵进行特征分解:

\[(A^TA)v_i = \lambda_i v_i \\ (AA^T)u_i = \lambda_i u_i \]

那么我们是否可以将特征分解的结果当作SVD分解中的U,V呢?
是可以的,

\[A=U\Sigma V^T \\ \Rightarrow A^T=V\Sigma^T U^T \\ A^TA = V\Sigma^T U^TU\Sigma V^T = V\Sigma^2V^T \\ AA^T = U\Sigma V^T V\Sigma^T U^T = U\Sigma^2U^T \]

可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：

\[σ_i=\sqrt {λ_i} \]

奇异值分解意义

奇异值往往对应着矩阵中隐含的重要信息，且重要性和奇异值大小正相关。每个矩阵都可以表示为一系列秩为1的“小矩阵”之和，而奇异值则衡量了这些“小矩阵”对应的权重。

在图像处理领域，奇异值不仅可以应用在数据压缩上，还可以对图像去噪。如果一副图像包含噪声，我们有理由相信那些较小的奇异值就是由于噪声引起的。当我们强行令这些较小的奇异值为0时，就可以去除图片中的噪声。

奇异值分解还广泛的用于主成分分析（PCA）和推荐系统等。在这些应用领域，奇异值也有相应的意义。

降维

\[A_{m \times n} = U_{m \times m}\Sigma_{m \times n} V^T_{n \times n} \approx U_{m \times k}\Sigma_{k \times k} V^T_{k \times n} \]

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。

右奇异矩阵可以用于列的降维即特征维度的压缩(如PCA)，左奇异矩阵可以用于行数的压缩(去相关)。

SVD 用于 PCA

PCA降维，需要找到样本协方差矩阵\(X^TX\)的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，PCA仅仅使用了我们SVD的右奇异矩阵。当样本数多样本特征数也多的时候，协方差矩阵的计算量是很大的。

有一些SVD的实现算法可以不求先求出协方差矩阵，也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是特征分解。

因为PCA需要进行去均值化处理，所以不可避免的破坏了矩阵的稀疏性。所以，对于稀疏矩阵来说，SVD更适用，这样对于大数据来说节省了很大空间。

优缺点

优点: SVD可以实现并行化
缺点: 分解出的矩阵解释性不强

因此对全连接层的权重参数进行压缩，可在不显著降低性能的情况下减少训练时间和降低模型的存储空间。

SVD 应用之全连接层压缩

SVD分解的一般形式是 \(A_{m\times n}\approx U_{m\times k}\sum_{k\times k}V_{k\times k}^T=U_{m\times k}N_{k\times k}\).

将全连接层的权重视作\(A_{m\times n}\), 可以被压缩成另一种分解形式: \(A_{m\times n}\approx U_{m\times c}N_{c\times n}\).
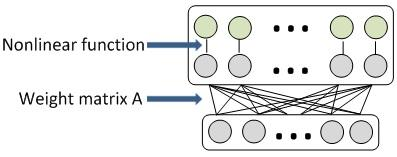
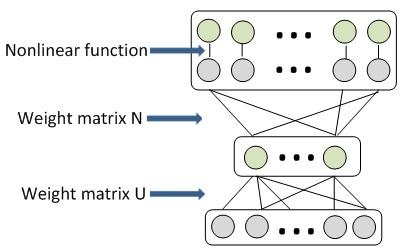
基于奇异值分解(SVD)的全连接层压缩方法就是引入一个中间层L’,该中间层包含c个神经元, 在c较小时可以减少连接数和权重规模,权重矩阵规模从 mn减少到(m+n)c,从而降低运行深度模型的计算和存储需求.

原始DNN模型(1层全连接层)与权重压缩(添加新层)之后的新模型:

SVD 的实现

svd的经典算法有Golub-Kahan算法、分治法、Jacobi法几种. 也有随机化的版本RedSVD等.

参考:

• 奇异值分解(SVD)原理与在降维中的应用
• 谈谈矩阵的 SVD 分解