Deformable ConvNets
Deformable ConvNets
论文 Deformable Convolutional Networks(arXiv:1703.06211)
CNN受限于空间结构,具有较差的旋转不变性,较弱的平移不变性.这篇论文提出了两个可替换原有组件的模块:可变形卷积和RoI pooling.均基于增加空间采样位置,通过网络学习位置偏移的思想.
传统增加空间变换性的方法
-
数据集增广
通过仿射变换等使数据集具有足够多的变换形式,使得模型能够从数据中学习到鲁棒的表示.但缺点是训练代价大,模型参数复杂.
-
使用具有一定空间不变性的特征和算法
如SIFT特征和基于滑窗的目标检测方法.
上述方法均需要利用一定的先验知识,不具有广泛的通用性.
Deformable Convolution
通过变换标准的卷积中的采样网格使得采样的位置是自由的形状,而不拘束于传统的矩形,其实现方式是通过额外的并列的卷积层学习位置偏移,仅增加了少量的参数来学习偏移.后边的讨论均以2-D卷积为例.
在普通卷积中每个像素点的计算方式为:
如3x3卷积,dilation=1的9个位置为\(\mathcal R=\{(-1,-1),(-1,0),\cdots,(0,1),(1,1)\}\),对输出特征图上的每个位置\(p_0\),有:
在可变卷积中引入偏移量\(\Delta p_n\)使得采样位置不规则,公式变为:
由于\(\Delta p_n\)很小,上式中的采样点会是浮点型, \(x(p_0+p_n+\Delta p_n)\)可以通过双线性差值得到:
其中\(p=p_0+p_n+\Delta p_n\)代表任意的位置,q遍历特征图x上的所有空间位置(其实仅利用了插值点p的相邻元素),G是bilinear interpolation kernel,且是2-D的: \(G(q, p) = g(q_x , p_x ) · g(q_y , p_y )\),其中\(g(a, b) = \max(0, 1 − |a − b|)\).
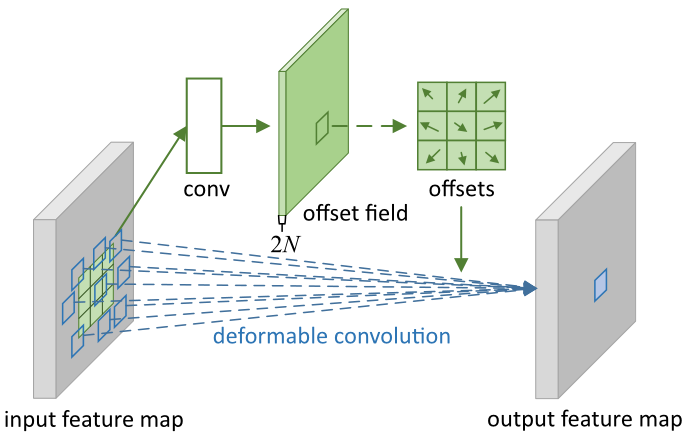
值的注意的是deformable conv学习的是输出特征图上每个特征点对应输入特征图上的卷积作用位置的偏移量, 而deformable conv的kernel中并非偏移量(conv之后的特征图才是偏移量).
上图中offset field和input feature map的尺寸大小相同, 通道数是输入特征图通道的两倍, 因为偏移量需要用(x,y)两个维度表示. 这个额外的产生偏移量的conv/fc层的权重初始化为0.
论文中提到了以下几个分割和检测网络,在其上运用可变形卷积:
- DeepLab 是一个语义分割网络,在特征图上使用1x1的卷积产生C+1个图表示每个像素的分类score,再接softmax得到概率值.
- 多类别RPN(Category-Aware region proposal network),将faster rcnn中提出的RPN的2类别(目标/非目标)替换为C+1个类别.可以被认为是简化版的SSD.
- Faster R-CNN在此论文中采用了FPN的设计方式将RoIPooling添加到最后的卷积层之后来减少每个RoI的计算量.RoI pooling 层可以被替换为deformable RoI pooling.
- R-FCN具有可以忽略的per-ROI计算代价.RoI pooling 可以被 deformable position-sensitive RoI pooling替换.
与 STN 的对比
STN 是最早的一篇在网络中学习空间变换的论文工作, 但是仿射变换的代价很大, 学习这样的参数比较困难. 在小尺寸的图像分类任务中运用的较好. (随后有STN的改进: inverse STN).
Deformable convolution可以看作是STN的轻量级版本,但是并不采用STN的特征变换方式.
Deformable convolution可以很容易的集成到任何CNN结构中,它的训练简单,对于复杂的任务比较有效,如稠密预测(语义分割),半稠密预测(目标检测),而这些任务对于具有相似思想的STN(空间变换网络)则较难.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号