摄像机P矩阵生成与转换

 

一、针孔模型：

　　

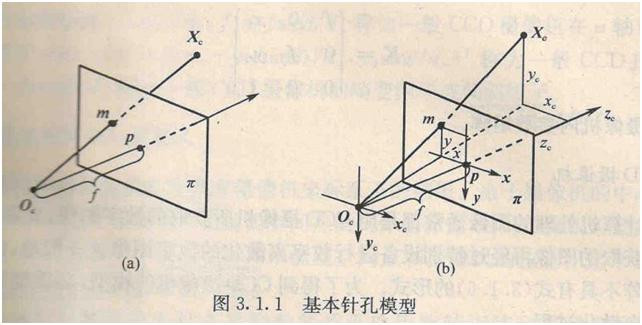
　　其中π为摄像机的像平面，Oc为摄像机中心（或光心），f是摄像机的焦距，OP为光轴（或主轴）端点Oc垂直于像平面的射线，主轴与像平面的焦点P是摄像机的主点。

　　如b图所示，图像坐标系为P-xy，摄像机坐标系为Oc-xcyczc，记空间点Xc在摄像机坐标系中的齐次坐标为：

　　　　　　　　　                                　

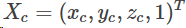
 　　 它的像点m在图像坐标系中的齐次坐标记为：

　　　　　　　　　　　　　　　　　　　

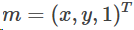
　　  根据三角形相似原理，可知：

　　　　　　　　　　　　　　　　　　　　　　　　

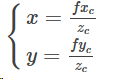
　　即：

　　　　　　　　　　　　　　　　　　

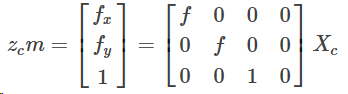
二、主点偏离图像中心

　　上面讨论的是理论的情况下，但是在实际情况下，主点可能不是图像坐标系原点（图像坐标系中心），因为他们会有一定的的偏移量。若主点在图像坐标系中的坐标（即偏移量为（x0，y0））：

　　　　　　　　　　　　　　　　　　　

 

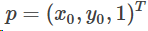
　　即（内参矩阵K）：

　　　　　　　　　　　　　　　　　　　

 

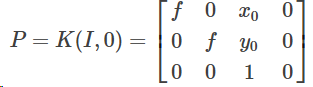
三、CCD摄像机

　　1、数字离散化

　　 　　我们通常获取到的图像是CCD摄像机采集的数字图像，CCD相机是将图像平面的点进行数字离散化。离散化之后的像素是一个矩形，矩形的长宽分别为dx，dy，则像素的坐标为，即：

　　　　　　　　　　　　　　　　　　　　

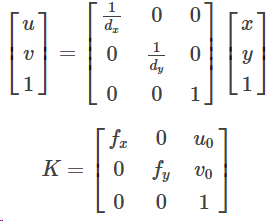
　　　　为CCD的内参数矩阵，其中fx=f/dx，fy=f/dy称为CCD摄像机在u轴和v轴方向上的尺度因子，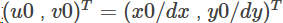

为CCD摄像机的主点。

　　2、倾斜因子

　　　　由于工艺，CCD存在一个倾斜因子s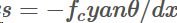，。所以更一般的表示为：

　　　　　　　　　　　　　　　　　　

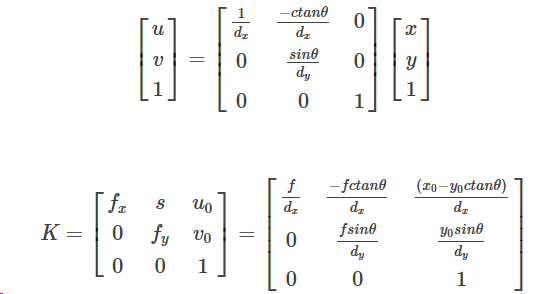
四、外参数矩阵

　　我们一般在描述一个三维点的时候，由于相机可能一直在运动，所以我们并不是基于摄像机坐标系下对其描述，我们通常是在世界坐标系下进行描述。而世界坐标系与相机坐标系之间的关系可以用旋转矩阵和平移向量来描述（3x3的旋转矩阵R和3x1的位移向量T）。

　　旋转矩阵R：在三维空间中，旋转可以分解为绕各自坐标轴的二维旋转，其中旋转轴线的度量保持不变。如果依次绕x，y，z轴旋转，那么总的旋转矩阵R是三个矩阵的乘积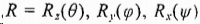，其中：

　　　　　　　　　　

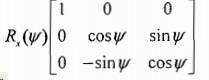
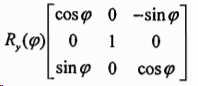
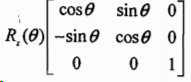
　　平移向量T：摄像机坐标系下世界坐标系原点的位置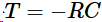，其中C是摄像机在世界坐标系中的位置。

　　所以摄像机矩阵P可以表示为：

　　　　　　　　　　

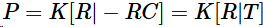
五、总的转换关系

  　　　　　　　　　　　　

 

 

 

 

 

 

参考：

https://blog.csdn.net/u010128736/article/details/52850444/

http://haiyangxu.github.io/posts/2014/2014-06-12-camera-matrix.html

https://blog.csdn.net/yangdashi888/article/details/51356385

 

 OOOc