随便记录下
湖南省第十八届大学生计算机程序设计竞赛(HNCPC2022)
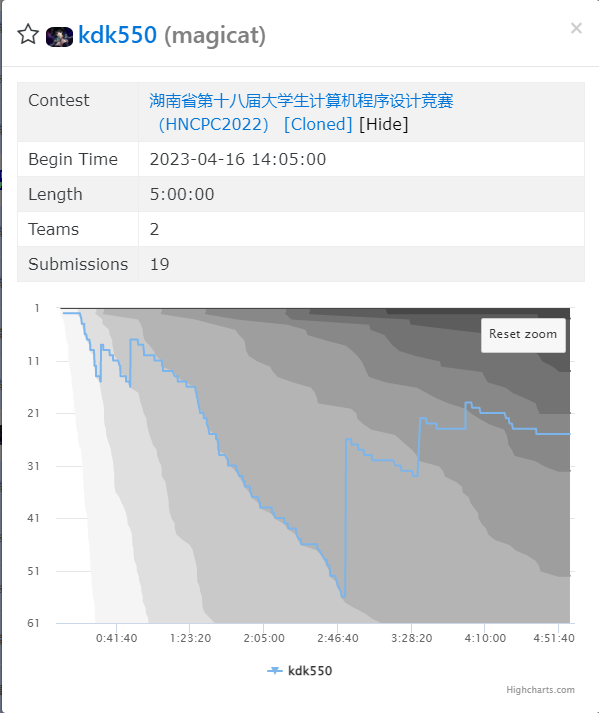
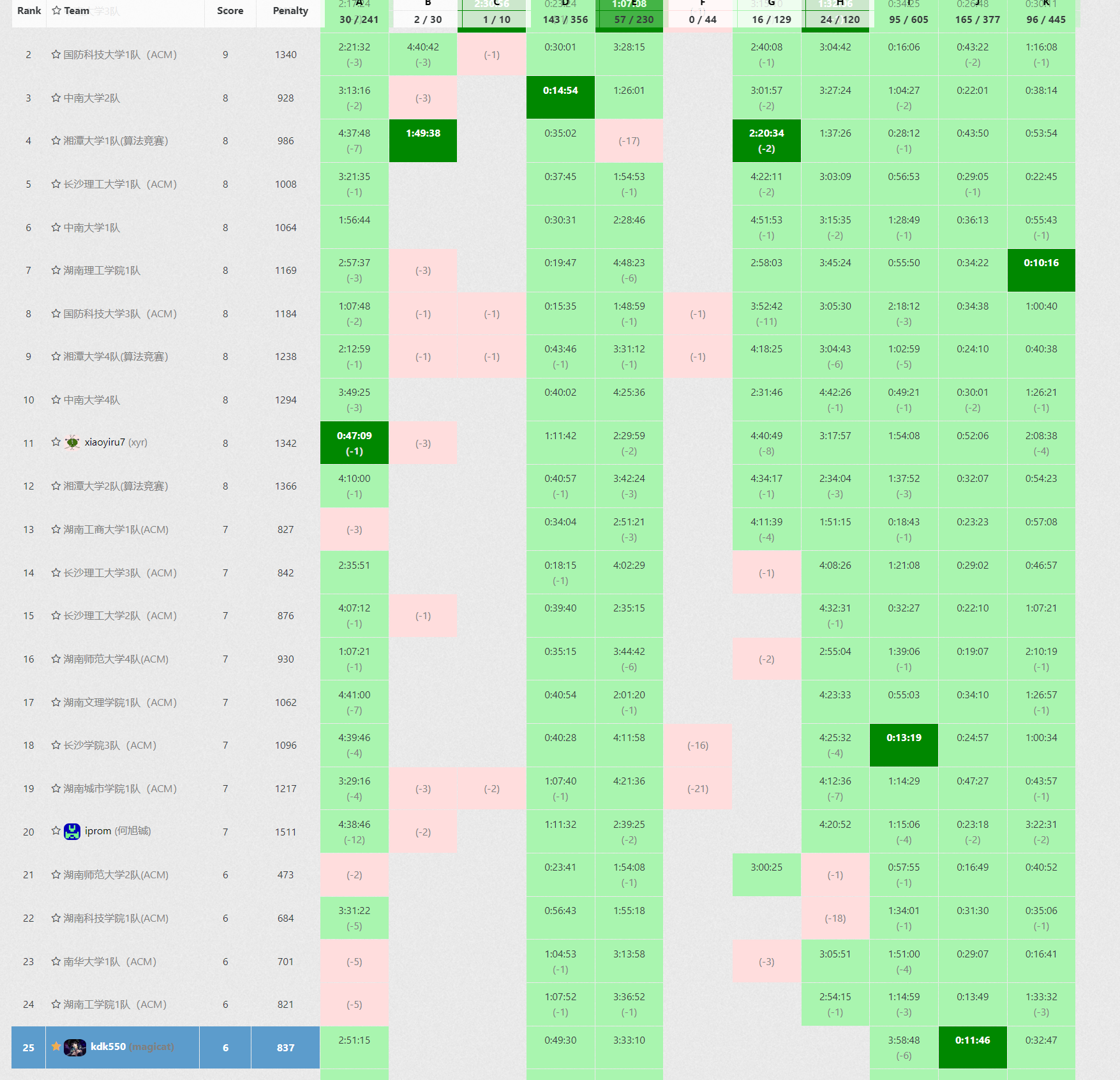
VP情况
队友卡I占了机时导致罚时有点爆炸,也是策略的失误
6题837罚时
补到GH就不补个位数题
J
判断斐波那契区间有没有一段的和等于\(n\)
由于\(n \leq 10^{15}\)直接暴力即可
#include<bits/stdc++.h>
using namespace std;
long long f[110];
int cnt;
void init()
{
f[1] = 1, f[2] = 1;
cnt = 2;
while(f[cnt] <= 1e15)
{
f[cnt + 1] = f[cnt] + f[cnt - 1];
cnt++;
}
}
int main()
{
init();
long long n;
while(cin>>n)
{
bool ok = false;
for(int i = 1; i <= cnt; i++)
{
long long sum = 0;
for(int j = i; j <= cnt; j++)
{
sum += f[j];
if(sum == n)
{
ok = true;
}
else if(sum > n)
break;
}
}
if(ok)
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
}
K
判断字符串有没有不是前缀的字串与字符串的前缀相等,打印所有符合条件的字串长度
队友告诉我这是kmp的性质,但我忘记kmp是什么了,直接双hash + 二分过了,枚举字串起点,二分满足条件的字串长度
// AC one more times
#include <bits/stdc++.h>
using namespace std;
#define int long long
typedef pair<int, int> PII;
struct DoubleStringHash
{
// #define int long long
vector<int> h1, h2, w1, w2;
int base1 = 131, base2 = 13331;
int p1 = 1e9+7, p2 = 1e9+9;
void init(string s) {
int len = s.size();
s = " " + s;
h1.resize(len + 1), w1.resize(len + 1);
h2.resize(len + 1), w2.resize(len + 1);
h1[0] = 0, w1[0] = 1;
h2[0] = 0, w2[0] = 1;
for(int i = 1; i <= len; i++) {
h1[i] = (h1[i - 1] * base1 + s[i]) % p1, w1[i] = w1[i-1] * base1 % p1;
h2[i] = (h2[i - 1] * base2 + s[i]) % p2, w2[i] = w2[i-1] * base2 % p2;
}
}
pair<int, int> get(int l, int r) {
return {(h1[r] - h1[l - 1] * w1[r - l + 1] % p1 + p1) % p1, (h2[r] - h2[l - 1] * w2[r - l + 1] % p2 + p2) % p2};
}
}ha;
bool cmp(string a, string b) {
return a.size()<b.size();
}
string s;
void solve()
{
int n = s.size();
ha.init(s);
s = "?" + s;
long long ans = 0;
for(int i = 2; i <= n; i++)
{
if(s[i] == s[1])
{
int l = 1, r = n - i + 1;
while(l < r)
{
int mid = (l + r + 1) >> 1;
//cout<<i <<" "<<i + mid - 1<<" "<<1<<" "<<mid<<endl;
if(ha.get(i, i + mid - 1) == ha.get(1, mid))
l = mid;
else r = mid - 1;
}
//cout<<i<<" " <<l <<endl;
int t = l;
ans += (t * t + t) / 2ll;
}
}
cout<<ans<<endl;
return;
}
signed main()
{
std::ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
while(cin>>s)
{
//cout << "Case #" << tc << ": ";
solve();
}
return 0;
}
D
矩阵乘法,但直接做会T,队友手推了一下式子发现,\(A\)和\(B\)矩阵的元素是一行或一列地去用,但具体观察到的式子留在了我队友的草稿纸上,手推一下也不难,大学生应该都写过线代了吧
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
int n;
ll a1,a2,b1,b2;
int A[1010][1010];
int B[1010][1010];
int ca[1010];
int rb[1010];
const int mod = 1e9 + 7;
void solve()
{
memset(ca, 0 ,sizeof ca);
memset(rb, 0 ,sizeof rb);
cin>>a1>>a2>>b1>>b2;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
{
A[i][j] = (i - 1) * a1 + (j - 1) * a2;
B[i][j] = (i - 1) * b1 + (j - 1) * b2;
}
for(int j = 1; j <= n; j++)
{
for(int i = 1; i <= n; i++)
{
ca[j] += A[i][j];
ca[j] %= mod;
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
rb[i] += B[i][j];
rb[i] %= mod;
}
}
int ans = 0;
for(int i = 1; i <= n; i++)
{
ans += (ca[i] * rb[i]);
ans %= mod;
}
cout<<ans<<endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
int t = 1;
//cin>>t;
while(cin>>n)
{
solve();
}
return 0;
}
A
队友告知我这题要维护树上区间修改,树上区间查询最小值,一样树链剖分 + 线段树的裸题,直接改改板子
// AC one more times
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define endl '\n'
#define all(x) (x).begin(), (x).end()
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<long long,long long> PLL;
const int N = 4e4 + 10;
vector<PII> e[N];
int n, q;
int tot, l[N], r[N], tid[N], top[N], bs[N], sz[N], f[N], dep[N];
LL w[N];
PII edge[N];
void dfs1(int u, int fa)
{
sz[u] = 1;
dep[u] = dep[fa] + 1;
bs[u] = -1;
f[u] = fa;
for(auto v : e[u])
{
if(v.fi == fa) continue;
dfs1(v.fi, u);
w[v.fi] = v.se;
sz[u] +=sz[v.fi];
if(bs[u] == -1 || sz[v.fi] > sz[bs[u]])
bs[u] = v.fi;
}
}
void dfs2(int u,int t)
{
l[u] = ++tot;
tid[tot] = u;
top[u] = t;
if(bs[u] != -1)
dfs2(bs[u], t);
for(auto v : e[u])
{
if(v.fi == bs[u] || v.fi == f[u]) continue;
dfs2(v.fi, v.fi);
}
r[u] = tot;
}
struct info
{
int miv;
};
info operator + (const info &a, const info &b)
{
return (info){min(a.miv, b.miv)};
}
struct segtree
{
struct info val;
int tag;
}seg[N * 4];
void update(int id)
{
seg[id].val = seg[id * 2].val + seg[id * 2 + 1].val;
}
void settag(int id, int tag)
{
seg[id].tag += tag;
seg[id].val.miv = seg[id].val.miv + tag;
}
void pushdown(int id)
{
if(seg[id].tag != 0)
{
settag(id * 2, seg[id].tag);
settag(id * 2 + 1, seg[id].tag);
seg[id].tag = 0;
}
}
void build(int id, int l, int r)
{
seg[id].tag = 0;
seg[id].val.miv = 10000000;
if(l == r)
{
seg[id].val = {w[tid[l]]};
//cout<<seg[id].val.miv<<endl;
return;
}
int mid = (l + r) >> 1;
build(id * 2, l, mid);
build(id * 2 + 1, mid + 1, r);
update(id);
}
void modify(int id, int l, int r, int ql, int qr, int tag)
{
if(ql > qr || l > r) return;
if(l == ql && r == qr)
{
settag(id, tag);
return;
}
pushdown(id);
int mid = (l + r) >> 1;
if(qr <= mid)
modify(id * 2, l, mid, ql, qr, tag);
else if(ql > mid)
modify(id * 2 + 1, mid + 1, r, ql, qr, tag);
else
{
modify(id * 2, l, mid, ql, mid, tag);
modify(id * 2 + 1, mid + 1, r, mid + 1, qr, tag);
}
update(id);
}
info query(int id, int l, int r, int ql, int qr)
{
if((ql > qr || l > r)) return (info){100000000};
if(l == ql && r == qr)
{
return seg[id].val;
}
pushdown(id);
int mid = (l + r) >> 1;
if(qr <= mid)
return query(id * 2, l, mid, ql, qr);
else if(ql > mid)
return query(id * 2 + 1, mid + 1, r, ql, qr);
else
{
return query(id * 2, l, mid, ql, mid) +
query(id * 2 + 1, mid + 1, r, mid + 1, qr);
}
update(id);
}
void modify(int u, int v, int k)
{
while(top[u] != top[v])
{
if(dep[top[u]] > dep[top[v]])
{
modify(1, 1, n, l[top[u]], l[u], k);
//cout<<query(1, 1, n, l[top[u]], l[u]).miv<<endl;
u = f[top[u]];
}
else
{
modify(1, 1, n, l[top[v]], l[v], k);
//cout<<query(1, 1, n, l[top[v]], l[v]).miv<<endl;
v = f[top[v]];
}
}
if(dep[u] < dep[v]) swap(u, v);
modify(1, 1, n, l[v] + 1, l[u], k);
//cout<<query(1, 1, n, l[v] + 1, l[u]).miv<<endl;
}
info query(int u, int v)
{
info ans = (info){100000000};
while(top[u] != top[v])
{
if(dep[top[u]] > dep[top[v]])
{
ans = ans + query(1, 1, n, l[top[u]], l[u]);
u = f[top[u]];
}
else
{
ans = ans + query(1, 1, n, l[top[v]], l[v]);
v = f[top[v]];
}
//cout<<ans.miv<<endl;
}
if(dep[u] < dep[v]) swap(u, v);
ans = ans + query(1, 1, n, l[v] + 1, l[u]);
// cout<<ans.miv<<endl;
return ans;
}
void init()
{
tot = 0;
for(int i = 1; i <= n; i++)
{
e[i].clear();
l[i] = 0;
r[i] = 0;
tid[i] = 0;
top[i] = 0;
bs[i] = 0;
sz[i] = 0;
f[i] = 0;
dep[i] = 0;
w[i] = 0;
edge[i] = {0, 0};
}
for(int i = 1; i <= 4 * n; i++)
{
seg[i].tag = 0;
seg[i].val.miv = 1000000;
}
}
void solve()
{
/*
vector<PII> e[N];
int n, q;
int tot, l[N], r[N], tid[N], top[N],
bs[N], sz[N], f[N], dep[N];
LL w[N];
PII edge[N];
*/
/*
5 2
1 2 5
3 1 2
4 3 4
5 3 3
4 2 1
5 2 2
5 2
1 2 5
3 1 2
4 3 4
5 3 3
4 2 1
5 2 2
*/
init();
cin>>q;
for(int i = 1; i < n; i++)
{
int u, v, w; cin>>u>>v>>w;
edge[i] = {u, v};
e[u].pb({v, w});
e[v].pb({u, w});
}
dfs1(1, 0);
dfs2(1, 1);
build(1, 1, n);
int ans = 0;
/*
cout<<"L: "<<endl;
for(int i = 1; i <= n; i++)
cout<<i <<" L: "<<l[i]<<endl;
cout<<"R: "<<endl;
for(int i = 1; i <= n; i++)
cout<<i <<" R: "<<r[i]<<endl;
*/
for(int i = 1; i <= q; i++)
{
int u, v, w; cin>>u>>v>>w;
info t = query(u, v);
//cout<<"-----------\n";
if(t.miv < w)
continue;
else
{
modify(u ,v, -w);
ans += w;
}
//cout<<"QUERY: "<<i<<" "<<t.miv<<endl;
//cout<<"TREE: "<<endl;
}
cout<<ans<<endl;
return;
}
int main()
{
std::ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int TC = 1;
//cin >> TC;
while(cin>>n)
{
solve();
}
return 0;
}
E
小模拟,只需要判断核酸开始营业时间,停业时间和来排队时间的先后顺序和计算题目中给出的公式即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct dot
{
int h1, m1, h2, m2, h3, m3;
}he[110];
int n;
int mi[110];
int arr[110][10];
ll ans;
void in()
{
for(int i = 1; i <= n; i++)
{
int h,m;
string s;
char a,b,c,d;
cin>>s;
a = s[0], b = s[1];
c = s[3], d = s[4];
h = (a - '0') * 10 + (b - '0');
m = (c - '0') * 10 + (d - '0');
he[i].h1 = h;
he[i].m1 = m;
cin>>s;
a = s[0], b = s[1];
c = s[3], d = s[4];
h = (a - '0') * 10 + (b - '0');
m = (c - '0') * 10 + (d - '0');
he[i].h2 = h;
he[i].m2 = m;
cin>>s;
a = s[0], b = s[1];
c = s[3], d = s[4];
h = (a - '0') * 10 + (b - '0');
m = (c - '0') * 10 + (d - '0');
he[i].h3 = h;
he[i].m3 = m;
if(he[i].h1 * 60 + he[i].m1 > he[i].h3 * 60 + he[i].m3)
{
he[i].h3 = he[i].h1;
he[i].m3 = he[i].m1;
}
cin>>mi[i];
for(int j = 1; j <= mi[i]; j++)
cin>>arr[i][j];
}
}
// 1440
void calc(int i)
{
int base = he[i].h1 * 60 + he[i].m1;
int y = (he[i].h2 - he[i].h1) * 60 + (he[i].m2 - he[i].m1);
int st = he[i].h1 * 60 + he[i].m1;
int pai = he[i].h3 * 60 + he[i].m3;
if(pai < st)
he[i].h3 = he[i].h1, he[i].m3 = he[i].m1;
for(int x = 0; x <= y; x++)
{
if(x + st < pai) continue;
ll xx = 1;
ll cnt = 0;
for(int j = 1; j <= mi[i]; j++)
{
cnt += (arr[i][j] * xx);
xx *= x;
}
cnt = fabs(sin(cnt) * y);
if(x + cnt <= y)
{
ans = min(ans, base + x + cnt);
}
}
}
void solve()
{
in();
ans = 1e8;
for(int i = 1; i <= n; i++)
{
calc(i);
}
if(ans == 1e8)
{
cout<<"Oh No!\n";
}
else
{
int h = ans / 60;
int m = ans % 60;
if(h < 10)
{
cout<<0;
cout<<h;
}
else
cout<<h;
cout<<":";
if(m < 10)
{
cout<<0;
cout<<m;
}
else
cout<<m;
cout<<endl;
}
}
int main()
{
//ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr);
int t = 1;
//cin>>t;
while(cin>>n)
{
solve();
}
return 0;
}
I
I比较玄学,队友搞了2小时+4发罚时还没出来
我的作法记录这一行中是否有元素\(a\)存在
如何处理询问
开一个10000大小的数组记录ans1, ans2元素是否各存在1次,ans1对应x,ans2对应y。
分别记录\(x\)和\(y\)存在的行,将这些行中不是\(x\)且不是\(y\)的元素出现次数 + 1;
最后答案就是满足:ans1[i] >= 1 && ans2[i] >= 1条件的元素个数
我这样写的询问运算次数\(10 \times 50 \times 500 \times 500 = 125,000,000\)。
询问时间复杂度\(\text{O(Tnqm)}\)
能过也是神奇
正解是用二进制存出现的行,我在线段树里见过这个,没想出来这个技巧
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
int m[51];
int a[51][510];
set<int> s[10010];
int ans[10010];
int ans2[10010];
bool st[10010];
int exist[51][10010];
void solve()
{
memset(exist, 0, sizeof exist);
for(int i = 1; i <= n; i++)
{
cin>>m[i];
for(int j = 1; j <= m[i]; j++)
{
cin>>a[i][j];
//s[a[i][j]].insert(i);
exist[i][a[i][j]] = 1;
}
}
int q; cin>>q;
while(q--)
{
int x, y; cin>>x>>y;
set<int> pos1, pos2;
memset(ans, 0, sizeof ans);
memset(ans2, 0, sizeof ans2);
for(int i = 1; i <= n; i++)
{
if(exist[i][x] == 1)
pos1.insert(i);
if(exist[i][y] == 1)
pos2.insert(i);
}
for(auto &it : pos1)
{
for(int i = 1; i <= m[it]; i++)
{
if(a[it][i] != x && a[it][i] != y)
{
//cout<<"X: "<<a[it][i]<<endl;
ans[a[it][i]]++;
}
}
}
for(auto &it : pos2)
{
for(int i = 1; i <= m[it]; i++)
{
if(a[it][i] != x && a[it][i] != y)
{
//cout<<"Y: "<<a[it][i]<<endl;
ans2[a[it][i]]++;
}
}
}
int res = 0;
for(int i = 1; i <= 10000; i++)
if(ans[i] >= 1 && ans2[i] >= 1)
res++;
cout<<res<<endl;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
int t = 1;
//cin>>t;
while(cin>>n)
{
solve();
}
return 0;
}
H
迪杰斯特拉算法 + 状压DP
起点\(s\)到甜品站\(x\),甜品站\(x\)出发到下一个甜品站,直到购买的甜品个数大于等于\(w\),再从甜品站\(y\)走到终点\(t\)的距离。观察甜品站的数量,可以很快的得知这里要用dijkstra对甜品站预处理,状压DP进行甜品站里之间的路径和处理
-
对每个甜品站进行dijkstra算法,赋\(f_{i,1 << i}\) 即为甜品站\(i\)到起点\(s\)的值
-
即可很快的写出转移方程\(f_{i,S}=\min f_{j,S-(1<<i)} + dist_{j,i}\),注意这里是0base,和代码不同,\(i\)代表已经访问了甜品站中,最后访问的甜品站,\(S\)代表访问了的甜品站的集合
-
对于所有\(S\)集合满足甜品站的甜品之和大于等于\(w\),答案为\(res = \min f_{i,S} + dist_{i,t}\)
更多细节由于语文水平,见代码
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
typedef pair<int, int> pii;
typedef long long ll;
const int N = 1e3 + 10;
vector<pii> e[N];
pii shop[20];
int n, m, k, s, t, w;
int dist[N][N];
bool vis[N][N];
int sum[1 << 17];
int f[20][1<<17];
void dijkstra(int st)
{
for(int i = 1; i <= n; i++) dist[st][i] = 1e9;
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({0, st});
dist[st][st] = 0;
while(q.size() >= 1)
{
auto t = q.top(); q.pop();
if(vis[st][t.se]) continue;
vis[st][t.se] = true;
for(auto &v : e[t.se])
{
if(dist[st][v.fi] > dist[st][t.se] + v.se)
{
dist[st][v.fi] = dist[st][t.se] + v.se;
q.push({dist[st][v.fi], v.fi});
}
}
}
}
/*
3 2 1 1 3 2
1 2 1
1 3 2
2 3
4 4 2 1 3 2
1 2 3
2 3 2
1 4 6
3 4 3
2 2
4 3
4 4 2 1 3 5
1 2 3
2 3 2
1 4 6
3 4 3
2 4
4 3
*/
void init()
{
for(int i = 1; i <= 1000; i++)
e[i].clear();
memset(f, 0x3f, sizeof f);
memset(sum, 0, sizeof sum);
memset(vis, false, sizeof vis);
memset(dist, 0x3f, sizeof dist);
}
void solve()
{
init();
cin>>m>>k>>s>>t>>w;
for(int i = 1; i <= m; i++)
{
int u, v, ww;
cin>>u>>v>>ww;
e[u].push_back({v, ww});
e[v].push_back({u, ww});
}
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= k; i++)
{
cin>>shop[i].fi>>shop[i].se;
}
//dijkstra(s);
//dijkstra(t);
for(int i = 1; i <= k; i++)
dijkstra(shop[i].fi);
for(int i = 1; i <= k; i++)
f[i][1 << (i - 1)] = dist[shop[i].fi][s];
for(int S = 0; S < (1 << k); S++)
for(int i = 1; i <= k; i++)
if(S & (1 << (i - 1)))
sum[S] += shop[i].se;
int res = 1e9;
for(int S = 0; S < (1 << k); S++)
{
for(int i = 1; i <= k; i++)
{
if(S & (1 << (i - 1)))
{
for(int j = 1; j <= k; j++)
{
if(i == j)
continue;
if(S & (1 << (j - 1)))
{
f[i][S] = min(f[j][S - (1 << (i - 1))] + dist[shop[j].fi][shop[i].fi], f[i][S]);
}
}
if(sum[S] >= w)
{
res = min(res, f[i][S] + dist[shop[i].fi][t]);
}
}
}
}
cout<<res<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
int t = 1;
//cin>>t;
while(cin>>n)
{
solve();
}
return 0;
}
本文来自博客园,作者:magicat,转载请注明原文链接:https://www.cnblogs.com/magicat/p/17325343.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号