SHOI2012信用卡凸包

信用卡是一个矩形，唯四个角作了圆滑处理，使它们都是与矩形的两边相切的 1/4 圆，如下图所示。

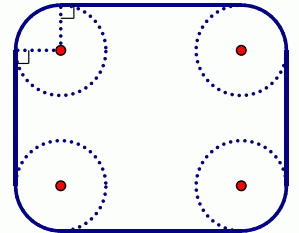
现在平面上有一些规格相同的信用卡，试求其凸包的周长。

注意凸包未必是多边形，因为它可能包含若干段圆弧。

输入格式

第一行是一个正整数 n，表示信用卡的张数。

第二行包含三个实数 a,b,r 分别表示信用卡（圆滑处理前）竖直方向的长度、水平方向的长度，以及 1/4 圆的半径。

之后 n 行，每行包含三个实数 x,y,θ，分别表示一张信用卡中心（即对角线交点）的横、纵坐标，以及绕中心逆时针旋转的弧度。

输出格式

输出只有一行，包含一个实数，表示凸包的周长，四舍五入精确到小数点后 2 位。

 

 

 

 

 

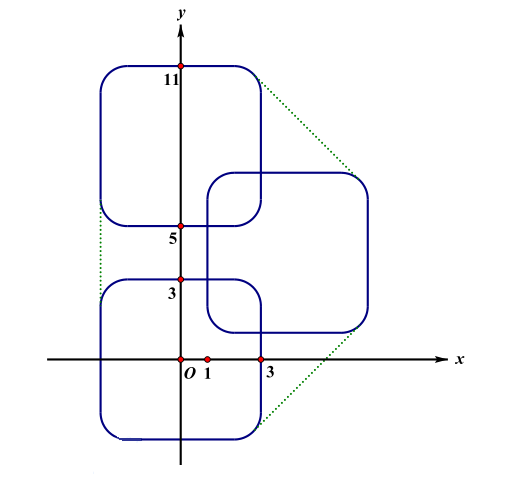
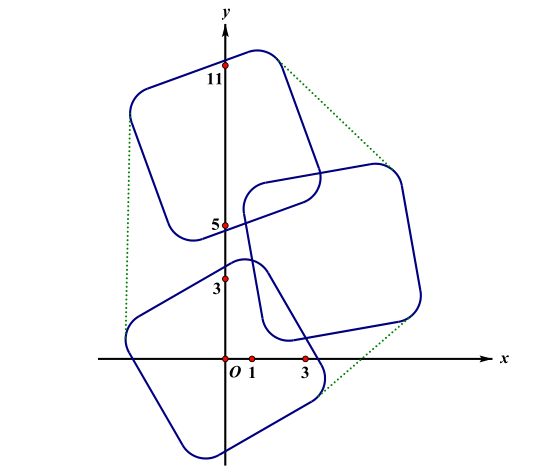
 这里需要对信用卡的长宽分别处理，原点加上边的一半减-r，即x=x+a/2-r,y=y+b/2-r，求出四个点，并旋转角度，求凸包

凸包各点距离加上圆的周长就是答案啦！

 

#include<iostream>
#include<algorithm>
#include<cmath>
#include<math.h>

using namespace std;
const double pi=acos(-1); 
struct Point
{
    double x,y;
    Point(double x=0,double y=0) :x(x),y(y) {} 
};
typedef Point Vector;

Vector operator + (Vector A,Vector B)
{
    return Vector(A.x+B.x,A.y+B.y);
}

Vector operator - (Vector A,Vector B)
{
    return Vector(A.x-B.x,A.y-B.y);
}
Vector operator * (Vector A,double p)
{
    return Vector(A.x*p,A.y*p);
}
Vector operator / (Vector A,double p)
{
    return Vector(A.x/p,A.y/p);
}

bool operator < (const Point& a,const Point& b)
{
    return a.x<b.x || (a.x==b.x&&a.y<b.y);
}

const double eps = 1e-10;

int dcmp(double x)
{
    if(fabs(x)<eps)         return 0;
    if(x<0)     return -1;
    return 1;
}

bool operator == (const Point& a,const Point& b)
{
    return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
}
double cross(Vector A,Vector B)
{
    return A.x*B.y-A.y*B.x;
}

double dot(Vector A,Vector B)
{
    return A.x*B.x+A.y*B.y;
}
double length(Vector A)
{
    return sqrt(dot(A,A));
}
Vector rotate(Vector A,double rad)
{
    return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
double convexhull(Point* p,int n,Point* ch)
{
    double res=0;
    sort(p,p+n);
    int m=0;
    for(int i=0;i<n;i++)
    {
        while(m>1 && cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)    m--;
        ch[m++]=p[i]; 
    }
    int k=m;
    for(int i=n-2;i>=0;i--)
    {
        while(m>k && cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)    m--;
        ch[m++]=p[i];
    }
    if(n>1) m--;

    for(int i=1;i<=m;i++)
    {
        res=res+length(ch[i]-ch[i-1]);
    }
    return res;
}

int main()
{
    int n,sum=0;
    double a,b,r;
    cin>>n>>a>>b>>r;
    a=a/2-r,b=b/2-r;
    int dx[]={1,1,-1,-1},dy[]={1,-1,-1,1};
    Point p[40010],ch[40010];
    for(int i=0;i<n;i++)
    {
        double x,y,ang;
        cin>>x>>y>>ang;
        for(int i=0;i<4;i++)
        {
            auto t=rotate({dx[i]*b,dy[i]*a},ang);
            p[sum++]=Vector{x+t.x,y+t.y};
        }
    }
    double res=convexhull(p,sum,ch);
    printf("%.2lf",res+pi*2*r);
    return 0;
}