第五章
本周学习了一下理论知识,然后这两天做一下实验,实现一下功能。
第五章 神经网络
5.1 神经元模型
神经元模型是一个包含输入,输出与计算功能的模型。输入可以类比为神经元的树突,而输出可以类比为神经元的轴突,计算则可以类比为细胞核。
下图是一个典型的神经元模型:包含有3个输入,1个输出,以及2个计算功能。
箭头称为“连接”。每个上有一个“权值”。
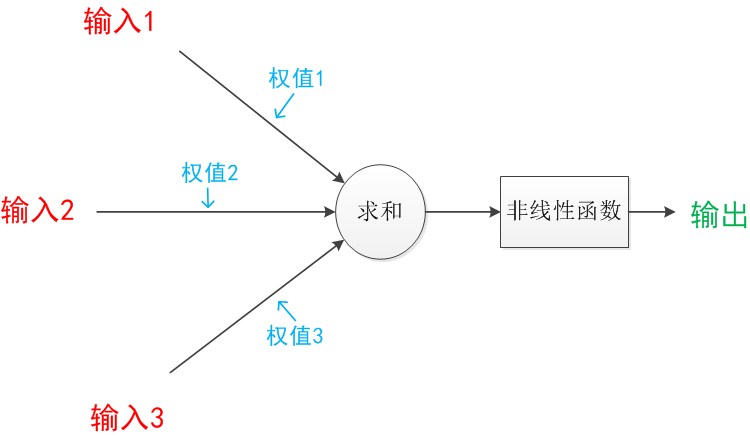
连接是神经元中最重要的东西。每一个连接上都有一个权重。一个神经网络的训练算法就是让权重的值调整到最佳,以使得整个网络的预测效果最好。这是M-P神经元模型。
其中的函数称为激活函数,最理想的是阶跃函数,但是因为不连续。所以用Sigmoid函数代替。
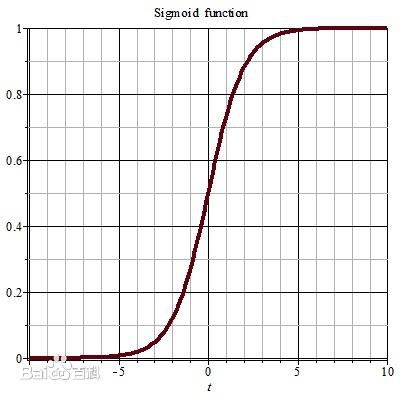
5.2 感知机与多层网络
感知机由两层神经元组成,输入层接受信号传给输出层,输出层是M-P神经元。
感知机可以实现与、或、非,但是因为层数过少,无法实现非线性可分的如异或等操作。
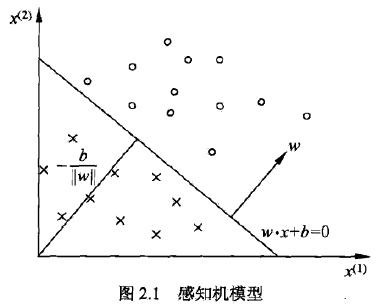
可以用一个超平面划分。
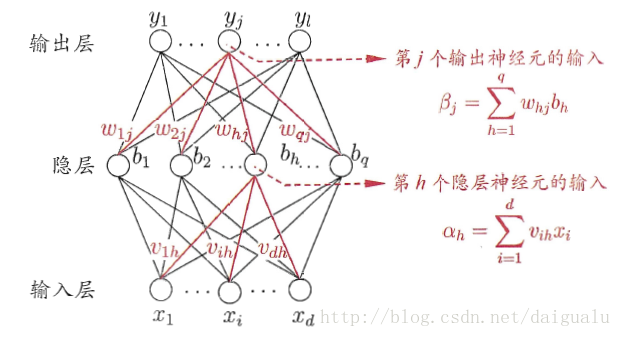
解决复杂问题,可以引入隐层,成为多层前馈神经网络。
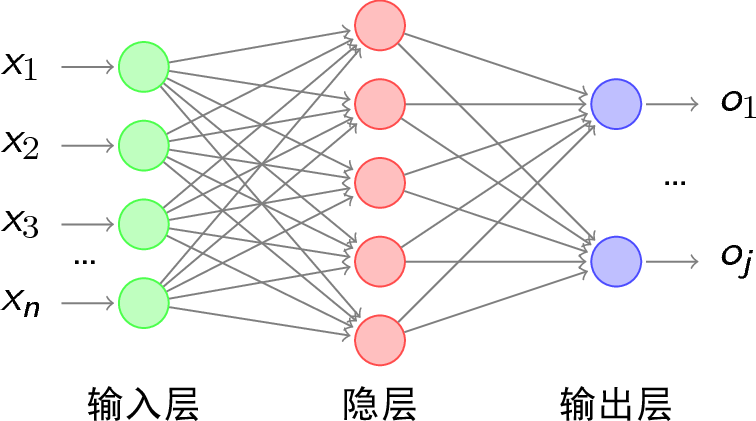
如图,含有一个隐层。
5.3 误差逆传播算法
简称BP算法。
误差反向传播法是Rumelhart等在1986年提出的,即BP(error BackPropagation)法影响最为广泛,也称BP算法。直到今天,BP算法仍然是自动控制上最重要、应用最多的有效算法。是用于多层神经网络训练的著名算法,有理论依据坚实、推导过程严谨、物理概念清楚、通用性强等优点。但是,人们在使用中发现BP算法存在收敛速度缓慢、易陷入局部极小等缺点。
BP算法大概是,将输入前传到输出,然后将输出回传到隐层神经元,然后,根据计算输出层的误差,调整连接权和阈值,不断重复,直到达到某些条件,结束算法,可以缩小误差。
5.4 全局最小与局部极小
和数学函数的最小值和极小值类似。
如图
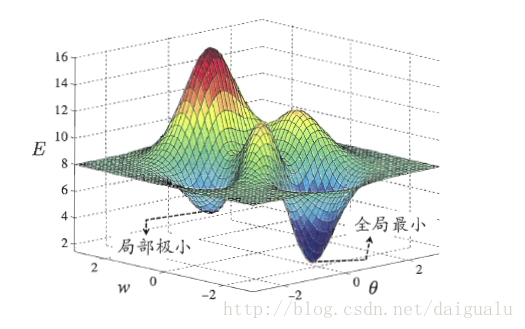
求局部极小可以用梯度下降算法,可以不断逼近极小值。
但是如果存在多个局部极小,那么就要跳出极小,进一步寻找全剧最小。
有一下三种策略:
1.用多种不同的参数值初始化神经网络,就像在山上从不同的点向下走,可以找到更多极小点。
2.模拟退火。模拟退火在每一步都接受比当前解更差的结果,从而有助于跳出局部极小,寻找次优解,随着迭代,尽量少的使用次优解,从而保证稳定。
3.使用随机梯度下降。
5.5 其他神经网络
- RBF网络
一种单隐层前馈网络 - ART网络
竞争型网络,每层只有一个神经元处于激活状态,其他均为抑制。 - SOM网络
将高维输入数据映射到低维空间。 - 级联相关网络
级联相关神经网络是从一个小网络开始,自动训练和添加隐含单元,最终形成一个多层的结构。级联相关神经网络具有以下优点:学习速度快;自己决定神经元个数和深度;训练集变化之后还能保持原有的结构;不需要后向传播错误信号。
- Elman网络
一种递归神经网络,可以出现环形结构,从而让一些神经元反馈回来作为输入信号。 - Boltzmann机
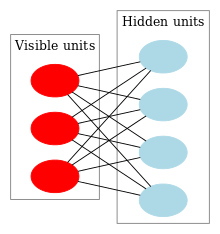
![image]()
如图所示为一个玻尔兹曼机,其蓝色节点为隐层,白色节点为输入层。
玻尔兹曼机和递归神经网络相比,区别体现在以下几点:
1、递归神经网络本质是学习一个函数,因此有输入和输出层的概念,而玻尔兹曼机的用处在于学习一组数据的“内在表示”,因此其没有输出层的概念。
2、递归神经网络各节点链接为有向环,而玻尔兹曼机各节点连接成无向完全图。
这里有个问题,就是在玻尔兹曼机里,各层连接均为回路,输出是如何产生的。
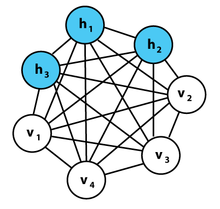
还有一种受限玻尔兹曼机
限制玻尔兹曼机和玻尔兹曼机相比,主要是加入了“限制”。所谓的限制就是,将完全图变成了二分图。如图所示,限制玻尔兹曼机由三个显层节点和四个隐层节点组成。限制玻尔兹曼机可以用于降维(隐层少一点),学习特征(隐层输出就是特征),深度信念网络(多个RBM堆叠而成)等。
5.6 深度学习
深度学习应用一些复杂的网络。表现就是,隐层很多,通常会有八九层。在计算力提升和大数据的时代得到了很好的应用。
可将深度学习理解为“特征学习”和“表示学习”。
常用的有CNN等。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号