深入理解计算机系统(第三版)作业题答案(第二章)
说明
我发现,当把这些题做完之后对本章知识的理解才算有点小进步。下边的答案主要参考了这两个网站:
- http://blog.csdn.net/zhanyu1990/article/details/24936663
- https://dreamanddead.gitbooks.io/csapp-3e-solutions/chapter2
2.58

原理是把指向一个int类型的指针强行改为指向char类型,一般来说一个char占8位,这就能判断出来取出的值是否大于1
int is_little_endian(){
int a = 1;
return *((char*)&a);
}
2.59

这个比较简单,主要考察如何获取某些位。
(x&0xFF) | (y&~0xFF)
2.60

i << 3表示i * 2^3, 其原理是找出需要替换的那些位,然后将其替换掉就行了。
unsigned replace_byte(unsigned x, unsigned char b, int i)
{
return (x & ~(0xFF<<(i<<3))) | (b << (i<<3));
}
位级整数编码规则


2.61

下边的内容跟书的题目有关系,需要根据实际情况。
A(!~x) // 比较简单,不解释
B(!x) // 同上
C(!~(x | (~0xFF))) // x的最低有效字节中的位都等于1
D(!(x >> ((sizeof(int) - 1) << 3))) // x的最高有效字节中的位都等于0
2.62
这个题我觉得在使用补码表示整数的机器上是没啥问题的
#include <stdio.h>
int int_shifts_are_arithmetic() {
int i = -1;
return (i >> 1) == -1;
}
int main(void) {
printf("%d", int_shifts_are_arithmetic());
}
2.63

#include <stdio.h>
unsigned srl(unsigned x, int k) {
int xsrl = (int)x >> k;
int w = 8 * sizeof(int);
unsigned z = 2 << (w - k -1);
return (z - 1) & xsrl;
}
int sra(int x, int k) {
int xsra = (unsigned)x >> k;
int w = sizeof(int) << 3;
unsigned z = 1 << (w - k - 1);
unsigned mask = z - 1;
unsigned right = xsra & mask;
unsigned left = ~mask & (~(z & xsra) + z);
return left | right;
}
int main(void) {
unsigned t1 = srl(100, 2);
unsigned t2 = (unsigned)100 >> 2;
printf("%d----%d \n", t1, t2);
int t3 = sra(100, 2);
int t4 = 100 >> 2;
printf("%d----%d \n", t3, t4);
int t5 = sra(-100, 2);
int t6 = -100 >> 2;
printf("%d----%d \n", t5, t6);
}
2.64

// 该题目要求,只要奇数位有1,就返回1,否则返回0
#include <stdio.h>
/* Return 1 when any odd bit of x equals 1, 0 otherwise.
Assume w = 32.
*/
int any_odd_one(unsigned x) {
return !!(x & 0x55555555);
}
int main(void) {
int result = any_odd_one((unsigned)5);
printf("The result of 5: %d \n", result);
int result1 = any_odd_one((unsigned)2);
printf("The result of 2: %d \n", result1);
}
2.65

// 该题目要求,只要二进制书中1的个数为奇数,就返回1,否则返回0
#include <stdio.h>
/* Return 1 when x contains an odd nuimber of 1s, 0 otherwise.
Assume w = 32.
*/
int odd_ones(unsigned x) {
// 这是第一层的处理,对某一位i而言,通过右移了一位,我们就获取到了i前边的那一位,把他们异或后,
// 得到的位的值为0或者1,1就表示和前边的一位中有奇数个1,0表示有偶数个1.
x ^= (x >> 1);
// 经过上边的处理后呢,x中每一位的值的意义就不同了,他表示该位和它前边的位1的个数是奇数还是偶数
// 此时我们再右移2位,就获得了i前边的前边的值j,这个值j表示j和前边一位1的个数是奇数还是偶数
// 异或后,的值就便是到j前边,一共四位1的个数是奇数还是偶数
x ^= (x >> 2);
// 后面的都是按照上边的原理依次类推的
x ^= (x >> 4);
x ^= (x >> 8);
x ^= (x >> 16);
return x & 1;
}
int main(void) {
int result = odd_ones((unsigned)5);
printf("The result of 5: %d \n", result);
int result1 = odd_ones((unsigned)7);
printf("The result of 3: %d \n", result1);
}
2.66

#include <stdio.h>
#include <assert.h>
// 1. 先使用或加位移让第一个1的后边都是1
// 2. 然后取非后右移一位后,最右边的1就是我们想要的掩码
// 3. 由于上边得到的那个1就是原值中的第一个1的位置,因此&上原值就清空了1前边的位
int leftmost_one(unsigned x) {
x |= x >> 1;
x |= x >> 2;
x |= x >> 4;
x |= x >> 8;
x |= x >> 16;
return x & (~x >> 1);
}
int main(void) {
assert(leftmost_one(0xff00) == 0x8000);
assert(leftmost_one(0x6600) == 0x4000);
return 0;
}
2.67

#include <stdio.h>
#include <assert.h>
int int_size_is_32() {
int set_msb = 1 << 31;
int beyond_msb = set_msb << 1;
return set_msb && !beyond_msb;
}
int int_size_is_32_for_16bit() {
int set_msb = 1 << 15 << 15 << 1;
int beyond_msb = set_msb << 1;
return set_msb && !beyond_msb;
}
int main(void) {
printf("1: %lu \n", sizeof(1));
printf("32: %d \n", int_size_is_32());
printf("16: %d \n", int_size_is_32_for_16bit());
}
2.68

#include <stdio.h>
#include <assert.h>
int lower_one_mask(int n) {
int w = sizeof(int) << 3;
return (unsigned)-1 >> (w - n);
}
int main(void) {
assert(lower_one_mask(6) == 0x3F);
assert(lower_one_mask(17) == 0x1FFFF);
assert(lower_one_mask(32) == 0xFFFFFFFF);
return 0;
}
2.69

#include <stdio.h>
#include <assert.h>
unsigned rotate_left(unsigned x, int n) {
int w = sizeof(int) << 3;
unsigned t = x << n;
unsigned t1 = x >> (w - n - 1) >> 1;
return t | t1;
}
int main(void) {
assert(rotate_left(0x12345678, 4) == 0x23456781);
assert(rotate_left(0x12345678, 20) == 0x67812345);
assert(rotate_left(0x12345678, 0) == 0x12345678);
return 0;
}
2.70

#include <stdio.h>
#include <assert.h>
// 如果x的二进制可以用n位表示就返回1,
/*
* Assume w = 8, n = 3
* if x > 0
* 0b00000110 is ok, 0b00001010 is not
* first w-n bits must be 0
* if x < 0
* 0b11111100 is ok, 0b10111100 is not, and 0b11111000 is not yet
* first w-n+1 bits must be 1
*/
int fits_bits(int x, int n) {
int w = sizeof(int) << 3;
x >>= n - 1;
/*
* !(x >> 1) 用于判断x大于0的情况
* !~x 用于判断x小于0的情况
*/
return !(x >> 1) || !~x;
}
int main(void) {
assert(fits_bits(0xFF, 8));
assert(!fits_bits(0xFFFFFF00, 8));
return 0;
}
2.71

#include <stdio.h>
#include <assert.h>
typedef unsigned packet_t;
// 该函数的作用是取出一个字中的某个字节,然后把该字节扩展为有符号整数
// 难点在于如何利用算数右移填充前边的位
// 核心思想就是先把目前字节左移到最高位,然后再利用算数右移
int xbyte(packet_t word, int bytenum) {
int size = sizeof(unsigned);
int shift_left_val = (size - 1 - bytenum) << 3;
int shift_right_val = (size - 1) << 3;
return (int)word << shift_left_val >> shift_right_val;
}
int main(void) {
assert(xbyte(0xAABBCCDD, 1) == 0xFFFFFFCC);
assert(xbyte(0x00112233, 2) == 0x11);
return 0;
}
2.72

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <string.h>
void copy_int(int val, void *buf, int maxbytes) {
if (maxbytes >= (int)sizeof(val)) {
memcpy(buf, (void *)&val, sizeof(val));
}
}
int main() {
int maxbytes = sizeof(int) * 10;
void *buf = malloc(maxbytes);
int val;
val = 0x12345678;
copy_int(val, buf, maxbytes);
assert(*(int *)buf == val);
val = 0x11111111;
val = 0xAABBCCDD;
copy_int(val, buf, 0);
assert(*(int *)buf != val);
return 0;
}
2.73

#include <stdio.h>
#include <assert.h>
#include <limits.h>
// 该函数是饱和加法,当正溢出,取最大整数,负溢出,取最小整数
int saturationg_add(int x, int y) {
int sum = x + y;
int sig_mask = INT_MIN;
// 如果x > 0 y > 0 sum < 0 正溢出
// 如果x < 0 y < 0 sum > 0 负溢出
int pos_over = !(x & sig_mask) && !(y & sig_mask) && (sum & sig_mask);
int neg_over = (x & sig_mask) && (y & sig_mask) && !(sum & sig_mask);
(pos_over && (sum = INT_MAX)) || (neg_over && (sum = INT_MIN));
return sum;
}
int main() {
assert(INT_MAX == saturationg_add(INT_MAX, 0x1234));
assert(INT_MIN == saturationg_add(INT_MIN, -0x1234));
assert(0x12 + 0x34 == saturationg_add(0x12, 0x34));
return 0;
}
2.74

#include <stdio.h>
#include <assert.h>
#include <limits.h>
// 该函数用于检查两个整数相减会不会产生溢出
// 这个和上边的题目很相似,可以把x-y看做x+(-y)
int tsub_ok(int x, int y) {
// 当y为最小整数的时候,就产生了溢出,因为任何数减最小数都会溢出
if (y == INT_MIN) {
return 0;
}
int neg_y = -y;
int sum = x + neg_y;
int pos_over = x > 0 && neg_y > 0 && sum < 0;
int neg_over = x < 0 && neg_y < 0 && sum >= 0;
return !(pos_over || neg_over);
}
int main(int argc, char* argv[]) {
assert(!tsub_ok(0x00, INT_MIN));
assert(tsub_ok(0x00, 0x00));
return 0;
}
2.75

/*
这个问题需要一步一步的进行推导
T2Uw(x)我们把这种写法称为补码转无符号数,那么很容易得出:
(2^w表示2的w次方,为什么当x<0时是这个结果呢,
其实,补码的负数就是把原来w-1之后的位的结果减去了最高一位的值,最高位的值就是2^w)
if x < 0 => x + 2^w
if x > 0 => x
上边的公式很简单,但在使用的时候还要做判断,显然很不科学,我们可以认为T2Uw(x)是一个函数
接下来就想办法推导出一个表达式来
这里省略了一系列的推导过程,得出了这样一个结果"
T2Uw(X)= X + X(w-1)2^w
大家看看这个式子跟上边的那个作用一样,x的w-1位就是他的最高位,如果该位的值是1,那么就相当于
x<0的情况,否则就是另一种情况
我们假设x`表示x的无符号值
X` = X + X(w-1)2^w
我们假设y`表示x的无符号值
Y` = Y + Y(w-1)2^w
那么X` * Y` = (X + X(w-1)2^w) * (Y + Y(w-1)2^w)
如果要把这个计算式展开会很麻烦,我们可以进一步抽象
设a = X(w-1)2^w, b= Y(w-1)2^w
则: X` * Y` = X*Y + X*b + Y*a + a*b
我们假定有这样一个函数,他的功能是取出无符号数的最高位uh(),因此上边的式子变形为:
uh(X` * Y`) = uh(X*Y + X*b + Y*a + a*b)
= uh(X*Y) + uh(X*b) + uh(Y*a) + uh(a*b)
那么X * b 也就是X*b= X*Y(w-1)2^w 他的最高位的值就是X*Y(w-1)2^w / 2^w => X*Y(w-1)
那么Y * a 也就是Y*a= Y*X(w-1)2^w 他的最高位的值就是Y*X(w-1)2^w / 2^w => Y*X(w-1)
那么a * b 也就是a*b= X(w-1)2^w * Y(w-1)2^w 他 / 2^w => 0
===> uh(X` * Y`) = uh(X*Y) + X*Y(w-1) + Y*X(w-1)
上边推理的核心思想就是 无符号X`的补码表示:X + X(w-1)2^w 求高位的/ 2^w 操作
*/
/*
* unsigned-high-prod.c
*/
#include <stdio.h>
#include <assert.h>
#include <inttypes.h>
int signed_high_prod(int x, int y) {
int64_t mul = (int64_t) x * y;
return mul >> 32;
}
unsigned unsigned_high_prod(unsigned x, unsigned y) {
/* TODO calculations */
int sig_x = x >> 31;
int sig_y = y >> 31;
int signed_prod = signed_high_prod(x, y);
return signed_prod + x * sig_y + y * sig_x;
}
/* a theorically correct version to test unsigned_high_prod func */
unsigned another_unsigned_high_prod(unsigned x, unsigned y) {
uint64_t mul = (uint64_t) x * y;
return mul >> 32;
}
int main(int argc, char* argv[]) {
unsigned x = 0x12345678;
unsigned y = 0xFFFFFFFF;
assert(another_unsigned_high_prod(x, y) == unsigned_high_prod(x, y));
return 0;
}
2.76

#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <assert.h>
#include <string.h>
void *another_calloc(size_t nmemb, size_t size) {
if (nmemb == 0 || size == 0) {
return NULL;
}
size_t buff_size = nmemb * size;
if (nmemb == buff_size / size) {
void *ptr = malloc(buff_size);
memset(ptr, 0, buff_size);
return ptr;
}
return NULL;
}
int main() {
void *p;
p = another_calloc(0x1234, 1);
assert(p != NULL);
free(p);
p = another_calloc(SIZE_MAX, 2);
assert(p == NULL);
free(p);
return 0;
}
2.77

#include <stdio.h>
#include <assert.h>
// K = 17
int A(int x) {
return (x << 4) + x;
}
// K = -7
int B(int x) {
return x - (x << 3);
}
// K = 60
int C(int x) {
return (x << 6) - (x << 2);
}
// K = -112
int D(int x) {
return (x << 4) - (x << 7);
}
int main() {
int x = 0x12345678;
assert(A(x) == x * 17);
assert(B(x) == x * -7);
assert(C(x) == x * 60);
assert(D(x) == x * -112);
printf("Passed.\n");
return 0;
}
2.78

#include <stdio.h>
#include <assert.h>
#include <limits.h>
// c语言的除法要求向0取整,除法本质上就是右移操作
int divide_power2(int x, int k) {
int is_neg = x & INT_MIN;
(is_neg && (x = x + (1 << k) - 1));
return x >> k;
}
int main(int argc, char* argv[]) {
int x = 0x80000007;
assert(divide_power2(x, 1) == x / 2);
assert(divide_power2(x, 2) == x / 4);
printf("%d", x);
return 0;
}
2.79
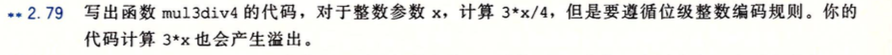
#include <stdio.h>
#include <limits.h>
#include <assert.h>
/*
* 在这个题目中的除以4中我们需要注意的是取整问题,因此需要用到题目2.78的函数
*/
int divide_power2(int x, int k) {
int is_neg = x & INT_MIN;
(is_neg && (x = x + (1 << k) -1));
return x >> k;
}
int mul3div4(int x) {
int mul3 = (x << 1) + x;
return divide_power2(mul3, 2);
}
int main() {
int t = 0x12345678;
assert(mul3div4(t) == (t * 3 / 4));
return 0;
}
2.80

#include <stdio.h>
#include <assert.h>
#include <limits.h>
/*
* 这个题目非常有意思,要保证不溢出,就要先做除法,也就是先除以4再乘以3
* 在下边中用到了一个非常巧妙的地方,把一个整数进行拆分
*/
/*
* calculate 3/4x, no overflow, round to zero
*
* no overflow means divide 4 first, then multiple 3, diffrent from 2.79 here
*
* rounding to zero is a little complicated.
* every int x, equals f(first 30 bit number) plus l(last 2 bit number)
*
* f = x & ~0x3
* l = x & 0x3
* x = f + l
* threeforths(x) = f/4*3 + l*3/4
*
* f doesn't care about round at all, we just care about rounding from l*3/4
*
* lm3 = (l << 1) + l
*
* when x > 0, rounding to zero is easy
*
* lm3d4 = lm3 >> 2
*
* when x < 0, rounding to zero acts like divide_power2 in 2.78
*
* bias = 0x3 // (1 << 2) - 1
* lm3d4 = (lm3 + bias) >> 2
*/
int threeforths(int x) {
int is_neg = x & INT_MIN;
int f = x & ~0x3;
int l = x & 0x3;
int fd4 = f >> 2;
int fd4m3 = (fd4 << 1) + fd4;
int lm3 = (l << 1) + l;
int bias = (1 << 1) + 1;
(is_neg && (lm3 += bias));
int lm3d4 = lm3 >> 2;
return fd4m3 + lm3d4;
}
int main(int argc, char* argv[]) {
assert(threeforths(8) == 6);
assert(threeforths(9) == 6);
assert(threeforths(10) == 7);
assert(threeforths(11) == 8);
assert(threeforths(12) == 9);
assert(threeforths(-8) == -6);
assert(threeforths(-9) == -6);
assert(threeforths(-10) == -7);
assert(threeforths(-11) == -8);
assert(threeforths(-12) == -9);
return 0;
}
2.81


#include <stdio.h>
#include <assert.h>
#include <limits.h>
int A(int k) {
return -1 << k;
}
int B(int k, int j) {
return ~A(k) << j;
}
int main(int argc, char* argv[]) {
assert(A(8) == 0xFFFFFF00);
assert(B(16, 8) == 0x00FFFF00);
printf("%d", -INT_MIN);
return 0;
}
2.82

/*
* 2.82.c
*/
#include <stdio.h>
#include <assert.h>
#include <limits.h>
#include "lib/random.h"
// 强调的是这个推导的过程
/* broken when x is INT_MIN */
int A(int x, int y) {
return (x < y) == (-x > -y);
}
/*
* right
*
* ((x + y) << 4) + y - x
* =>
* x << 4 - x + y << 4 + y
* =>
* x*16 - x + y*16 + y
* whether overflow or not, =>
* x*15 + y*17
*/
int B(int x, int y) {
return ((x + y) << 4) + y - x == 17 * y + 15 * x;
}
/*
* right
*
* ~x + ~y + 1
* =>
* ~x + 1 + ~y + 1 - 1
* =>
* -x + -y - 1
* =>
* -(x + y) - 1
* =>
* ~(x + y) + 1 - 1
* =>
* ~(x + y)
*/
int C(int x, int y) {
return ~x + ~y + 1 == ~(x + y);
}
/*
* right
*
* (ux - uy) == -(unsigned) (y - x)
* =>
* -(ux - uy) == (unsigned) (y - x)
* =>
* (ux - uy) == (unsigned) (x - y)
*/
int D(int x, int y) {
unsigned ux = (unsigned) x;
unsigned uy = (unsigned) y;
return (ux - uy) == -(unsigned) (y - x);
}
/*
* right
*
* x >> 2 << 2
* =>
* x & ~0x3
* =>
* x - num(00/01/10/11)
* =>
* ((x >> 2) << 2) <= x
*/
int E(int x, int y) {
return ((x >> 2) << 2) <= x;
}
int main(int argc, char* argv[]) {
init_seed();
int x = random_int();
int y = random_int();
assert(!A(INT_MIN, 0));
assert(B(x, y));
assert(C(x, y));
assert(D(x, y));
assert(E(x, y));
return 0;
}
2.83

/*
* A:
* 这个问题的关键是找到y,k 和整数x的关系
* 我们假设这个整数是x
* 那么x = 0.yyyyyyyy... 这个时候是无法得出结果的,并没有用到k
* 那么要想用到k,我们把x左移k为 x << k = y.yyyyyyyy...
* 上边的那个表达式中y.yyyyyyyyy... = Y + x
* 因此得出 x << k = Y + x === > x << k - x = Y == > x = Y/(2^k - 1)
* B:
* y = 101 == > k=3 Y=5 x=5/7
* y = 0110 == > k=4 Y=6 x=6/15
* y = 010011 == > k=6 Y=19 x=19/63
*/
2.84

#include <stdio.h>
#include <assert.h>
unsigned f2u(float x) {
return *(unsigned *)&x;
}
int float_le(float x, float y) {
unsigned ux = f2u(x);
unsigned uy = f2u(y);
unsigned sx = ux >> 31;
unsigned sy = uy >> 31;
return sx == sy ? (sx == 0 ? ux <= uy : ux >= uy) : sx > sy;
}
int main() {
assert(float_le(+0, -0));
assert(float_le(0, 3));
assert(float_le(-4.12, -0));
assert(float_le(-4, 4));
return 0;
}
2.85

A:
bias = 2^(k-1) - 1 =
v = 2^E + M
7.0 = 111.000 = 1.11000x2^2
E = 2 = e - bias ==> e = E + bias = 2 + bias = 1 + 2^(k-1) ==> 0 1000...001 1100...
B:
能够描述的最大的奇整数的位应该是111111......
而浮点数表示为1.111111...*2^n的样式,小数点后边应该有n个1 得到这些,我们就能计算出该浮点数的二进制表示
因此最大的奇整数位11111... 有n+1个1 也就是2^(n+1) - 1
E = n ==> e = E + bias = n + bias
==> 0 n + bias 11111...
C:
要想得到最小的规格数,M必须是1.00...的样式 E = 1 - bias
V = 2^(1-bias) 取倒数 ==> V = 2^(bias-1) ==> E = bias - 1
e = bias + E ==> e = 2bias -1 = 2(2^(k-1) - 1) - 1 = 2^k -3
==> 0 1111...101 000000
2.86
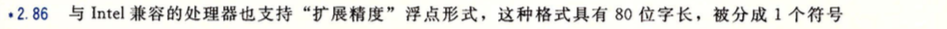

第一行答案:
最小的正非规格化数,要满足一下几个条件
1. 符号位为1
2. 阶码位全部为0
3. 单独的整数位为0
4. 小数位最后一位为1,其他都为0
得出的结论是: 0 000..00(15位) 0 000..01(63位)
偏量bias = 2^(k-1) - 1 = 2^(15-1) - 1 = 2^14 - 1
E = 1 - bias = 1 - 2^14 + 1 = 2 - 2^14
V = M * 2^E = 2^(-63) * 2^(2 - 2^14) = 2^(-63 + 2 - 2^14) = 2^(-61-2^14)
第二行答案:
最小的正规格数,满足下边几个条件
1. 符号位为0
2. 阶码位为1
3. 按照该题目要求,单独的整数位为1
4. 小数位全是0
得出的结论是: 0 000..01(15位) 1 000..00(63位)
偏量bias = 2^(k-1) - 1 = 2^(15-1) - 1 = 2^14 - 1
E = e - bias = 1 - 2^14 + 1 = 2 - 2^14
V = M * 2^E = 1 * 2^(2 - 2^14)
第三行答案:
最大的规格数,满足下边几个条件
1. 符号位为0
2. 阶码位全为1
3. 按照该题目要求,单独的整数位为1
4. 小数位全是1
得出的结论是: 0 111..10(15位) 1 111..11(63位)
偏量bias = 2^(k-1) - 1
E = e - bias = 2^15 - 2 - bias
V = M * 2^E = M * 2^(2^15 - 2 - bias) = M * 2^(2^14 * 2 - 2 - bias)
= M * 2^(2bias - bias) = M * 2^bias
此时M = 1 + (1 - 2^-63) = 2 - 2^-63
得出最终的结果是:2^bias * (2 - 2^-63)
2.87
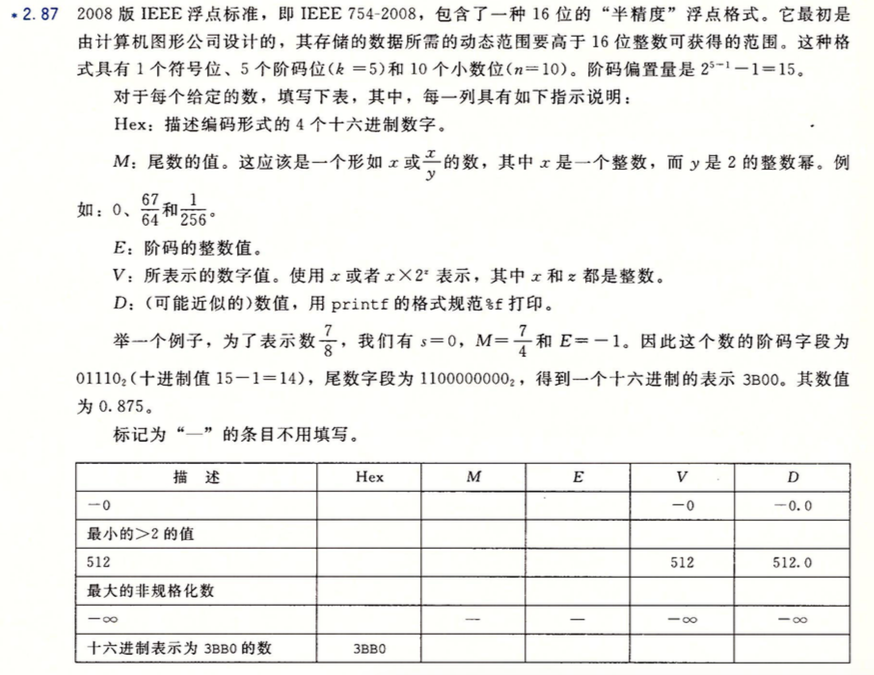
-0:
首先尾数M必须为0
阶码可以设置成00000 因此E = 1 - bias = 1 - 15 = -14
得到的位模式为:1 00000 0000000000 ==> 0x8000
最小的>2的值:
由M * 2^E ==> E = 1 M = 1.0000000001
E = e - bias ==> e = E + bias = 16 ==> e = 100000
M的值为2^-10 + 1 = 1025/1024
得到的位模式为:0 10000 0000000001 ==> 0x4001
V = 1025/1024 * 2 = 1025/512
512:
M = 1 E = 9 = e - bias ==> e = 9 + 15 = 24 ==> 11000
得到的位模式为:0 11000 0000000000 ==> 0x6000
最大的非规格化数:
非规格化数表示阶码位都是0 E= 1 - bias = -14
M 1023/1024
得到的位模式为:0 00000 1111111111 ==> 0x03FF
-oo:
1 11111 0000000000 ==> 0xFC00
十六进制表示为3BB0:
先把这个数展开:0011 1011 1011 0000 ==> 0 01110 1110110000
e = 14 E = e - bias = 14 - 15 = -1
M = 2^-1 + 2^-2 + 2^-3 + 2^-5 + 2^-6 = 59/64
V = M * 2^E = 59/64 * 2^-1 = 59/128
2.88

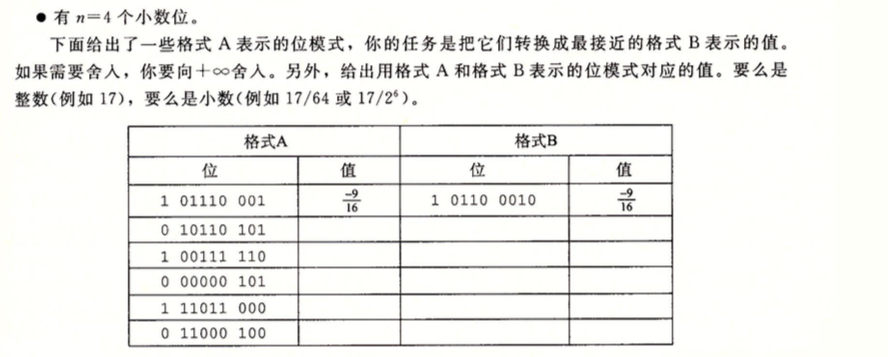
注意:如果是规格化的M = 1 + f 非规格化M = f
0 10110 101 :
A:
E = 22 - 15 = 7 V = (2^-1 + 2^-3 + 1) * 2^7 = 13 * 2^4
B:
通过观察,我们发现,先保持小数位不变,求阶码,如果不行,在改变小数位
因此B的 0 1110 1010 V = 13 * 2^4
1 00111 110:
A:
E = 7 - 15 = -8 (2^-1 + 2^-2 + 1) * 2^-8 = 7/4 * 2^-8 = -7/2^10
B:
1 0011 1110 ==> M = 1 + 2^-1 + 2^-2 + 2^-3 = 15/8
==> 2^E = (7/2^10) / (15/8) = 7/15 / 2^7 约等于2^-1*2^-7 = 2^-8
我们看看2^E的范围 2^-6 ~ 2^14
由于上边计算的2^-8不在这个范围中,因此需要调整阶码的值
先从最小的开始,设阶码为2^-6 那么 7/2^10 / 2^-6 = 7 / 16
==> (1/16 + 2/16 + 4/16) ==> (1/16 + 1/8 + 1/4) ==> (2^-4 + 2^-3 + 2^-2)
因此B的 0 0000 0111
0 00000 101:
A:
E = 1 - 15 = -14 V = (2^-1 + 2^-3) * 2^-14 = 5 * 2^-3 * 2^-14 = 5 * 2^-17 = 5/2^17
假设使用101作为尾数,那么M = (2^-1 + 2^-3 + 1) = 13 * 2^-3
2^E = V/M = 5/2^17 / (13 * 2^-3) = 5/17 * 2^-17 * 2^3 = 5/17 * 2^-14 显然你在范围之内
先从最小的开始,设阶码为2^-6 那么 5/2^17 / 2^-6 = 5 * 2^-11 显然B无法表示这个小数值
取一个最近似的 0 0000 0000
1 11011 000:
A:
E = 27 - 15 = 12 V = 2^12 取- 得-2^12
B:
由于这个值比较大,因此阶码取最大值1110 e = 14 E = e - 7 = 14 - 7 = 7 这样才能计算M的最小值
M = 2^12 / 2^7 = 2^5
显然M的值无法表示,因此阶码我们这次使用 1111 -oo
1 1111 0000
2.89

/*
* 2.89.c
*/
#include <stdio.h>
#include <assert.h>
#include <limits.h>
#include "lib/random.h"
/*
* most important thing is that all double number come from ints
*/
/* right */
int A(int x, double dx) {
return (float)x == (float)dx;
}
/* wrong when y is INT_MIN */
int B(int x, double dx, int y, double dy) {
return dx-dy == (double)(x-y);
}
/* right */
int C(double dx, double dy, double dz) {
return (dx+dy)+dz == dx+(dy+dz);
}
/*
* wrong
*
* FIXME I don't know what conditions cause false
*/
int D(double dx, double dy, double dz) {
return (dx*dy)*dz == dx*(dy*dz);
}
/* wrong when dx != 0 and dz == 0 */
int E(double dx, double dz) {
return dx/dx == dz/dz;
}
int main(int argc, char* argv[]) {
init_seed();
int x = random_int();
int y = random_int();
int z = random_int();
double dx = (double)x;
double dy = (double)y;
double dz = (double)z;
printf("%x %x %x\n", x, y, z);
assert(A(x, dx));
assert(!B(0, (double)(int)0, INT_MIN, (double)(int)INT_MIN));
assert(C(dx, dy, dz));
/* magic number, brute force attack */
assert(!D((double)(int)0x64e73387, (double)(int)0xd31cb264, (double)(int)0xd22f1fcd));
assert(!E(dx, (double)(int)0));
return 0;
}
2.90


/*
* fpwr2.c
*/
#include <stdio.h>
#include <assert.h>
#include <math.h>
float u2f(unsigned x) {
return *(float*) &x;
}
/* 2^x */
float fpwr2(int x) {
/* Result exponent and fraction */
unsigned exp, frac;
unsigned u;
/* 因为2^x 是大于0的,因此我们首先要确定浮点数能够表示的正非规格化数的最小值是
0 00000000 00000...001 ==> 2^-23 * 2^(1-bias) = 2^-23 * 2^(1-(2^7 - 1))
= 2^-23 * 2^(2-2^7)) = 2^(2 - 2^7 -23) = 2 - 128 - 23 = -149
*/
if (x < 2-pow(2,7)-23) {
/* too small. return 0.0 */
exp = 0;
frac = 0;
} else if (x < 2-pow(2,7)) {
/* Denormalized result */
/* 求出最小的规格化数
0 00000001 00000...000
E = 1 - 2^7 + 1 = 2 - 2^7 = -126 */
exp = 0;
/* 这段代码块求的值应该是非规格化数范围内的值
根据 V = M * 2^E V = 2^x ==> 2^x = M * 2^E
frac = M = 2^x / 2^E
E = 1 - bias = 2-2^7
frac = 2^(x - (2 - 2^7)) 这个是frac的值,但是我们如何获得它的位模式呢?
我们知道0 00000000 00000...001 最后边这个1对应的值是2^-23 也就是说
小数位的值和他的位模式有一个对应关系,我们只要求出frac是最后这个1(2^-23)的多少
倍,然后1 << 这个倍数就可以了,这样就得到了frac的位模式
*/
frac = 1 << (unsigned)(x - (2-pow(2,7)-23));
} else if (x < pow(2,7)-1+1) {
/* Normalized result */
/* 11111111 2^8 -1 - (2^7 - 1) ==> 2^8 - 2^7 -1 + 1 ==> 2^7
因此求exp 就等于求e e = E + bias = x + (2^7 - 1)
*/
exp = pow(2,7)-1+x;
frac = 0;
} else {
/* Too big, return +oo */
exp = 0xFF;
frac = 0;
}
/* pack exp and frac into 32 bits */
u = exp << 23 | frac;
/* Result as float */
return u2f(u);
}
int main(int argc, char* argv[]) {
assert(fpwr2(0) == powf(2,0));
assert(fpwr2(100) == powf(2,100));
assert(fpwr2(-100) == powf(2,-100));
assert(fpwr2(10000) == powf(2,10000));
assert(fpwr2(-10000) == powf(2,-10000));
return 0;
}
2.91

A:
0x40490FDB 展开后 0100 0000 0100 1001 0000 1111 1101 1011
换成小数的位模式: 0 10000000 10010010000111111011011
由于2^E = 2 V = 2M 我们知道M = 1.10010010000111111011011 那么2m
就相当于 << 1 得到:11.0010010000111111011011
B:
在问题2.83中我们得出这么一个公式:x = Y/(2^k - 1)
在本题中 x = 1/7 也就是说Y = 1 k = 3 说明Y是3位且值为1 因此就是001
所以最终的答案是11.001001001...(001)
C:
十进制小数转二进制数:“乘以2取整,顺序排列”(乘2取整法)
223/71 = 3.140845070422535 小数部分:0.140845070422535
0.140845070422535 * 2 = 0.28169014084507 ----- 取整 ----- 0
0.28169014084507 * 2 = 0.563380281690141 ----- 取整 ----- 0
0.563380281690141 * 2 = 1.126760563380282 ----- 取整 ----- 1
0.126760563380282 * 2 = 0.253521126760563 ----- 取整 ----- 0
0.253521 * 2 = 0.507042 ----- 取整 ----- 0
0.507042 * 2 = 1.014084 ----- 取整 ----- 1
0.014084 * 2 = 0.028168 ----- 取整 ----- 0
0.028168 * 2 = 0.056336 ----- 取整 ----- 0
0.056336 * 2 = 0.112672 ----- 取整 ----- 0
0.112672 * 2 = 0.225344 ----- 取整 ----- 0
因此在第9位就不同了
2.92

#include <stdio.h>
#include <assert.h>
typedef unsigned float_bits;
float_bits float_negate(float_bits f) {
unsigned sig = f >> 31;
unsigned exp = f >> 23 & 0xFF;
unsigned frac = f & 0x7FFFFF;
int is_nan = (exp == 0xFF && frac != 0);
if (is_nan) {
return f;
}
return ~sig << 31 | exp << 23 | frac;
}
int main() {
printf("%u", float_negate(32.0));
assert(float_negate(32.0) == -32.0);
return 0;
}
2.93

#include <stdio.h>
#include <assert.h>
typedef unsigned float_bits;
float_bits float_absval(float_bits f) {
unsigned exp = f >> 23 & 0xFF;
unsigned frac = f & 0x7FFFFF;
int is_nan = (exp == 0xFF && frac != 0);
if (is_nan) {
return f;
}
return 0 << 31 | exp << 23 | frac;
}
int main() {
printf("%u\n", float_absval(32.0));
return 0;
}
2.94

#include <stdio.h>
#include <assert.h>
typedef unsigned float_bits;
/*
* 要想实现浮点数*2,可以这么考虑 V = M * 2^E
* 当浮点数是规格数的时候,我们只需要改变E就行了,E = e - bias ==> 相当于给e的值+1
* 但是+1有个特殊情况,要是e的位模式为11111110 +1 就需要特殊处理
* 如果是非规格数, 那么 2^E就是固定的值,我们只能改变M的大小,*2就相当于把小数位左移一位
*/
float_bits float_twice(float_bits f) {
unsigned sig = f >> 31;
unsigned exp = f >> 23 & 0xFF;
unsigned frac = f & 0x7FFFFF;
int is_nan_or_oo = (exp == 0xFF);
if (is_nan_or_oo) {
return f;
}
if (exp == 0) {
frac <<= 1;
} else if (exp == 0xFE) {
exp = 0xFF;
frac = 0;
} else {
exp += 1;
}
return sig << 31 | exp << 23 | frac;
}
int main() {
printf("%u\n", float_twice(32.22));
return 0;
}
2.95

/*
* float-half.c
*/
#include <stdio.h>
#include <assert.h>
typedef unsigned float_bits;
float_bits float_half(float_bits f) {
unsigned sig = f >> 31;
unsigned rest = f & 0x7FFFFFFF;
unsigned exp = f >> 23 & 0xFF;
unsigned frac = f & 0x7FFFFF;
int is_NAN_or_oo = (exp == 0xFF);
if (is_NAN_or_oo) {
return f;
}
/*
* 这里就用到了向偶数取整的知识,在下边的注释中描述的很详细
* 那么如何理解取整呢,我们假设这个被右移出去的位为a,那么a就有可能是1或者0,如果是0,那么我们
就不需要取整,如果是1,我们可以这么想:1111.a 这个a如果是1,折算成小数就是0.5 因此是需要
取整的,它前边的那一位如果是0,表示已经是偶数了,就舍弃a 如果是1,要向上取整,在未右移之前+1就可以了
*/
/*
* round to even, we care about last 2 bits of frac
*
* 00 => 0 just >>1
* 01 => 0 (round to even) just >>1
* 10 => 1 just >>1
* 11 => 1 + 1 (round to even) just >>1 and plus 1
*/
int addition = (frac & 0x3) == 0x3;
if (exp == 0) {
/* Denormalized */
frac >>= 1;
frac += addition;
} else if (exp == 1) {
/* Normalized to denormalized */
rest >>= 1;
rest += addition;
exp = rest >> 23 & 0xFF;
frac = rest & 0x7FFFFF;
} else {
/* Normalized */
exp -= 1;
}
return sig << 31 | exp << 23 | frac;
}
2.96

#include <stdio.h>
#include <assert.h>
/*
我们首先考虑作为浮点数f能表示的最大的合法的整数是多少?
V = M * 2^E E = e - bias 由这两个公式可知E越大越好也就是e越大越好
e ==> 11111110 不能是11111111,
我们再考虑一个范围 0 <= f < 1 如果f在这个范围中,那么它的值就直接取0
我们要找出这个范围的浮点位模式,0:0 00000000 00000000000000000000000
1:0 01111111 00000000000000000000000
在上边的这个空间的值直接取0就行
那么f能表示的最大的合法的规格数是 0 11111110 111111111111111111111111
超过这个数的就成为越界了
如果在这个范围内:
E = exp - bias;
我们知道M的值的二进制小数是1.xxxxx... 但是下边M的值明显是做了<<23操作的,因此后边就要用E- 23
M = frac | 0x800000;
f = M * 2^E 根据这个公式,向0取整
if (E > 23) {
num = M << (E - 23);
} else {
num = M >> (23 - E);
}
*/
/*
* Compute (float) f
* If conversion cause overflow or f is NaN, return 0x80000000
*/
int float_f2i(float_bits f) {
unsigned sig = f >> 31;
unsigned exp = f >> 23 & 0xFF;
unsigned frac = f & 0x7FFFFF;
unsigned bias = 0x7F;
int num;
unsigned E;
unsigned M;
/*
* consider positive numbers
*
* 0 00000000 00000000000000000000000
* ===>
* 0 01111111 00000000000000000000000
* 0 <= f < 1
* get integer 0
*
* 0 01111111 00000000000000000000000
* ===>
* 0 (01111111+31) 00000000000000000000000
* 1 <= f < 2^31
* integer round to 0
*
* 0 (01111111+31) 00000000000000000000000
* ===>
* greater
* 2^31 <= f < oo
* return 0x80000000
*/
if (exp >= 0 && exp < 0 + bias) {
/* number less than 1 */
num = 0;
} else if (exp >= 31 + bias) {
/* number overflow */
/* or f < 0 and (int)f == INT_MIN */
num = 0x80000000;
} else {
E = exp - bias;
M = frac | 0x800000;
if (E > 23) {
num = M << (E - 23);
} else {
/* whether sig is 1 or 0, round to zero */
num = M >> (23 - E);
}
}
return sig ? -num : num;
}
2.97

/*
* float-i2f.c
*/
#include <stdio.h>
#include <assert.h>
#include <limits.h>
#include "float-i2f.h"
/*
* Assume i > 0
* calculate i's bit length
*
* e.g.
* 0x3 => 2
* 0xFF => 8
* 0x80 => 8
*/
int bits_length(int i) {
if ((i & INT_MIN) != 0) {
return 32;
}
unsigned u = (unsigned)i;
int length = 0;
while (u >= (1<<length)) {
length++;
}
return length;
}
/*
* generate mask
* 00000...(32-l) 11111....(l)
*
* e.g.
* 3 => 0x00000007
* 16 => 0x0000FFFF
*/
unsigned bits_mask(int l) {
return (unsigned) -1 >> (32-l);
}
/*
* Compute (float) i
*/
float_bits float_i2f(int i) {
unsigned sig, exp, frac, rest, exp_sig /* except sig */, round_part;
unsigned bits, fbits;
unsigned bias = 0x7F;
if (i == 0) {
sig = 0;
exp = 0;
frac = 0;
return sig << 31 | exp << 23 | frac;
}
if (i == INT_MIN) {
sig = 1;
exp = bias + 31;
frac = 0;
return sig << 31 | exp << 23 | frac;
}
sig = 0;
/* 2's complatation */
if (i < 0) {
sig = 1;
i = -i;
}
bits = bits_length(i);
fbits = bits - 1;
exp = bias + fbits;
rest = i & bits_mask(fbits);
if (fbits <= 23) {
frac = rest << (23 - fbits);
exp_sig = exp << 23 | frac;
} else {
int offset = fbits - 23;
int round_mid = 1 << (offset - 1);
round_part = rest & bits_mask(offset);
frac = rest >> offset;
exp_sig = exp << 23 | frac;
/* round to even */
if (round_part < round_mid) {
/* nothing */
} else if (round_part > round_mid) {
exp_sig += 1;
} else {
/* round_part == round_mid */
if ((frac & 0x1) == 1) {
/* round to even */
exp_sig += 1;
}
}
}
return sig << 31 | exp_sig;
}
总结
代码已上传github深入理解计算机系统第三版第二章作业题答案
如有错误之处,还请指正啊。。。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号