day 19 函数递归

1 二分法

算法：是高效解决问题的办法

算法之二分法

需求：有一个按照从小到大顺序排列的数字列表，需要从该数字列表中找到我们想要的那个一个数字，如何做更高效？？？

nums=[-3,4,7,10,13,21,43,77,89]
find_num=10
nums=[-3,4,13,10,-2,7,89]
nums.sort()
print(nums)

• 方案一：整体遍历效率太低

   for num in nums:
  	 if num == find_num:
  		 print('find it')
  		 break
  

• 方案二：二分法

   def binary_search(find_num,列表):
  	 mid_val=找列表中间的值
  	 
  	 if find_num > mid_val:
  		 binary_search(find_num,列表) #接下来的查找应该是在列表的右半部分, 列表=列表切片右半部分
  	 elif find_num < mid_val:
  		 binary_search(find_num,列表) #接下来的查找应该是在列表的左半部分,列表=列表切片左半部分
  	 else:
  		 print('find it')
  
   nums=[-3,4,7,10,13,21,43,77,89]
   find_num=8
  
   def binary_search(find_num,l):#
  	 if len(l) == 0:
  		 print('找的值不存在')
  		 return
  		 
  	 mid_index=len(l) // 2
  	 
  	 if find_num > l[mid_index]:  # 接下来的查找应该是在列表的右半部分
  		 l=l[mid_index+1:]
  		 binary_search(find_num,l)
  		 
  	 elif find_num < l[mid_index]:   # 接下来的查找应该是在列表的左半部分
  		 l=l[:mid_index]
  		 binary_search(find_num,l)
  		 
  	 else:
  		 print('find it')
  		 binary_search(find_num,nums)
  

2 函数递归

2.1 递归的定义

​ 函数不仅可以嵌套定义，还可以嵌套调用，即在调用一个函数的过程中，函数内部又调用另一个函数，而函数的递归调用指的是在调用一个函数的过程中又直接或间接地调用该函数本身

​ 函数的递归调用：是函数嵌套调用的一种特殊形式

​ 具体是指：在调用一个函数的过程中又直接或者间接地调用到本身

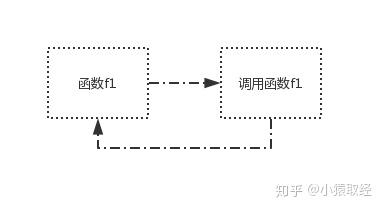
• 直接调用本身

   def f1():
  	 print('是我是我还是我')
  	 f1()
  	 
  f1()
  

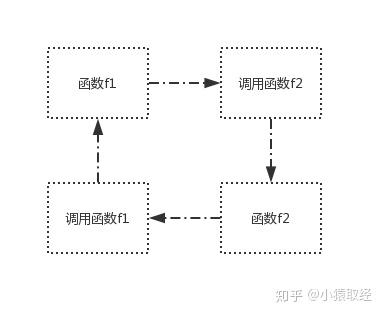
• 间接接调用本身，在调用f1的过程中，又调用f2，而在调用f2的过程中又调用f1，这就是间接调用函数f1本身

   def f1():
  	 print('===>f1')
  	 f2()
  
   def f2():
  	 print('===>f2')
  	 f1()
  
   f1()
  

一段代码的循环运行的方案有两种

• 方式一：while、for 循环

  while True:
  	 print(1111)
   	  print(2222)
  	 print(3333)
  

• 方式二：递归的本质就是循环：

  def f1():
  	 print(1111)
  	 print(2222)
  	 print(3333)
  	 f1()
  
   f1()
  

2.2 需要强调的的一点是：

递归调用不应该无限地调用下去，必须在满足某种条件下结束递归调用

 n=0
 while n < 10:# print(n)
	 n+=1

 def f1(n):
	 if n == 10:
		 return
	 print(n)
	 n+=1

 f1(0)

2.3 递归的两个阶段

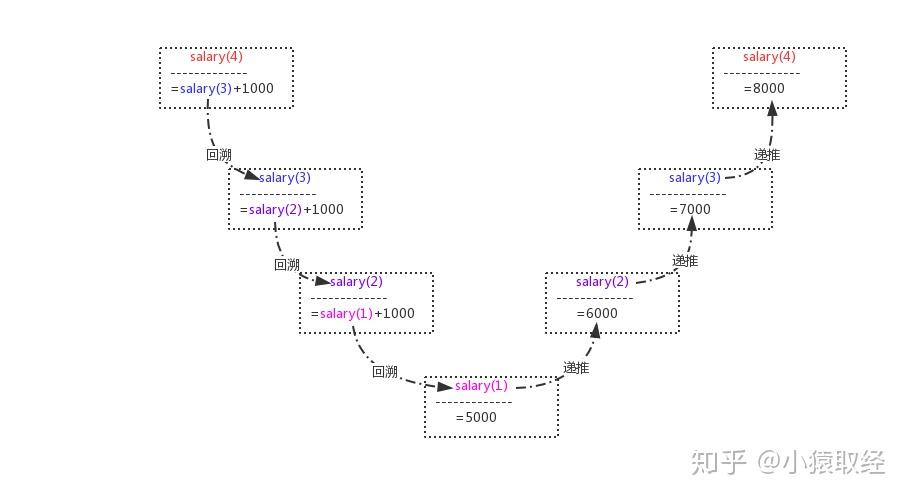
回溯：一层一层调用下去

递推：满足某种结束条件，结束递归调用，然后一层一层返回

 def age(n):
	 if n == 1:
		 return 18
	 return age(n-1) + 10

 res=age(5)
 age(5) = age(4) + 10
		  age(4) = age(3) + 10
 				   age(3) = age(2) + 10
							age(2) = age(1) + 10
 									 age(1) = 18
 									 
 print(res)

2.4 递归的应用

递归本质就是在做重复的事情，所以理论上递归可以解决的问题循环也都可以解决，只不过在某些情况下，使用递归会更容易实现，比如有一个嵌套多层的列表，要求打印出所有的元素，代码实现如下

 l=[1,2,[3,[4,[5,[6,[7,[8,[9,10,11,[12,[13,]]]]]]]]]]

 def f1(list1):
	 for x in list1:
		 if type(x) is list:       #如果是列表，应该再循环、再判断,即重新运行本身的代码
			 f1(x)
		 else:
			 print(x)

f1(l)

2.5 递归答疑

 nums=[-3,4,7,10,13,21,43,77,89]
 find_num=8
 
 def binary_search(find_num,l):
	 print(l)
	 if len(l) == 0:
		 print('找的值不存在')
		 return False
		 
	 mid_index=len(l) // 2
	 if find_num > l[mid_index]:
		 l=l[mid_index+1:] #接下来的查找应该是在列表的右半部分
		 return binary_search(find_num,l)

	 elif find_num < l[mid_index]:
		 l=l[:mid_index]  #接下来的查找应该是在列表的左半部分
		 return binary_search(find_num,l)

	 else:
		 print('find it')
		 return True

 res=binary_search(7,nums)
 print(res)

 def salary(n): # n = 3
	 if n==1:
		 return 5000

	 res=salary(n-1)+1000 # 6000 + 1000
	 return res

 res=salary(4) 
 	 salary(4)=salary(3)+1000
			   salary(3)=salary(2)+1000
						 salary(2)=salary(1) + 1000
								   salary(1)=5000