牛客小白月赛50解题报告

签到题，模拟即可，注意除法不是整除。

贪心

int res=0;
while(n>x){
    n/=2;
    res++;
}
while(n>0){
    n-=x;
    res++;
}

这题没看清楚，以为取余也要从数组中选择。实际上这是没必要的，只要在全体>1的自然数集合中取值即可。
这样的话问题就简单了，可以直接mod 2，但实际上这样还不对，比如5 10 15 20 0这样的数据就可以直接mod 5。

参考思路：
如果数组中所有数互质且至少存在一个>=2的数，则直接先mod 2再把所有还剩1的数都-1，共2次操作；
否则，可以mod 所有数的gcd，只需1次操作；
否则，若只存在0，则只需0次操作；
否则（即只存在0和1），只需1次操作。

	int a, n, gc = 0;
	bool f2 = 0, allZero = 1; //是否有>=2的
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d", &a);
		gc = gcd(gc, a);
		if (a > 0)	allZero = 0;
		if (a > 1)	f2 = 1;
	}
	//全为0
	if (allZero)
		putchar('0');
	//互质，则对2取余，那么剩下0和1。注意排除全<2的情况
	else if (gc == 1&&f2)
		putchar('2');
	//不互质
	else    putchar('1');

一开始看成两两异或再相加，后来发现不是这样。
不难发现最多不超过三人可能相同，因此只要罗列所有可能性并计算贡献即可。具体思路见代码，其中[i]=j表示第i天选择j作为“生日”。

if (n == 1)         res = 0;
else if (n == 2)    res = a[1] ^ a[2];
else {
    initPow(n);
    for (int i = 1; i <= n - 1; i++) {
	if (2 * i <= n) {
		int p = a[i] ^ a[i * 2];
		if (2 * i + 1 <= n) {
			//[i]=i,[i*2]=i,[i*2+1]=i+1
			p = (p * pow2[n - 3]) % MOD;
			res = (res + p) % MOD;
			// [i]=i,[i*2]=i,[i*2+1]=i
			p = ((a[i] ^ a[i * 2] ^ a[i * 2 + 1]) * pow2[n - 3]) % MOD;
			res = (res + p) % MOD;
			//[i]=i,[i*2]=i+1,[i*2+1]=i
			p = ((a[i] ^ a[2 * i + 1]) * pow2[n - 3]) % MOD;
			res = (res + p) % MOD;
		}
		//[i]=i,[i*2]=i
		else {
			p = (p * pow2[n - 2]) % MOD;
			res = (res + p) % MOD;
		}
	}
        //[i]=i/2,[i+1]=i/2
	if (i % 2 == 0) {
		int p = ((a[i] ^ a[i + 1]) * pow2[n - 3]) % MOD;
		res = ((res + p)) % MOD;
	}
    }
}

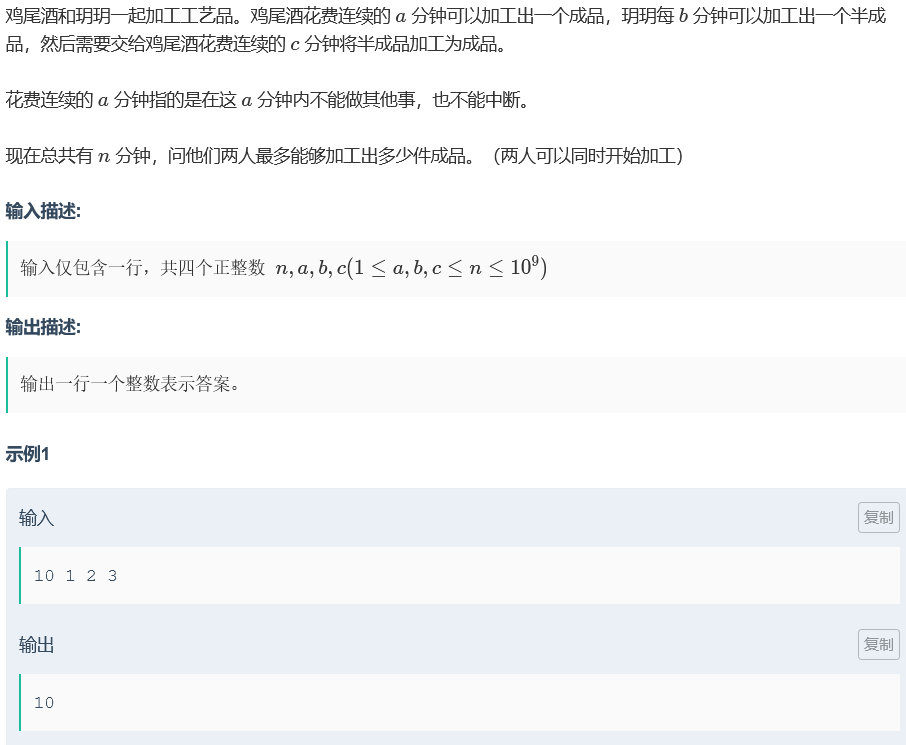
a < c:全部自己加工，否则：

1. b > c:可连续生产半成品，k件共需n=c+kb分钟,得k=(n-c)/b
2. b <= c:k件共需n=b+kc,得k=(n-b)/c

两种情况均可以对加工半成品(c)的时间进行“紧凑”。剩下的时间做成品

if(a<=c)    printf("%d",n/a);
else {
    int half=(b<=c)?(n-b)/c:(n-c)/b;
    //(n-c*half)/a:"紧凑"过后剩下的时间还能做多少成品
    printf("%d",half+(n-c*half)/a);
}