[机器学习笔记]奇异值分解SVD简介及其在推荐系统中的简单应用
本文先从几何意义上对奇异值分解SVD进行简单介绍,然后分析了特征值分解与奇异值分解的区别与联系,最后用python实现将SVD应用于推荐系统。
1.SVD详解
SVD(singular value decomposition),翻译成中文就是奇异值分解。SVD的用处有很多,比如:LSA(隐性语义分析)、推荐系统、特征压缩(或称数据降维)。SVD可以理解为:将一个比较复杂的矩阵用更小更简单的3个子矩阵的相乘来表示,这3个小矩阵描述了大矩阵重要的特性。
1.1奇异值分解的几何意义(因公式输入比较麻烦所以采取截图的方式)
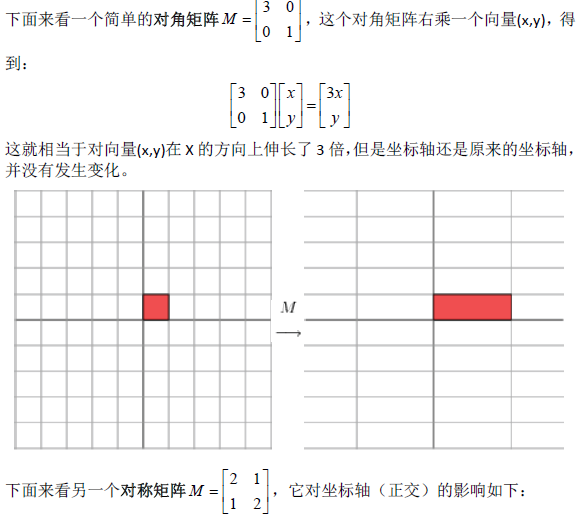
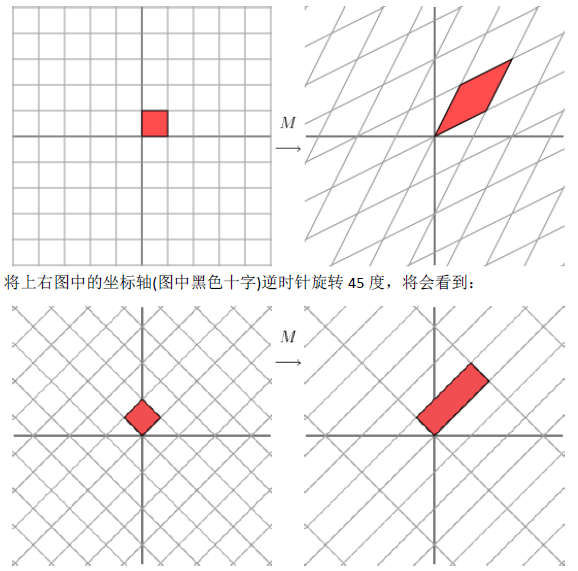

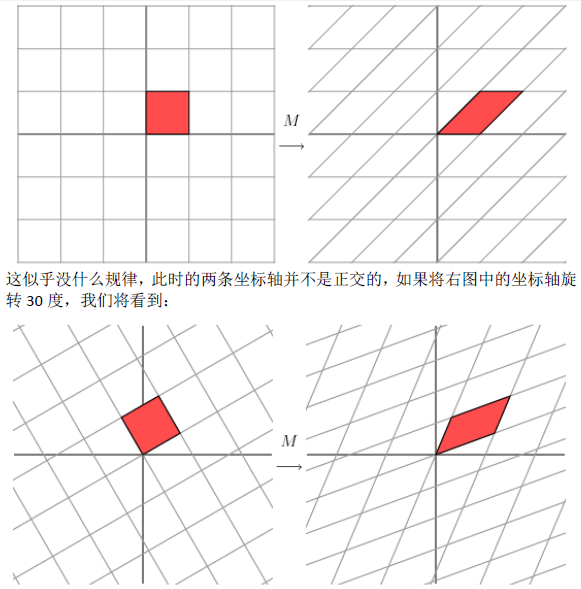
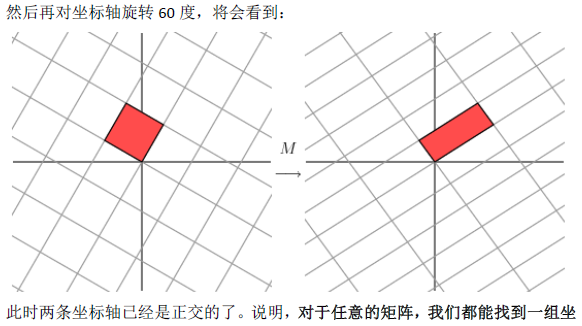
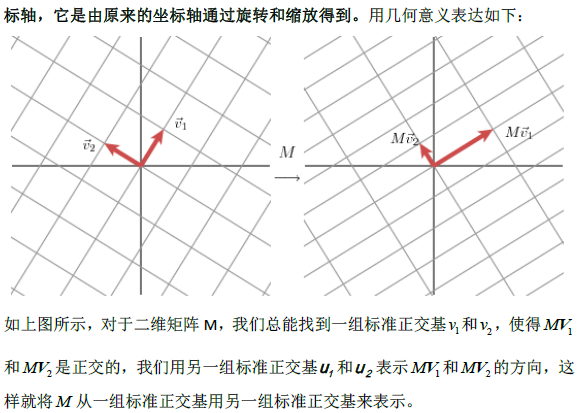








2.SVD应用于推荐系统
数据集中行代表用户user,列代表物品item,其中的值代表用户对物品的打分。基于SVD的优势在于:用户的评分数据是稀疏矩阵,可以用SVD将原始数据映射到低维空间中,然后计算物品item之间的相似度,可以节省计算资源。
整体思路:先找到用户没有评分的物品,然后再经过SVD“压缩”后的低维空间中,计算未评分物品与其他物品的相似性,得到一个预测打分,再对这些物品的评分从高到低进行排序,返回前N个物品推荐给用户。
具体代码如下,主要分为5部分:
第1部分:加载测试数据集;
第2部分:定义三种计算相似度的方法;
第3部分:通过计算奇异值平方和的百分比来确定将数据降到多少维才合适,返回需要降到的维度;
第4部分:在已经降维的数据中,基于SVD对用户未打分的物品进行评分预测,返回未打分物品的预测评分值;
第5部分:产生前N个评分值高的物品,返回物品编号以及预测评分值。
优势在于:用户的评分数据是稀疏矩阵,可以用SVD将数据映射到低维空间,然后计算低维空间中的item之间的相似度,对用户未评分的item进行评分预测,最后将预测评分高的item推荐给用户。
#coding=utf-8 from numpy import * from numpy import linalg as la '''加载测试数据集''' def loadExData(): return mat([[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5], [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3], [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0], [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0], [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0], [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0], [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1], [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4], [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2], [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0], [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]) '''以下是三种计算相似度的算法,分别是欧式距离、皮尔逊相关系数和余弦相似度, 注意三种计算方式的参数inA和inB都是列向量''' def ecludSim(inA,inB): return 1.0/(1.0+la.norm(inA-inB)) #范数的计算方法linalg.norm(),这里的1/(1+距离)表示将相似度的范围放在0与1之间 def pearsSim(inA,inB): if len(inA)<3: return 1.0 return 0.5+0.5*corrcoef(inA,inB,rowvar=0)[0][1] #皮尔逊相关系数的计算方法corrcoef(),参数rowvar=0表示对列求相似度,这里的0.5+0.5*corrcoef()是为了将范围归一化放到0和1之间 def cosSim(inA,inB): num=float(inA.T*inB) denom=la.norm(inA)*la.norm(inB) return 0.5+0.5*(num/denom) #将相似度归一到0与1之间 '''按照前k个奇异值的平方和占总奇异值的平方和的百分比percentage来确定k的值, 后续计算SVD时需要将原始矩阵转换到k维空间''' def sigmaPct(sigma,percentage): sigma2=sigma**2 #对sigma求平方 sumsgm2=sum(sigma2) #求所有奇异值sigma的平方和 sumsgm3=0 #sumsgm3是前k个奇异值的平方和 k=0 for i in sigma: sumsgm3+=i**2 k+=1 if sumsgm3>=sumsgm2*percentage: return k '''函数svdEst()的参数包含:数据矩阵、用户编号、物品编号和奇异值占比的阈值, 数据矩阵的行对应用户,列对应物品,函数的作用是基于item的相似性对用户未评过分的物品进行预测评分''' def svdEst(dataMat,user,simMeas,item,percentage): n=shape(dataMat)[1] simTotal=0.0;ratSimTotal=0.0 u,sigma,vt=la.svd(dataMat) k=sigmaPct(sigma,percentage) #确定了k的值 sigmaK=mat(eye(k)*sigma[:k]) #构建对角矩阵 xformedItems=dataMat.T*u[:,:k]*sigmaK.I #根据k的值将原始数据转换到k维空间(低维),xformedItems表示物品(item)在k维空间转换后的值 for j in range(n): userRating=dataMat[user,j] if userRating==0 or j==item:continue similarity=simMeas(xformedItems[item,:].T,xformedItems[j,:].T) #计算物品item与物品j之间的相似度 simTotal+=similarity #对所有相似度求和 ratSimTotal+=similarity*userRating #用"物品item和物品j的相似度"乘以"用户对物品j的评分",并求和 if simTotal==0:return 0 else:return ratSimTotal/simTotal #得到对物品item的预测评分 '''函数recommend()产生预测评分最高的N个推荐结果,默认返回5个; 参数包括:数据矩阵、用户编号、相似度衡量的方法、预测评分的方法、以及奇异值占比的阈值; 数据矩阵的行对应用户,列对应物品,函数的作用是基于item的相似性对用户未评过分的物品进行预测评分; 相似度衡量的方法默认用余弦相似度''' def recommend(dataMat,user,N=5,simMeas=cosSim,estMethod=svdEst,percentage=0.9): unratedItems=nonzero(dataMat[user,:].A==0)[1] #建立一个用户未评分item的列表 if len(unratedItems)==0:return 'you rated everything' #如果都已经评过分,则退出 itemScores=[] for item in unratedItems: #对于每个未评分的item,都计算其预测评分 estimatedScore=estMethod(dataMat,user,simMeas,item,percentage) itemScores.append((item,estimatedScore)) itemScores=sorted(itemScores,key=lambda x:x[1],reverse=True)#按照item的得分进行从大到小排序 return itemScores[:N] #返回前N大评分值的item名,及其预测评分值
将文件命名为svd2.py,在python提示符下输入:
>>>import svd2 >>>testdata=svd2.loadExData() >>>svd2.recommend(testdata,1,N=3,percentage=0.8)#对编号为1的用户推荐评分较高的3件商品
Reference:
1.Peter Harrington,《机器学习实战》,人民邮电出版社,2013
2.http://www.ams.org/samplings/feature-column/fcarc-svd (讲解SVD非常好的一篇文章,对于理解SVD非常有帮助,本文中SVD的几何意义就是参考这篇)
3. http://blog.csdn.net/xiahouzuoxin/article/details/41118351 (讲解SVD与特征值分解区别的一篇文章)



