LeetCode 07 - 二分查找

注意几个点：

• 区间的确定：一般写成闭区间 [left=0, right=n-1] 。
• 循环条件的确定：因为使用闭区间，所以 left==right 在区间中是有意义的，所以循环条件为 while(left <= right) 。
• 左右端点的更新：这在存在重复元素的情况下比较容易弄错，对于寻找指定数字左右边界的情况，在 nums[mid] == target 时，不像无重复情况那样直接返回，需要继续更新 left / right，进一步逼近边界。

33. 搜索旋转排序数组

所谓旋转排序，例如 [1,2,3,4,5] 在 3 处旋转变成 [3,4,5,1,2] 。

方法：二分

1. 首先按二分法对数组等分，此时 一定有一半是排好序的；
2. 检查目标值是否包含在排好序的那一半之内，如果是则用传统的二分法来搜索；
3. 否则对另一半继续二分，回到第 1 步，重复这个广义的二分过程。

那么 如何确定哪一半是有序的？很简单，如果开头的数小于结尾的数就是有序的。

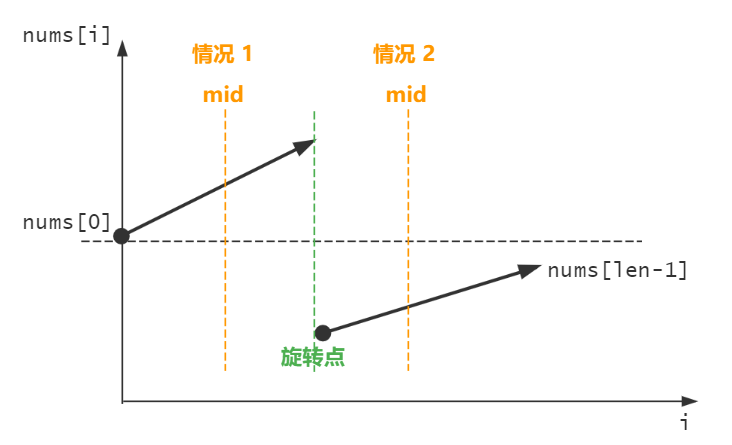
mid 的位置分成两种情况：

• mid 左边部分有序；
• mid 右边部分有序。

在每种情况中，如果目标值落在了这个有序部分中，则更新左指针或右指针的值：

• 如果落在了情况 1 的有序部分，则更新右指针为 mid-1 ；
• 如果落在了情况 2 的有序部分，则更新左指针为 mid+1 。

如果 没有落在有序部分中，则问题变成了 原问题的一个子问题：

• 如果落在情况 1 的无序部分，则更新左指针为 mid+1 ；
• 如果落在情况 2 的无序部分，则更新右指针为 mid-1 。

int search(int[] nums, int target) {
    int len = nums.length;
    if(len == 0) return -1;
    if(len == 1) return nums[0] == target ? 0 : -1;
    // 开始二分
    int left = 0, right = len-1;
    while(left <= right) {
        int mid = (right - left)/2 + left;
        int midValue = nums[mid];
        if(midValue == target) return mid;
        if(nums[0] <= midValue) { // 如果 mid 左边有序
            // 如果 target 在有序部分内
            if(nums[0] <= target && target < nums[mid])
                right = mid - 1;
            else // 如果 target 在无序部分内
                left = mid + 1;
        } else { // 如果mid 右边有序
            // 如果 target 在有序部分内
            if(nums[mid] < target && target <= nums[len-1])
                left = mid + 1;
            else // 如果 target 在无序部分
                right = mid - 1;
        }
    }
    return -1;
}

153. 寻找旋转排序数组中的最小值

方法：二分

注意一个现象：最小值到倒数第二个元素都小于最后一个元素 x，而在最小值左侧的所有元素都大于 x，所以可以用二分方法找到最小值。

两种情况：

• nums[mid] < x，说明可以忽略二分的后半部分数组；

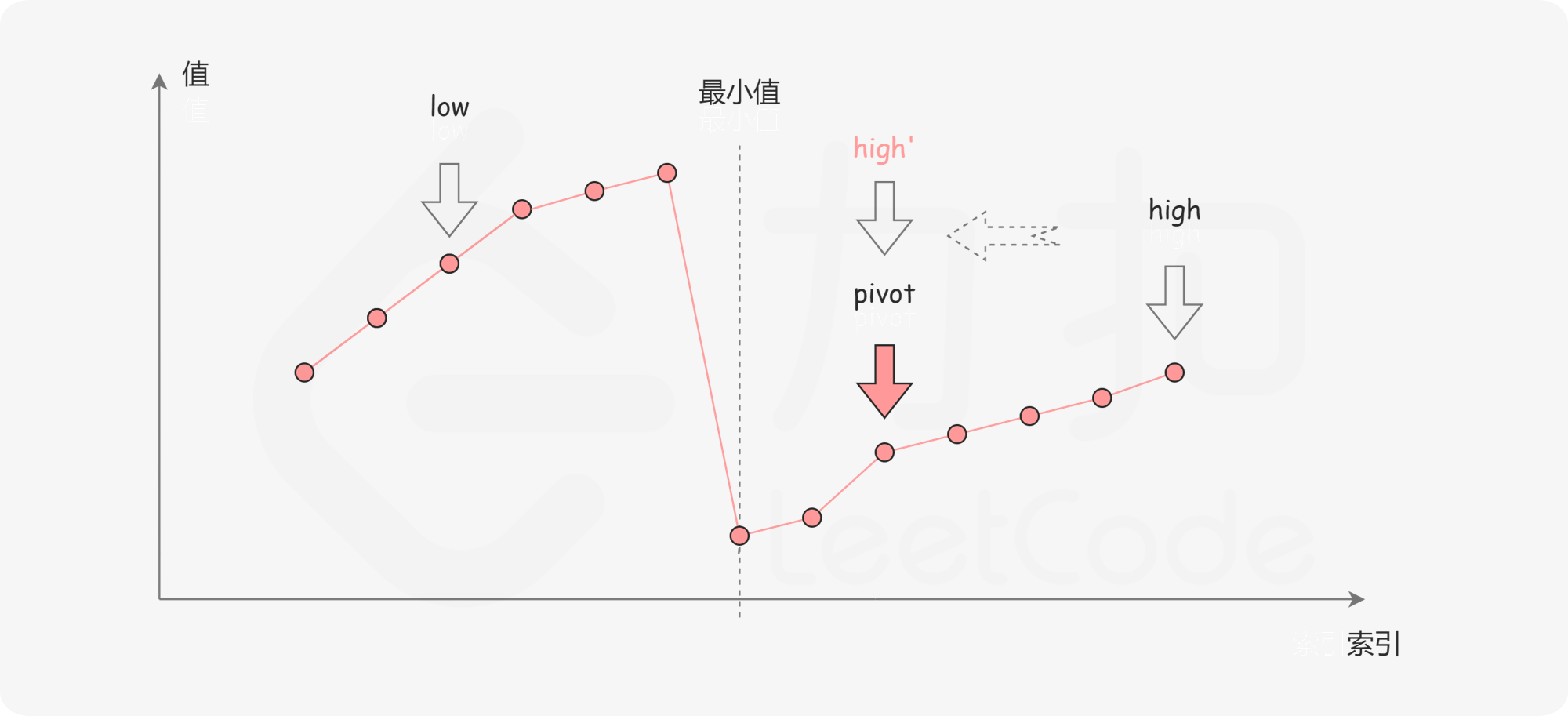
• nums[mid] > x，说明可以忽略二分的前半部分数组。

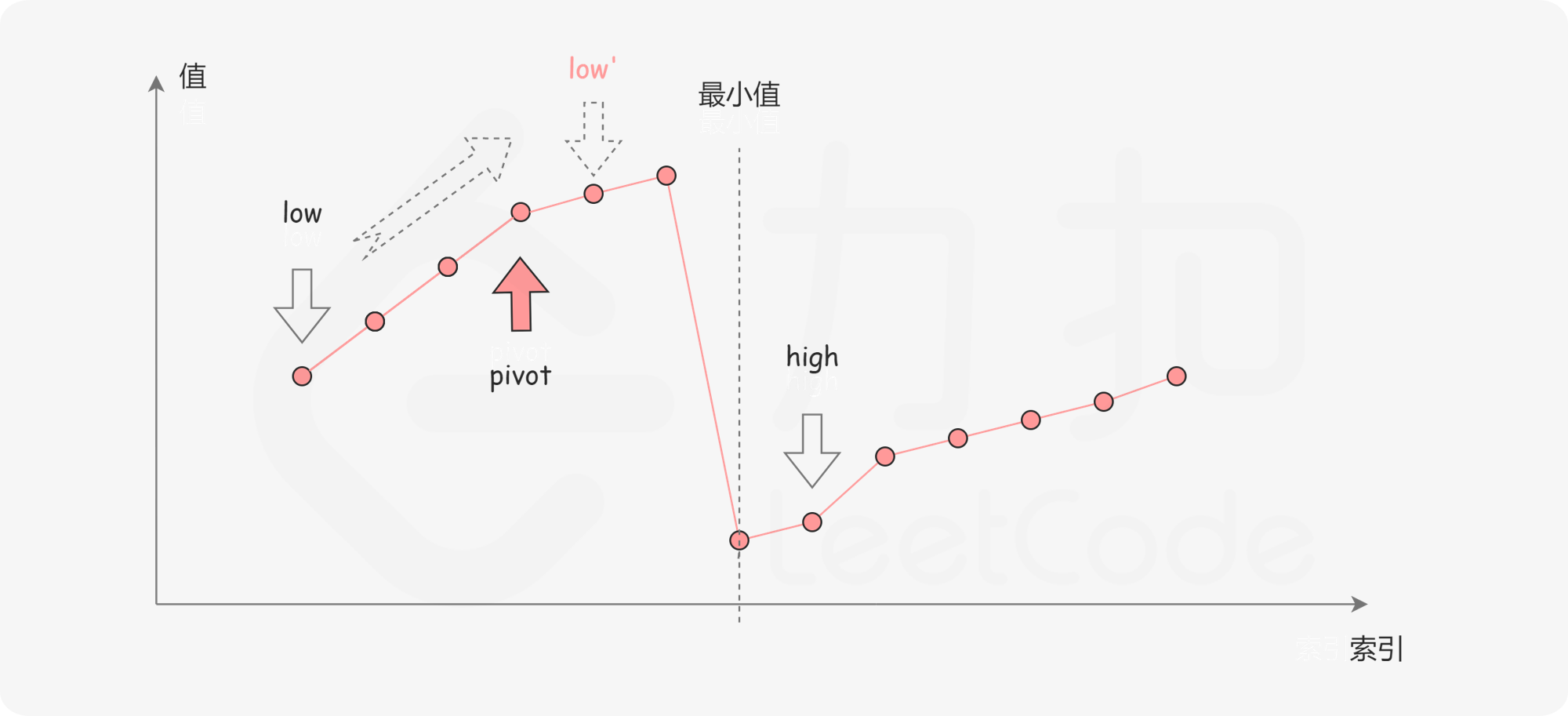
当区间为 1 时，就可以结束循环，此时 left 就是最小值的位置，所以循环条件是 left < right 。也正因为如此，mid 和 x 不会重合。

right = len - 1 ，left < right ，right = mid 。
区间 [left, right] 要保证始终包含结果。

int findMin(int[] nums) {
    int len = nums.length;
    int left = 0, right = len - 1; // 闭区间
    while(left < right) { // left == right 时结束
        int mid = left + (right - left) / 2; // 地板除，mid 可能等于 left
        if(nums[mid] < nums[len - 1])
            right = mid; // mid 可能是最小值
        else
            left = mid + 1; // mid 不可能是最小值（因为循环中数组长度至少为 2）
    }
    return nums[left];
}

34. 在排序数组中查找元素的第一个和最后一个位置

方法：二分

查找最左位置和最右位置的写法有些区别：

int findLeft(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while(left <= right) {
        int mid = left + (right - left) / 2;
        int midValue = nums[mid];
        if (midValue < target) 
            left = mid + 1;
        else if (midValue > target)
            right = mid - 1;
        else if (midValue == target) {
            // mid 已经是最左边了
            if (mid == 0 || nums[mid-1] != target)
                return mid;
            right = mid - 1; // mid 不是最左边，继续向左逼近
        }
    }
    return -1;
}

int findRight(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while(left <= right) {
        int mid = left + (right - left) / 2;
        int midValue = nums[mid];
        if (midValue < target)
            left = mid + 1;
        else if (midValue > target)
            right = mid - 1;
        else if (midValue == target){
            // mid 已经是最右边了
            if (mid == nums.length - 1 || nums[mid+1] != target)
                return mid;
            // 否则继续向右逼近
            left = mid + 1;
        }
    }
    return -1;
}

162. 寻找峰值

题目保证相邻的两个元素不相等，且 nums[-1] = nums[n] = -∞ .

方法一：寻找第一个满足 nums[i] > nums[i+1] 的元素。(\(O(n)\))

这样的元素同时也满足了 nums[i] > nums[i-1] ，因为是 「第一个」。

int findPeak(int[] nums) {
    int len = nums.length;
    for(int i = 0; i < len-1; i++)
        if(nums[i] > nums[i+1])
            return i;
    return len-1;
}

方法二：二分（\(O(logn)\)）

不断往高处走，一定可以到达一个峰值位置。

• 对于当前可行的下标范围 [l,r]，我们随机一个下标 i；
• 如果下标 i 是峰值，我们返回 i 作为答案；
• 如果 nums[i] < nums[i+1]，说明往右走一定能到达一个峰值，那么我们抛弃 [l,i] 的范围，在剩余 [i+1,r] 的范围内继续随机选取下标；
• 如果 nums[i] > nums[i+1]，说明往左走一定能到达一个峰值，那么我们抛弃 [i,r] 的范围，在剩余 [l,i−1] 的范围内继续随机选取下标。

所以，不一定在单调序列上才能用二分，只要满足“二段性”即可，所谓二段性，即：

• 一段满足某个条件，另一段不满足；
• 一段肯定满足某个条件，另一段不一定满足。

区间长度减小为 1 时，说明这就是个峰值，所以循环条件是 left < right 。

int findPeak(int[] nums) {
    int left = 0, right = nums.length - 1;
    while(left < right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] < nums[mid+1])
            left = mid + 1;
        else
            right = mid; // 不能是 mid - 1，因为 mid 可能就是峰值
    }
    return left;
}

240. 搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

方法一：二分搜索

boolean searchMatrix(int[][] matrix, int target) {
    for(int[] row : matrix) {
        int index = search(row, target);
        if(index >= 0) return true;
    }
    return false;
}

int search(int[] nums, int target) {
    int left = 0, right = nums.length-1;
    while(left <= right) {
        int mid = (right-left)/2 + left;
        int num = nums[mid];
        if(num == target) return mid;
        else if(num > target) right = mid-1;
        else left = mid+1;
    }
    return -1;
}

方法二：Z字形查找

从矩阵右上角开始搜索，在每一步搜索过程中，假设当前位置为 \((x,y)\)（x 表示行，y 表示列），那么搜索范围可以确定为：以矩阵左下角为左下角、以当前位置为右上角的子矩阵。

• 如果 matrix[x][y] = target 说明搜索完成。
• 如果 matrix[x][y] > target ，因为当前列 y 是递增的，所以当前列的所有元素一定都大于 target（在搜索范围内），所以可以直接将 y 减一。
• 同样地，如果 matrix[x][y] < target ，因为当前行 x 是递增的，所以当前行的其他元素一定都小于 target（在搜索范围内），所以可以直接将 x 加一。
• 如果超过矩阵边界，说明不存在 target。

boolean searchMatrix(int[][] matrix, int target) {
    int rows = matrix.length, cols = matrix[0].length;
    int x = 0, y = cols-1;
    while(x < rows && y >= 0) {
        if(matrix[x][y] == target) return true;
        if(matrix[x][y] > target) y--;
        else x++;
    }
    return false;
}