正则化

1、过拟合、欠拟合

　　过拟合是指模型在训练集上表现很好，在测试集上表现很差。欠拟合是指在训练集测试集上表现都很差。

 

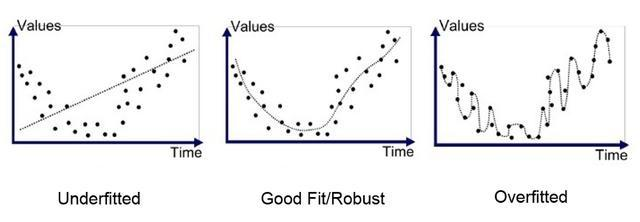
 上图左图是欠拟合，右图是过拟合的表现。

欠拟合的解决方法

解决方法：

1）添加其他特征项，有时候我们模型出现欠拟合的时候是因为特征项不够导致的，可以添加其他特征项来很好地解决。

2）添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。

3）减少正则化参数，正则化的目的是用来防止过拟合的，但是现在模型出现了欠拟合，则需要减少正则化参数。

4）可以增加迭代次数继续训练

5）尝试换用其他算法

6）增加模型的参数数量和复杂程度

过拟合的解决方法：

1）重新清洗数据，导致过拟合的一个原因也有可能是数据不纯导致的，如果出现了过拟合就需要我们重新清洗数据。

2）增大数据的训练量，还有一个原因就是我们用于训练的数据量太小导致的，训练数据占总数据的比例过小。

3）采用正则化方法。正则化方法包括L0正则、L1正则和L2正则，而正则一般是在目标函数之后加上对于的范数。

4）针对神经网络，可以采用dropout方法，间接减少参数数量，也相当于进行了数据扩增。弱化了各个参数（特征）之间的单一联系，使起作用的特征有更多组合，使从而模型不过分依赖某个特征。

5）提前停止训练，也就是减少训练的迭代次数。从上面的误差率曲线图可以看出，理论上能够找到一个训练程度，此时验证集误差率最低，视为拟合效果最好的点。

6）多模型投票方法，类似集成学习方法的思想，不同模型可能会从不同角度去拟合，互相之间取长补短，即使单独使用某个模型已出现过拟合，但综合起来却有可能减低过拟合程度，起到正则作用，提高了泛化效果。特别是使用多个非常简单的模型，更不容易产生过拟合。

 2、L1 L2正则化

　　L1 正则指在把参数的绝对值加到损失函数中，L2 正则化指把参数的L2范数（参数的平方值）加到损失函数中。下面从三种角度理解正则化。

　　2.1 先验分布

　　L1 相当于参数服从拉普拉斯分布，L2 参数服从高斯分布。

　　在最大似然估计中，假设权重w是未知参数，从而求得对数似然函数：

 

 

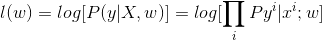
　　假设y_i 服从不同的概率分布，就能得到不同的模型。不妨假设y服从以下高斯分布

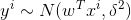
　　带入高斯分布的概率密度函数里，可得

　　

 

 

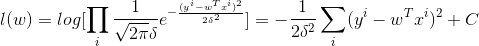
　　在最大后验概率估计中，讲权重w看出随机变量，也具有某种分布，从而有 

 

 

 

 

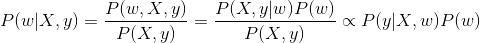
 　　从上面可以看出，最大后验概率是在最大似然估计的基础上增加了P(w),P(w)就是对权重系数w 的先验假设。

　　假设w服从高斯分布，则

　　

 

 

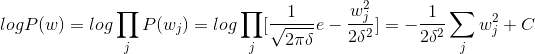
　　在w服从高斯分布下，logP(w)的效果相当于L2 正则，

　　若假设w服从拉普拉斯分布, 则

 

 

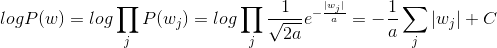
 　　在w服从高斯分布下，logP(w)的效果相当于L1 正则

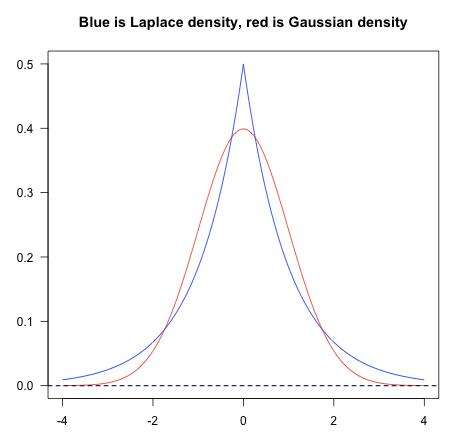
　　从先验分布的角度解释，为什么L1 稀疏，L2 平滑

　　看高斯分布，拉普拉斯分布的概率密度曲线就能看出，高斯分布，在0取值为0处相对平滑，拉普拉斯分布，在0处比较尖，取值为0 的概率

 

　　2.2 下降速度

　　

 

 

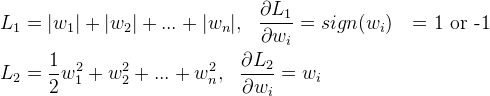
      L1 权值更新，每次减少一个固定的值,所以经过若干次迭代会会减到0，L2 随着w减小，更新减慢，所以L2会收敛到0 但不会等于0