Cards BZOJ 1004
Cards
【问题描述】
小春现在很清闲,面对书桌上的N张牌,他决定给每张染色,目前小春只有3种颜色:红色,蓝色,绿色.他询问Sun有多少种染色方案,Sun很快就给出了答案.进一步,小春要求染出Sr张红色,Sb张蓝色,Sg张绝色.他又询问有多少种方案,Sun想了一下,又给出了正确答案. 最后小春发明了M种不同的洗牌法,这里他又问Sun有多少种不同的染色方案.两种染色方法相同当且仅当其中一种可以通过任意的洗牌法(即可以使用多种洗牌法,而每种方法可以使用多次)洗成另一种.Sun发现这个问题有点难度,决定交给你,答案可能很大,只要求出答案除以P的余数(P为质数).
【输入格式】
第一行输入 5 个整数：Sr,Sb,Sg,m,p(m<=60,m+1<p<100)。n=Sr+Sb+Sg。接下来 m 行，每行描述一种洗牌法，每行有 n 个用空格隔开的整数 X1X2...Xn，恰为 1 到 n 的一个排列，表示使用这种洗牌法，第 i位变为原来的 Xi位的牌。输入数据保证任意多次洗牌都可用这 m种洗牌法中的一种代替，且对每种洗牌法，都存在一种洗牌法使得能回到原状态。
【输出格式】
不同染法除以P的余数
【样例输入】
1 1 1 2 7
2 3 1
3 1 2
【样例输出】
2
【样例解释】
有2种本质上不同的染色法RGB和RBG，使用洗牌法231一次可得GBR 和BGR，使用洗牌法312一次可得BRG和GRB。
【数据范围】
100%数据满足：Max{Sr,Sb,Sg}<=20。
题解：
Burnside引理：用D(ai)表示在置换ai下不变的元素个数。L表示本质不同的方案数。G表示置换群。|G|表示置换群的大小。
置换群简单地讲就是给定置换，所有置换的置换所组成的集合就是置换群
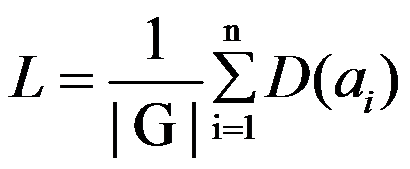
举个例子：
4个置换组成的置换群：
1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3
假设我们有2种颜色用0与1表示
第一种：所有方案都不变，D(a1) = 16
第二种：0000、1111，D(a2) = 2
第三种：0000、1111、0101、1010，D(a3) = 4
第四种：0000、1111，D(a4) = 2
那么 L = (16 + 2 + 4 + 2) / 4 = 6
这就是本质不同的方案数
题目中已经保证给出所有置换中，只要加上一个不变的置换就能得到置换群
显然置换可以拆成多个轮换相乘
所以对每种轮换内的元素进行同种颜色的染色，那么轮换中的颜色经过此置换仍然不变
那么用一个01背包，就可以求出在一个置换下不变的元素个数
然后有模数，所以用逆元求一下分母
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdlib>
5 #include<cstdio>
6 #include<cmath>
7 using namespace std;
8 inline int Get()
9 {
10 int x = 0;
11 char c = getchar();
12 while('0' > c || c > '9') c = getchar();
13 while('0' <= c && c <= '9')
14 {
15 x = (x << 3) + (x << 1) + c - '0';
16 c = getchar();
17 }
18 return x;
19 }
20 const int me = 123;
21 int r, b, g, m, p, n, t;
22 bool vis[me];
23 int a[me];
24 int si[me];
25 int num;
26 long long ans;
27 long long f[me][me][me];
28 inline long long Pow(long long x, int y)
29 {
30 long long res = 1;
31 long long sum = x % p;
32 while(y)
33 {
34 if(y & 1) res = (res * sum) % p;
35 sum = (sum * sum) % p;
36 y >>= 1;
37 }
38 return res;
39 }
40 int main()
41 {
42 r = Get(), b = Get(), g = Get(), m = Get(), p = Get();
43 n = r + b + g;
44 ++m;
45 t = m;
46 while(m--)
47 {
48 num = 0;
49 memset(f, 0, sizeof(f));
50 memset(si, 0, sizeof(si));
51 memset(vis, false, sizeof(vis));
52 for(int i = 1; i <= n; ++i)
53 {
54 if(m) a[i] = Get();
55 else a[i] = i;
56 }
57 for(int i = 1; i <= n; ++i)
58 {
59 if(!vis[i])
60 {
61 int c = a[i];
62 ++num;
63 while(!vis[c])
64 {
65 vis[c] = true;
66 ++si[num];
67 c = a[c];
68 }
69 }
70 }
71 f[0][0][0] = 1;
72 for(int i = 1; i <= num; ++i)
73 for(int j = r; j >= 0; --j)
74 for(int k = b; k >= 0; --k)
75 for(int l = g; l >= 0; --l)
76 {
77 if(j >= si[i]) f[j][k][l] = (f[j][k][l] + f[j - si[i]][k][l]) % p;
78 if(k >= si[i]) f[j][k][l] = (f[j][k][l] + f[j][k - si[i]][l]) % p;
79 if(l >= si[i]) f[j][k][l] = (f[j][k][l] + f[j][k][l - si[i]]) % p;
80 }
81 ans = (ans + f[r][b][g]) % p;
82 }
83 printf("%lld", (ans * Pow(t, p - 2)) % p);
84 }
