数学

1.裴蜀定理：

若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。

它的一个重要推论是：a,b互质的充分必要条件是存在整数x,y使ax+by=1.

 2.

a, b互质，a，b不能凑出的最大整数是a*b-a-b

 3.质数

试除法判断质数

时间复杂度： sqrt(n)

代码：

bool is_prime(int x)
{
　　if (x < 2) return false;
　　for (int i = 2; i <= x / i; i ++ )
　　　　if (x % i == 0)
　　　　　　return false;
　　return true;
}

质数筛：

 1 ~ n 中有 n / logn 个质数

埃氏筛：

void get_primes1(){

    for(int i=2;i<=n;i++){

        if(!st[i]){

            primes[cnt++]=i;

            for(int j=i;j<=n;j+=i) st[j]=true;//可以用质数就把所有的合数都筛掉；

        }

    }

}

线性筛：

void get_primes(){
    //外层从2~n迭代，因为这毕竟算的是1~n中质数的个数，而不是某个数是不是质数的判定
    for(int i=2;i<=n;i++){
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++){//primes[j]<=n/i:变形一下得到——primes[j]*i<=n,把大于n的合数都筛了就
        //没啥意义了
            st[primes[j]*i]=true;//用最小质因子去筛合数

            //1)当i%primes[j]!=0时,说明此时遍历到的primes[j]不是i的质因子，那么只可能是此时的primes[j]<i的
            //最小质因子,所以primes[j]*i的最小质因子就是primes[j];
            //2)当有i%primes[j]==0时,说明i的最小质因子是primes[j],因此primes[j]*i的最小质因子也就应该是
            //prime[j]，之后接着用st[primes[j+1]*i]=true去筛合数时，就不是用最小质因子去更新了,因为i有最小
            //质因子primes[j]<primes[j+1],此时的primes[j+1]不是primes[j+1]*i的最小质因子，此时就应该
            //退出循环，避免之后重复进行筛选。
            if(i%primes[j]==0) break;
        }
    }

}

矩阵快速幂：

快速幂：运算存在结合律时 可以把 a^n 拆成形如 a1 * a2 * a4 ....     O(logn)

求 (m^k)%p，时间复杂度 O(logk)。
int qmi(int m, int k, int p)
{
    int res = 1 % p, t = m;
    while (k)
    {
        if (k&1) res = res * t % p;
        t = t * t % p;
        k >>= 1;
    }
    return res;
}

矩阵快速幂求斐波那契数列

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 3;

int n, m;

void mul(int c[], int a[], int b[][N])
{
    int temp[N] = {0};
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j < N; j ++ )
            temp[i] = (temp[i] + (LL)a[j] * b[j][i]) % m;

    memcpy(c, temp, sizeof temp);
}

void mul(int c[][N], int a[][N], int b[][N])
{
    int temp[N][N] = {0};
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j < N; j ++ )
            for (int k = 0; k < N; k ++ )
                temp[i][j] = (temp[i][j] + (LL)a[i][k] * b[k][j]) % m;

    memcpy(c, temp, sizeof temp);
}

int main()
{
    cin >> n >> m;

    int f1[N] = {1, 1, 1};
    int a[N][N] = {
        {0, 1, 0},
        {1, 1, 1},
        {0, 0, 1}
    };

    n -- ;
    while (n)
    {
        if (n & 1) mul(f1, f1, a);  // res = res * a
        mul(a, a, a);  // a = a * a
        n >>= 1;
    }

    cout << f1[2] << endl;

    return 0;
}

高斯消元

用初等行变换 将 方程组变为上三角
1.把某一行乘一个非零的树
2.交换某两行
3.把某行若干倍加到另一行上去
A11 X1 + ............. + A1m Xn = B1
                A22 X2 ...+A2mXn = B2
                              ....................
                                       Xnn = Bn

1.完美阶梯型——有唯一解
2.非~ （1）0 = 非零 左无未知数右非零——无解
（2）0=0 ——无穷多解

高斯消元：
枚举每一列c
1.找到当前列绝对值最大的那一行
2.将这行换到最上面去
3.将该行第1个数变成1
4将下面所有行的当前列消成0

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 110;
const double eps = 1e-8;

int n;
double a[N][N];

int gauss()  // 高斯消元，答案存于a[i][n]中，0 <= i < n
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )  // 找绝对值最大的行
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);  // 将绝对值最大的行换到最顶端
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];  // 将当前行的首位变成1
        for (int i = r + 1; i < n; i ++ )  // 用当前行将下面所有的列消成0
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2; // 无解
        return 1; // 有无穷多组解
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];

    return 0; // 有唯一解
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n + 1; j ++ )
            scanf("%lf", &a[i][j]);

    int t = gauss();
    if (t == 2) puts("No solution");
    else if (t == 1) puts("Infinite group solutions");
    else
    {
        for (int i = 0; i < n; i ++ )
        {
            if (fabs(a[i][n]) < eps) a[i][n] = 0;  // 去掉输出 -0.00 的情况
            printf("%.2lf\n", a[i][n]);
        }
    }

    return 0;
}

 组合数学

 

卡特兰数

 

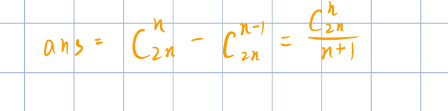
博弈论

公平组合游戏（ICG）：

1.两玩家交替行动

2.任意时刻可执行的合法性与那位玩家无关

3.不能行动的玩家判负

NIM∈ICG，但城建游戏，如围棋就不是

给定 n 堆石子，从中有a₁~a_n个石头，a₁^a₂^....a_n 若 = 0（先手必败）若 = x !=  0(先手必胜)

若 = x !=  0(先手必胜)

x  的二进制表示中最高 1 位在第 k 位。a₁~a_n 中必然有一个数 a_i 第 k 位是 1

则有 a_i^x < a_i^x ，所以可以从 a_i 中拿走 (a_i - a_i^x) 个石子 。a_i 变成 a_i^x 个石头

由 a₁^a₂^....a_{n =} x，变成 x^x = 0，使得当前局面变为必败局，交由下一名玩家操作。

 若 = 0 (先手必败）

设从 a_i  拿石头使之变为 a_i '可以使石子异或值 == 0

a₁^a₂^..a_i^..a_n  = 0  ①

a₁^a₂^..a_i'^..a_n = 0  ②

由假设得 ①^② =ai^ai' = 0 ^ 0 = 0

得出ai = ai'，所以无论怎么拿，都是必败态

SG函数

mex：找到集合中最小得不属于这个集合得自然数

若 x 局面可以到到达 y1，y2.....yk 局面

SG(X) = mex{SG(y1), SG(y2)...., SG(yk)}

SG(终点) = 0，到不了其他局面

SG(X) = 0(必败)，SG(X) != 0 (必胜)

任何非 0 状态可以走到 0 ，0 得状态走不到 0

如果有 n 个状态图，若 SG(x1) ^ SG(X2) ^ .... ^ SG(Xn) = 0（必败）!= 0 (必胜) 

 

若有环，游戏结束不了